算法沉淀——动态规划篇(子数组系列问题(上))
- 前言
- 一、最大子数组和
- 二、环形子数组的最大和
- 三、乘积最大子数组
- 四、乘积为正数的最长子数组长度
前言
几乎所有的动态规划问题大致可分为以下5个步骤,后续所有问题分析都将基于此
-
1.、状态表示:通常状态表示分为基本分为以下两种,其中更是以第一种为甚。
以i为结尾,dp[i] 表示什么,通常为代求问题(具体依题目而定)以i为开始,dp[i]表示什么,通常为代求问题(具体依题目而定)
-
2、状态转移方程
*以上述的dp[i]意义为以i位置为分界, 通过最近一步来分析和划分问题,由此来得到一个有关dp[i]的状态转移方程。 -
3、dp表创建,初始化
- 动态规划问题中,如果直接使用状态转移方程通常会伴随着
越界访问等风险,所以一般需要初始化。而初始化最重要的两个注意事项便是:保证后续结果正确,不受初始值影响;下标的映射关系。 - 而
初始化一般分为以下两种:直接初始化开头的几个值。一维空间大小+1,下标从1开始;二维增加一行/一列。
- 动态规划问题中,如果直接使用状态转移方程通常会伴随着
-
4、填dp表、填表顺序:根据状态转移方程来确定填表顺序。
-
5、确定返回值
一、最大子数组和
【题目链接】:53. 最大子数组和
【题目】:
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
&emdp;子数组是数组中的一个连续部分。
【示例】:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
【分析】:
我们可以定义dp[i]表示以i为结尾,最大连续子数组和。此时连续子数组长度分为1和大于1,分别对应如下情况:
- 如果dp[i-1]大于0,此时最大连续子数组和为dp[i-1] + nums[i]。长度大于1。
- 如果dp[i-1] <= 0,此时最大的连续子数组和就是nums[i]本身。长度为1.
所以我们可以得到状态转移方程为:dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1])。
但显然当i为0时,状态转移方程不适用。这里我们给出的方法时dp表空间额外增加1。同时为了保证在使用状态转移方程,新增空间对后续填表结果不产生印象。我们将dp[0]初始化为0即可。
【代码编写】:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n + 1);
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);
ret = max(ret, dp[i]);
}
return ret;
}
};
二、环形子数组的最大和
【题目链接】:918. 环形子数组的最大和
【题目】:
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
&emsp子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], …, nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
【示例】:
输入:nums = [5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
提示:
n == nums.length
1 <= n <= 3 * 104
-3 * 104 <= nums[i] <= 3 * 104
【分析】:
显然如果我们"死板"按照题目所说的环形数组进行分析,会感到无从下手。所以我们可以换一种思路:我们对数组被偷元素是否包含首尾,进行分类讨论。从而将环形数组问题转化称求普通子数组的最大和问题!
分类情况:
-
首位元素都被选,此时我们将原问题转化成求普通数组中子数组的最小和。最后用整个数组的和减去最小和,间接求出该情况最大值。
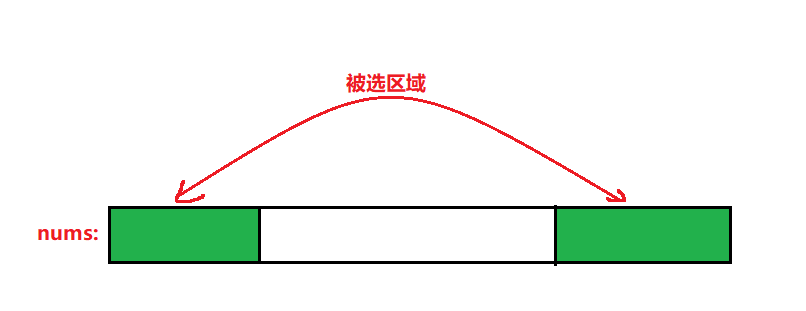
-
首位元素不全都被选。此时原问题转化成普通数组中子数组的最大和。
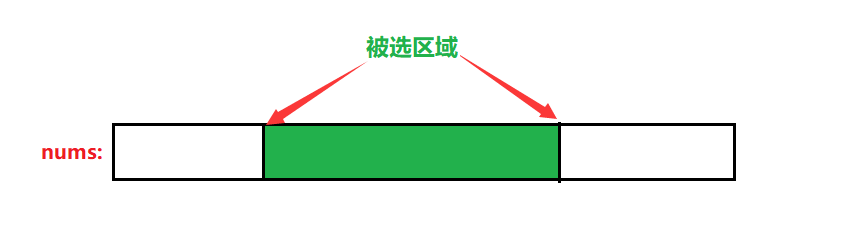
如何求普通数组最大子数组和、最小子数组和:
这里我们可以定义fi]表示以i位置为结尾的子数组最大和,g[i]表示以i位置为结尾的子数组最小和。
状态转移方程推导:
- 以i位置为结尾的子数组最大和分两种情况:如果f[i-1] >0, 此时最大子数组和为f[i-1] + nums[i]。否则最大子数组和为nums[i]本身。所以状态转移方程为:
f[i] = max(nums[i], dp[i-1] + nums[i])。 - 同理,以i位置为结尾的子数组最小和分两种情况:如果f[i-1] <0, 此时最小子数组和为f[i-1] + nums[i]。否则最小子数组和为nums[i]本身。所以状态转移方程为:
g[i] = min(g[i-1]+ nums[i], nums[i])
细节处理:
显然不管是求f[i]还是g[i],当i为0时,状态转移方程失效。这里各位办法是给f、g都额外新增一个空间。最后从左往右依次填表即可。
如果数组中元素全为负数时,此时子数组和最大值一定为负数。但此时我们发现g[i]最终求得的子数组最小和就是整个数组和,此时数组和减子数组最小和的最终结果为0。需要单独处理

【代码编写】:
class Solution {
public:
int maxSubarraySumCircular(vector<int>& nums) {
//数组和
int sum = 0;
for(auto x : nums)
{
sum += x;
}
int n = nums.size();
vector<int> f(n + 1);//普通数组最大连续子数组和
auto g = f;//普通数组最小连续子数组和
int fmax = INT_MIN, gmin = INT_MAX;//分别统计f中最大值,g中最小值
for(int i = 1; i <= n; i++)
{
f[i] = max(nums[i - 1], f[i - 1] + nums[i - 1]);
fmax = max(fmax, f[i]);
g[i] = min(nums[i - 1], g[i - 1] + nums[i - 1]);
gmin = min(gmin, g[i]);
}
return sum == gmin ? fmax : max(fmax, sum - gmin);//判断数组元素是否全为负数
}
};
三、乘积最大子数组
【题目链接】:152. 乘积最大子数组
【题目】:
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
&emsp测试用例的答案是一个 32-位 整数。
【示例】:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
【分析】:
我们可以定义f[i]表示以i为结尾的最大子数组乘积,g[i]表示以i为结尾的最小子数组乘积。
状态转移方程推导
-
以i为结尾的子数组长度可能为1,或大于1。对于大于1的情况,如果nums[i]>0,此时最大子数组乘积为g[i-1]*nums[i];如果nums[i]<0,此时最大子数组乘积为g[i-1]*nums[i]。我们仅需直接求得3种情况的最大值即可,即状态转移方程为:
f[i] = max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]))。
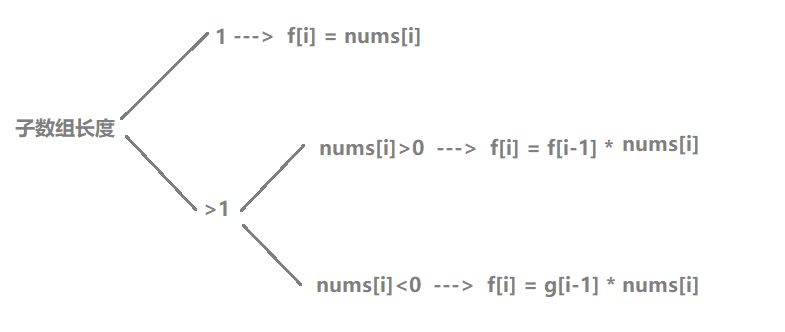
-
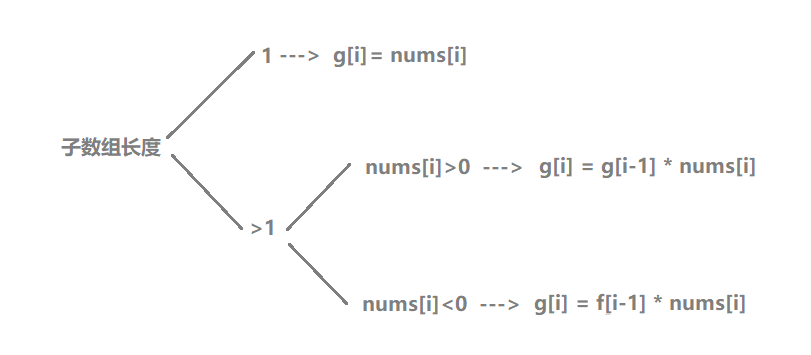
同理对于g[i]来说,也存在如下几种情况。最终可得状态转移方程为
g[i] = min(nums[i - 1], min(g[i - 1] * nums[i - 1], f[i - 1] * nums[i - 1]));
细节处理:
当i=0时,f、g的状态转移方程不适用。我们可以为f、g额外增加1个空间。同时为了防止新增结果对后续填表造成影响,我们将g[0]、f[0]初始化为1。
【代码编写】
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
vector<int> f(n + 1);//f[i]表示以i为结尾的子数组的最大乘积
auto g = f;//g[i]表示以i为结尾的子数组的最小乘积
int ret = INT_MIN;
f[0] = 1, g[0] = 1;
for(int i = 1; i <= n; i++)
{
f[i] = max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]));
g[i] = min(nums[i - 1], min(g[i - 1] * nums[i - 1], f[i - 1] * nums[i - 1]));
ret = max(ret, f[i]);
}
return ret;
}
};
四、乘积为正数的最长子数组长度
【题目链接】:1567. 乘积为正数的最长子数组长度
【题目】:
给你一个整数数组 nums ,请你求出乘积为正数的最长子数组的长度。一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。
请你返回乘积为正数的最长子数组长度。
【示例】:
输入:nums = [-1,-2,-3,0,1]
输出:2
解释:乘积为正数的最长子数组是 [-1,-2] 或者 [-2,-3] 。
【分析】:
我们定义f[i]表示以i为结尾,乘积为正的子数组最长长度;g[i]表示以i为结尾,乘积为负的子数组最长长度。
状态转移方程推导:
我们可以从最后一个元素nums[i[入手,此时分为以下几种情况:
- 最长子数组长度可能为1,或大于1,具体如下:
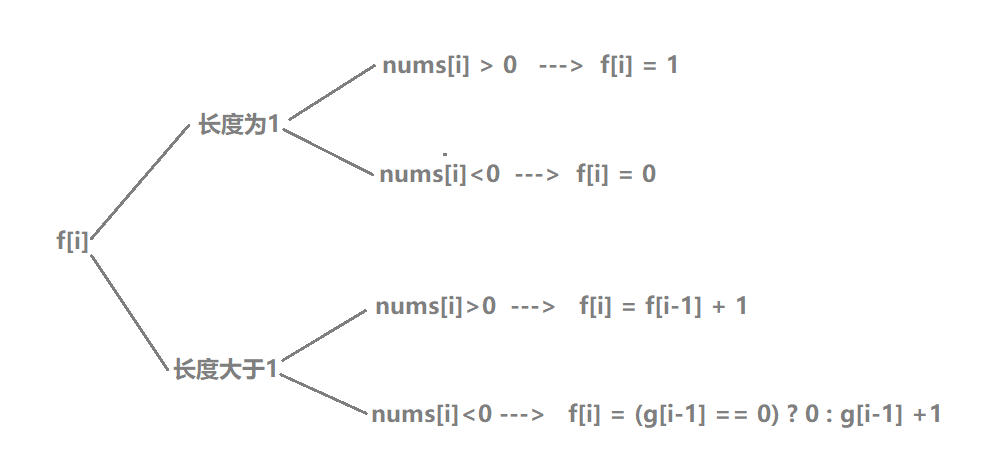
将上述情况仅需合并后,可得:
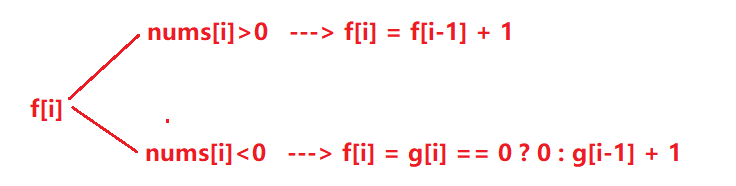
- 同理,g[i]的情况如下:
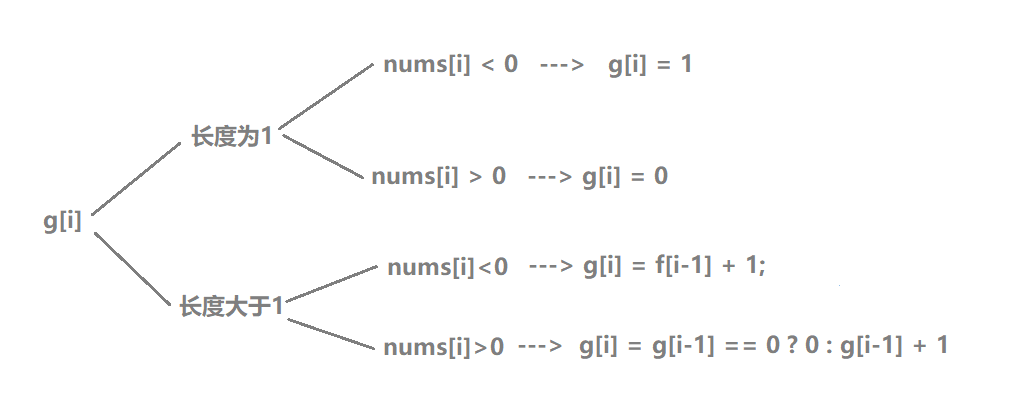
合并后,可得:

细节处理:
显然当i为0时,f、g的状态转移方程都失效。所以我们给f、g额外增加一个空间。为了保证新增空间对后续填表结果不造成印象,我们将f[0]、g[0]初始化为0。最后从左往右填表即可。
【代码编写】:
class Solution {
public:
int getMaxLen(vector<int>& nums) {
int n = nums.size();
vector<int> f(n + 1);//f[i]: 以i为结尾的,乘积为正的最长子数组长度
auto g = f;//g[i]: 以i为结尾的,乘积为负的最长子数组长度
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
if(nums[i - 1] > 0)
{
f[i] = f[i - 1] + 1;
g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
}
else if(nums[i - 1] < 0)
{
f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
g[i] = f[i - 1] + 1;
}
ret = max(ret, f[i]);
}
return ret;
}
};