算法学习17:背包问题(动态规划)
文章目录
- 算法学习17:背包问题(动态规划)
- 前言
- 一、01背包问题:
- 1.朴素版:(二维)
- 2.优化版:(一维)
- 二、完全背包
- 1.朴素版:(3重for)
- 2.稍微优化版:(二维)
- 3.完全背包问题模版:(最终优化版)
- 三、多重背包
- 1.朴素版:()
- 2.多重背包问题的“二进制优化”:
- 四、分组背包
- 在这里插入图片描述
- 总结
前言

提示:以下是本篇文章正文内容:
一、01背包问题:
1.朴素版:(二维)
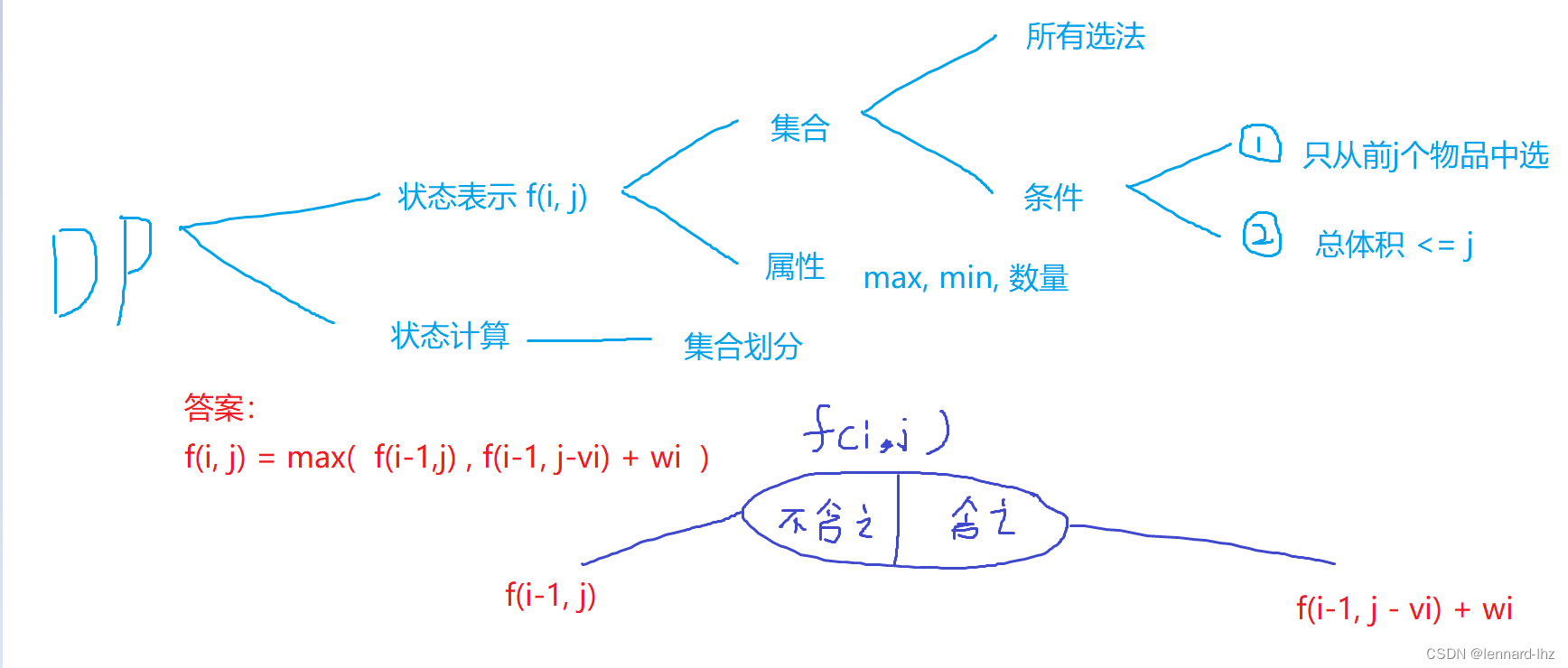

// 例题:有n件物品,和一个容量是m的背包,每件物品只能使用一次。
// 第i件物品的体积是vi,价值是wi,
// 求将哪些物品装入背包,可以使总价值最大。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];// v:体积, w:价值
int f[N][N];// 从前i件物品中取,放到容量为j的背包中,最大的价值。
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= m; j ++)
{
f[i][j] = f[i - 1][j];// 不取
if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);// 取
}
cout << f[n][m] << endl;
return 0;
}
2.优化版:(一维)
// 优化版:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];// v:体积, w:价值
int f[N];// 从i件物品中去,放到容量为j的背包,最大的价值。
// 注意要执行i轮循环
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
// 注意1:如果这里不是倒着遍历,那么可能存在,在前面的时候,i物品已经被放进背包了
// 从大到小,保证前面的“状态”,还没有更新过。
for(int j = m; j >= v[i]; j --)
// 不取 和 取
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
二、完全背包
1.朴素版:(3重for)
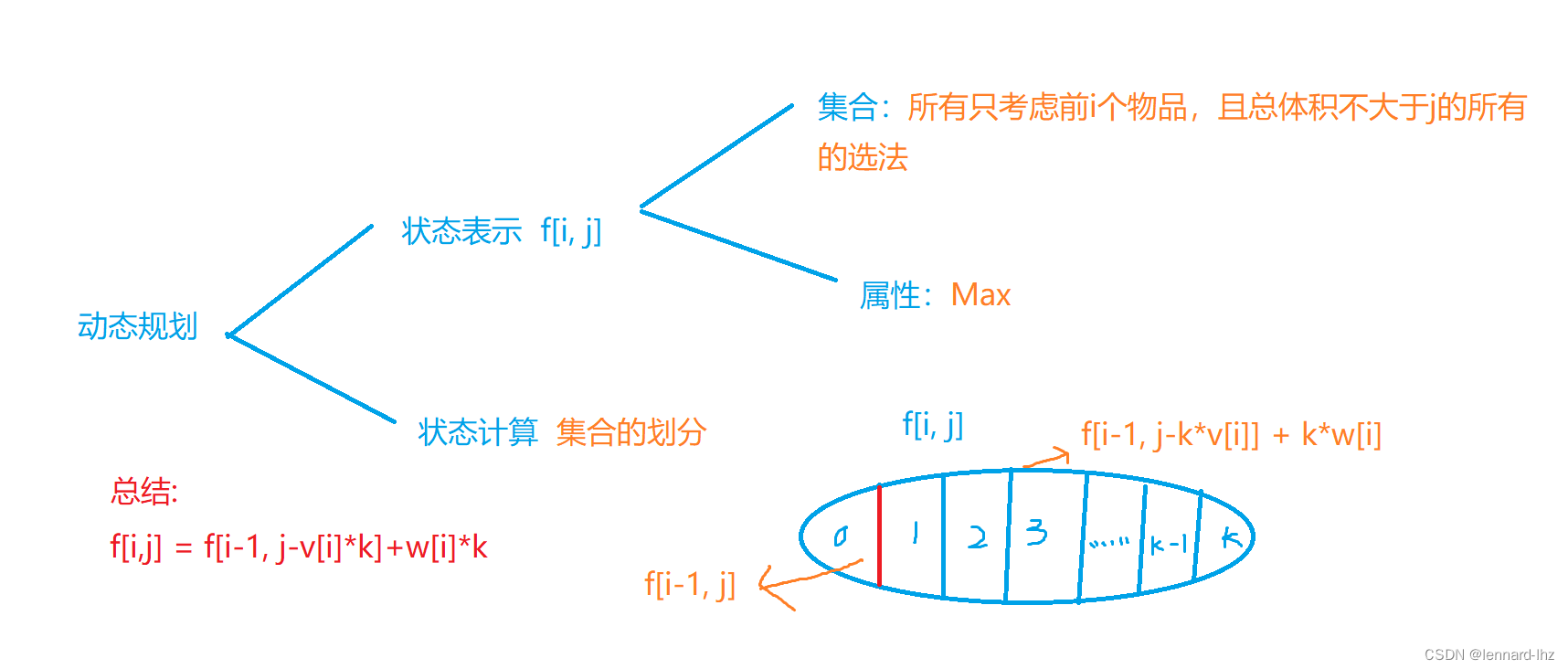
// 例题:有n种物品,容量为m的背包,“每种物品都有无限件可用”。
// 第i件物品的体积是vi,价值是wi,
// 求将哪些物品装入背包,可以使总价值最大,输出最大价值。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
// 3重for循环:
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= m; j ++)
for(int k = 0; k * v[i] <= j; k ++)
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
return 0;
}
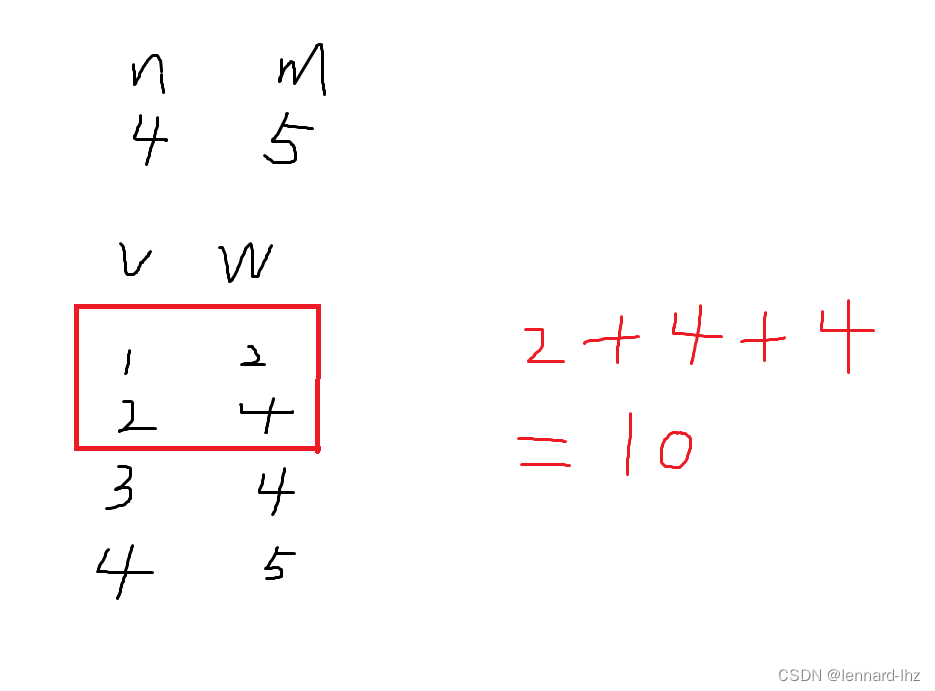
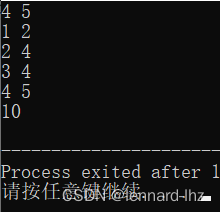
2.稍微优化版:(二维)

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= m; j ++)
{
// 这样就和01背包问题有点像了
// 不同的是:f[i - 1][j - v[i]] + w[i]
f[i][j] = f[i - 1][j];
// 注意1:要加一个判断条件 (否者越界)
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
3.完全背包问题模版:(最终优化版)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
// 为什么是从前往后遍历,因为每件物品可以使用无限次,不存在重复问题
for(int j = v[i]; j <= m; j ++)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m]<< endl;
return 0;
}
三、多重背包
1.朴素版:()
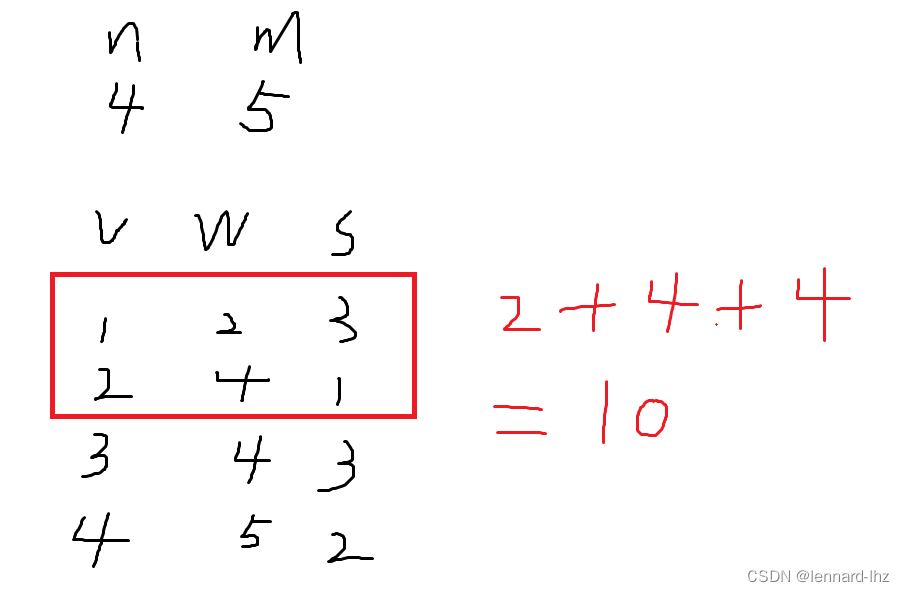
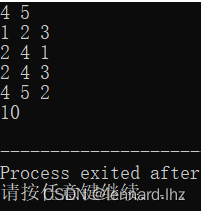
2.多重背包问题的“二进制优化”:

/*
多重背包问题的“二进制优化”:
请先记住:二进制数的组合可以表示一个0~s范围内的十进制数
那么我们将总数量为s的一个“大包裹”转换为“1 2 4 8 16 32 64 .......”这样的小包裹
然后对于:这些小包裹,我们选择“取或者不取”,这样就把“多重背包问题”转换为“01背包问题”
*/
/*
注意:为什么要优化?
第一种也可以使用,但是当数据范围大的时候就是出现Time Limit Exceed问题。
(1)0< n, m <100 0< vi, wi, si <100
(2)0 < n <1000 0 < m < 2000 0 < vi, wi, si <2000
const int N = 25000 是如何得到的?1000 * log2(2000) = 1000 * 11 = 22000
*/
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 25000, M = 2010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
int cnt = 0;// 标记 :作为打包后的总数量
for(int i = 1; i <= n; i ++)
{
int a, b, s;// 体积,容量,数量
cin >> a >> b >> s;
int k = 1;
while(k <= s)
{
cnt ++;
v[cnt] = a * k;// 打包后的体积
w[cnt] = b * k;// 打包后的容量
s -= k;// 剩余的总数量
k *= 2;// 打包的件数
}
if(s > 0)// 多了
{
cnt ++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;// 打包后的所有包裹的数量
// 此时,又相当于01背包问题
for(int i = 1; i <= n; i ++)
for(int j = m; j >= v[i]; j --)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
四、分组背包
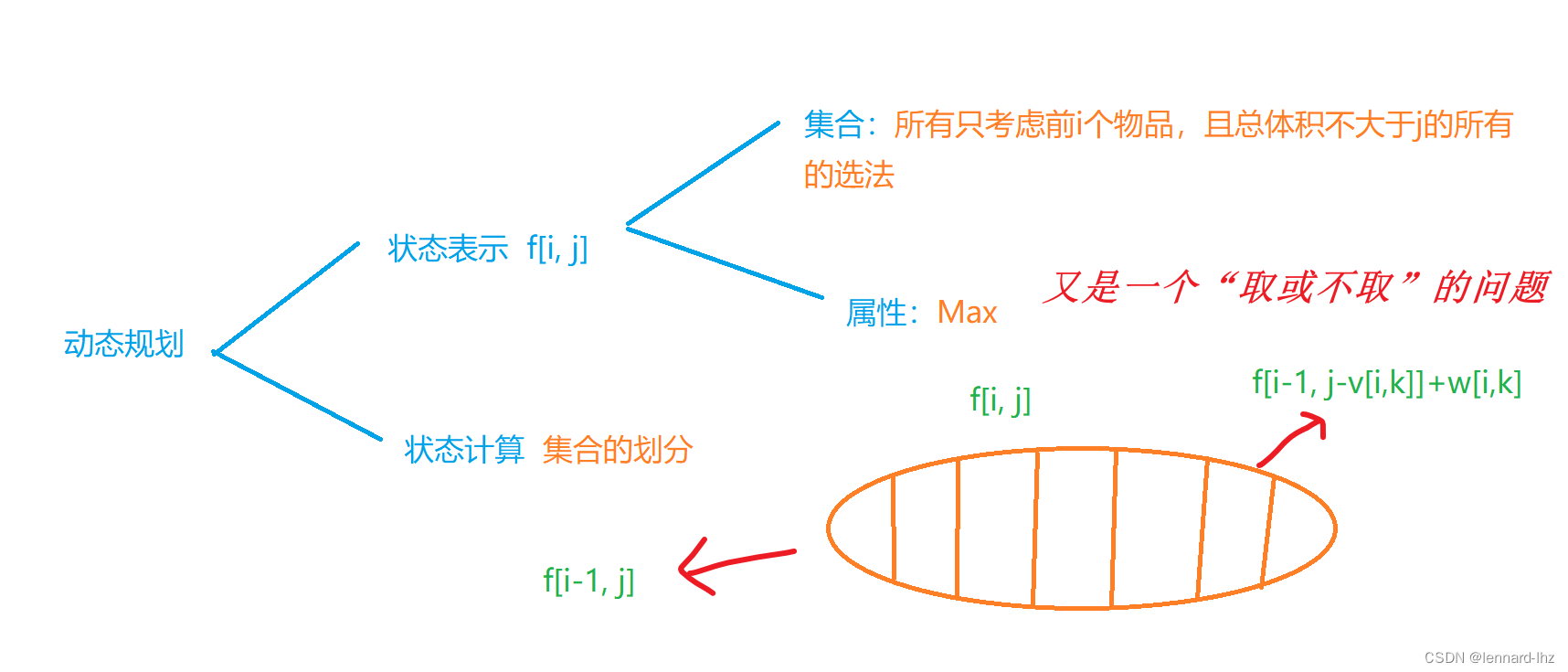

// 有n组物品,容量为m的背包,
// 每组物品有若干个,同一组内的物品最多只能选一个
// 每件物品的体积是vij,价值是wij,其中i是组号,j是组内编号
// 求将哪些物品装入背包,可以使总价值最大,输出最大价值。
/*
输入:n,m
接下来n组数据:
第一行:s表示这一组物品的数量
接下来s行:v,w
*/
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
{
cin >> s[i];
for(int j = 0; j <s[i]; j ++)
cin >> v[i][j] >> w[i][j];
}
for(int i = 1; i <= n; i ++)
// 像01背包:“取或不取”,只有一件,不可以重复,那么就倒着遍历,保证前面是未更新的
for(int j = m; j >= 0; j --)
for(int k = 0; k < s[i]; k ++)
if(v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}
总结
提示:这里对文章进行总结:
💕💕💕