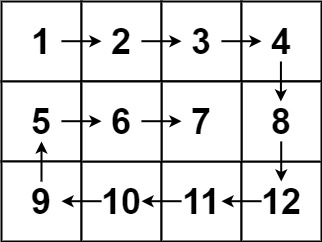

还是一道比较明显的求
LCA(最近公共祖先)模型的题目,我们可以使用多种方法来解决该问题,这里我们使用更好写的离线的tarjan算法来解决该问题。
除去tarjan算法必用的基础数组,我们还有一个数组d[],d[i]记录的是每个点的出度,也就是它的延迟时间,以及数组w[],w[i]的含义是点i到根节点的延迟时间。在通过dfs求出每个点i的w[i]以后,在tarjan中我们该如何求出两点的延迟时间呢?
我们设点i到j的延迟时间为f(x),当我们求得i与j的最近公共祖先为anc,我们首先让f(x)=w[i]+w[j]
但很明显,我们多加了两w[anc],所以我们需要减去两倍的w[anc]
但延迟时间还包括经过anc的时间,所以还得加上一个d[anc]。此处请结合w[]和d[]的含义理解。
最后能得出式子:f(x)=w[i]+w[h]−w[anc]2+d[anc]
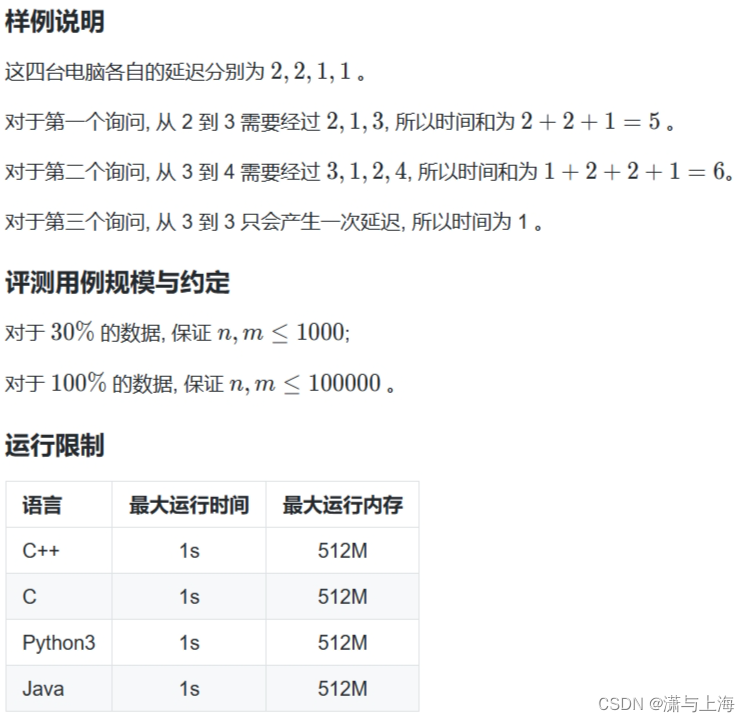
我们利用这个式子在tarjan函数中就能得出每个询问的答案,当然对于起始和结束都在同一个节点的情况下,它的答案就是当前节点的出度,我们可以进行特判一下。输入输出较多,建议使用scanf和printf进行输入输出。
时间复杂度:dfs:每个点遍历一次,复杂度级别O(n),tarjan算法复杂度接近 O(n+m)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N=100010;
unordered_map<int,vector<int>> gra;
int n,m;
//单个点的出度
int d[N];
//记录点i到根节点的延迟
int w[N];
//并查集数组
int q[N];
//记录答案
int res[N];
int st[N];
//存下查询
vector<PII> query[N];
//并查集查询
int find(int x){
if(x!=q[x]) q[x]=find(q[x]);
return q[x];
}
void dfs(int u,int fa)
{
w[u]+=d[u];
for(auto g:gra[u]){
if(g==fa) continue;
w[g]+=w[u];
dfs(g,u);
}
}
void tarjan(int u)
{
st[u]=1;
for(auto j:gra[u]){
if(!st[j])
{
tarjan(j);
q[j]=u;
}
}
for(auto item: query[u]){
int y=item.first,id=item.second;
if(st[y]==2){
int anc=find(y);
res[id]=w[y]+w[u]-w[anc]*2+d[anc];
}
}
st[u]=2;
}
int main()
{
cin>>n>>m;
for(int i=0;i<n-1;++i){
int a,b;
scanf("%d%d",&a,&b);
gra[a].push_back(b);
gra[b].push_back(a);
d[a]++,d[b]++;
}
for(int i=0;i<m;++i){
int a,b;
scanf("%d%d",&a,&b);
if(a!=b){
query[a].push_back({b,i});
query[b].push_back({a,i});
}else{
res[i]=d[a];
}
}
dfs(1,-1);
for(int i=1;i<=n;++i) q[i]=i;
tarjan(1);
for(int i=0;i<m;++i) printf("%d\n",res[i]);
return 0;
}
错误答案:用floyd直接爆炸
错误答案
#include<bits/stdc++.h>
using namespace std;
const int N=1005,M=1005;
int deg[N];//度
int dis[N][N];
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
memset(dis,0x7f,sizeof(dis));
int n,m;cin>>n>>m;int v1,v2;
for(int i=1;i<n;++i){
cin>>v1>>v2;
++deg[v1];++deg[v2];
}
for(int i=1;i<n;++i){
dis[v1][v2]=deg[v1];
dis[v2][v1]=deg[v2];
}
for(int k=1;k<=n;k++)for(int v1=1;v1<=n;v1++)for(int v2=1;v2<=n;v2++)//枚举点
if((v1!=k)&&(v2!=k)&&(v1!=v2))
dis[v1][v2]=min(dis[v1][v2],dis[v1][k]+dis[k][v2]);
int start,end;
while(m--){
cin>>start>>end;
cout<<dis[start][end]+deg[end];
}
return 0;
}
/*
4 3
1 2
1 3
2 4
2 3
3 4
3 3
*/