LeetCode题练习与总结：螺旋矩阵

news2024/11/26 14:51:05

一、题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

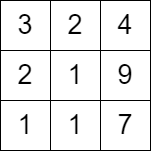
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

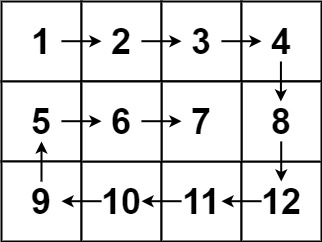
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

二、解题思路

初始化一个空列表用于存储最终的螺旋顺序元素。
定义四个方向：右、下、左、上，分别对应行增加、列增加、行减少、列减少。
使用一个循环，直到矩阵中所有元素都被访问过。
在每次循环开始时，从当前层的左上角开始，按照右-下-左-上的顺序遍历该层的所有元素，并将它们添加到结果列表中。
每遍历完一层，就将下一层的边界缩小，即上边界下移，下边界上移，左边界右移，右边界左移。
重复步骤4和5，直到所有元素都被访问。

三、具体代码

import java.util.ArrayList;
import java.util.List;

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> result = new ArrayList<>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return result;
        }

        int rows = matrix.length;
        int cols = matrix[0].length;
        int top = 0, bottom = rows - 1, left = 0, right = cols - 1;

        while (top <= bottom && left <= right) {
            // 从左到右遍历上层
            for (int i = left; i <= right; i++) {
                result.add(matrix[top][i]);
            }
            top++;

            // 从上到下遍历右侧
            for (int i = top; i <= bottom; i++) {
                result.add(matrix[i][right]);
            }
            right--;

            // 从右到左遍历下层
            if (top <= bottom) {
                for (int i = right; i >= left; i--) {
                    result.add(matrix[bottom][i]);
                }
                bottom--;
            }

            // 从下到上遍历左侧
            if (left <= right) {
                for (int i = bottom; i >= top; i--) {
                    result.add(matrix[i][left]);
                }
                left++;
            }
        }

        return result;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

代码中的主要操作是一个 while 循环，该循环会遍历矩阵的每个元素恰好一次。
由于矩阵有 rows 行和 cols 列，总的元素数量是 rows * cols。
因此，while 循环的迭代次数是 rows * cols，这意味着代码的时间复杂度是 O(rows * cols)，或者说是 O(N)，其中 N 是矩阵中的元素总数。

2. 空间复杂度

代码中使用了一个结果列表 result 来存储所有的输出元素。
这个列表在最坏的情况下（即当所有的元素都被访问时）将包含 rows * cols 个元素。
此外，代码中使用了固定数量的变量（top, bottom, left, right），这些变量的空间需求不随输入矩阵的大小而变化。
因此，代码的空间复杂度是 O(rows * cols)，或者说是 O(N)，其中 N 是矩阵中的元素总数。

五、总结知识点

二维数组（Matrix）：代码处理的是一个二维数组（int[][] matrix），这是存储和操作矩阵数据的基本数据结构。
边界检查：在进行螺旋遍历之前，代码首先检查矩阵是否为空或者行列数是否为0，这是为了避免数组越界异常（ArrayIndexOutOfBoundsException）。
循环控制：使用 while 循环来控制螺旋遍历的过程，循环条件 top <= bottom && left <= right 确保了当矩阵的所有边界都遍历过之后才结束循环。
四个方向的遍历：螺旋遍历涉及四个方向的移动，分别是从左到右、从上到下、从右到左、从下到上。代码中通过嵌套的 for 循环来实现这四个方向的遍历。
边界更新：在每次完成一个方向的遍历后，需要更新边界变量 top, bottom, left, right，以便在下一次循环中遍历下一层的元素。
结果列表（ArrayList）：使用 ArrayList 来存储遍历过程中收集的元素。ArrayList 是 Java 中的一个动态数组，可以动态地增长和缩小，适合在未知数量的元素集合中使用。
集合操作：代码中使用了 List 接口的 add 方法来向 ArrayList 中添加元素。
递归结构：虽然代码本身没有使用递归，但螺旋遍历的过程本质上是一种递归结构，每一层的遍历都可以看作是对下一层的递归调用。