前言:
周五晚上的训练赛,以后应该每两周都会有一次。
正文:
Problem:A矩阵翻转:

#include<bits/stdc++.h>
using namespace std;
int a[55][55];
int main(){
int n,m;
while(cin>>n>>m){
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int j=1;j<=m;j++){
for(int i=n;i>=1;i--){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
}
return 0;
} 用二维数组模拟矩阵。
Problem:B守夜人的游戏:

#include<bits/stdc++.h>
using namespace std;
int a[25];
int main(){
int n;
while(cin>>n){
long long ans=0;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
long long x=a[i];
ans=max(x,ans);
for(int j=i+1;j<=n;j++){
x*=a[j];
ans=max(x,ans);
}
}
cout<<ans<<endl;
}
}暴力即可,注意答案要开long long不然会暴int。
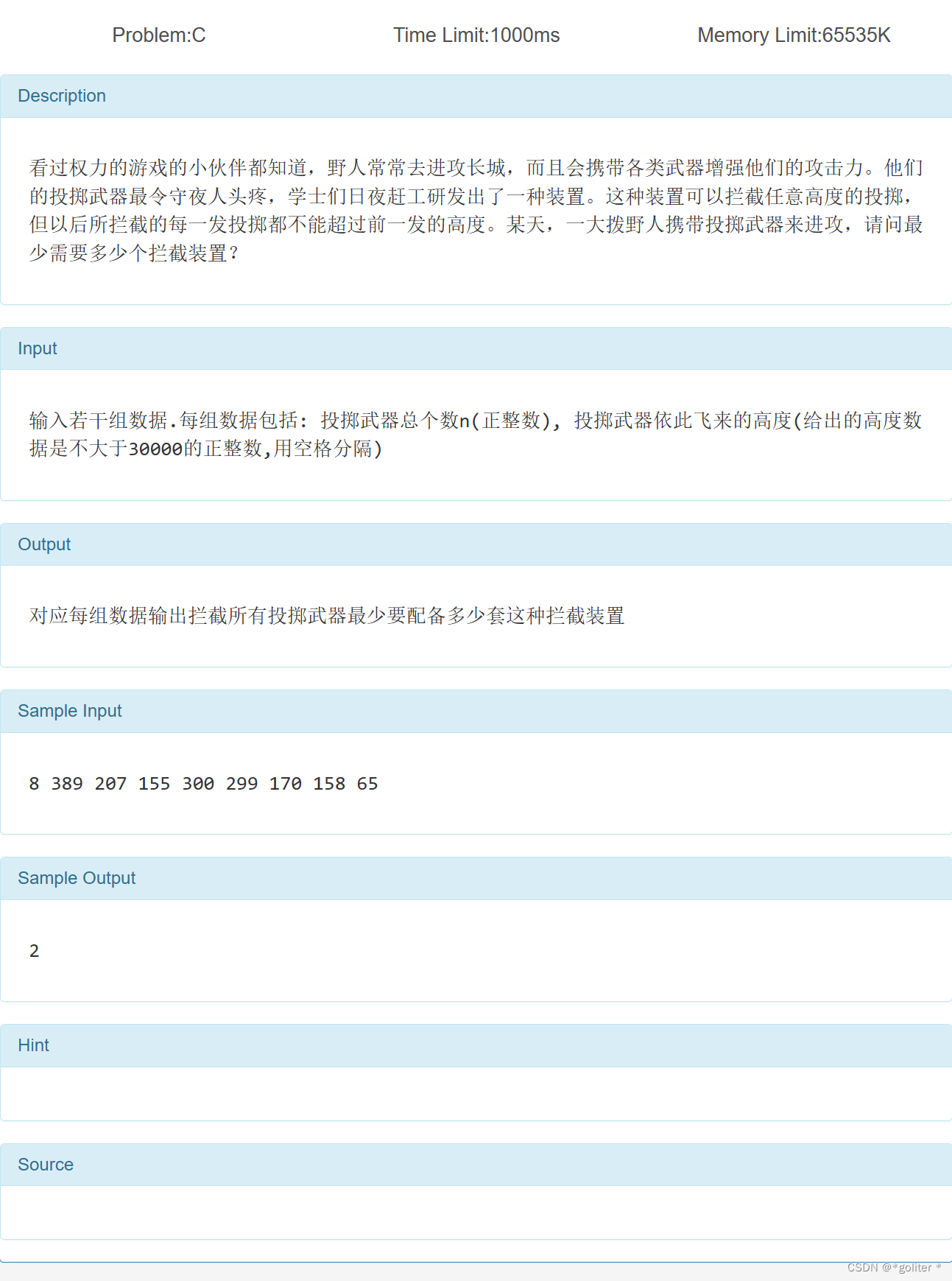
Problem:C野人来袭:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int a[N],book[N];
int main(){
long long n;
while(cin>>n){\
memset(book,0,sizeof(book));
int ans=0;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
int s=0;
if(book[i]==0){
book[i]=1;s=a[i];ans++;
for(int j=i+1;j<=n;j++){
if(book[j]==0&&s>=a[j]){
book[j]=1;s=a[j];
}
}
}
}
cout<<ans<<endl;
}
return 0;
}写这道题前我们先要搞清这道题的意思。题目中的拦截装置的高度在来拦截投来的武器后会变为这个武器高度(开始相当于无穷大),那么这个装置就无法再拦截更高的武器了,我们就需要第二个拦截装置,以此类推,我们就可以计算出装置的数量。又由装置的先后性我们可以知道所有武器中能被第一个装置拦截那么就一定不会被第二个装置拦截。那么我们先假设有n个装置,先对第一个装置分析,从第一个未拦截的武器开始,标记他可以依次序的拦截下武器(遍历数组找一串递减数列),再从第二个装置分析,从第一次标记后第一个未标记的武器开始,继续下去直至所有武器都被标记,这样就找出了答案。
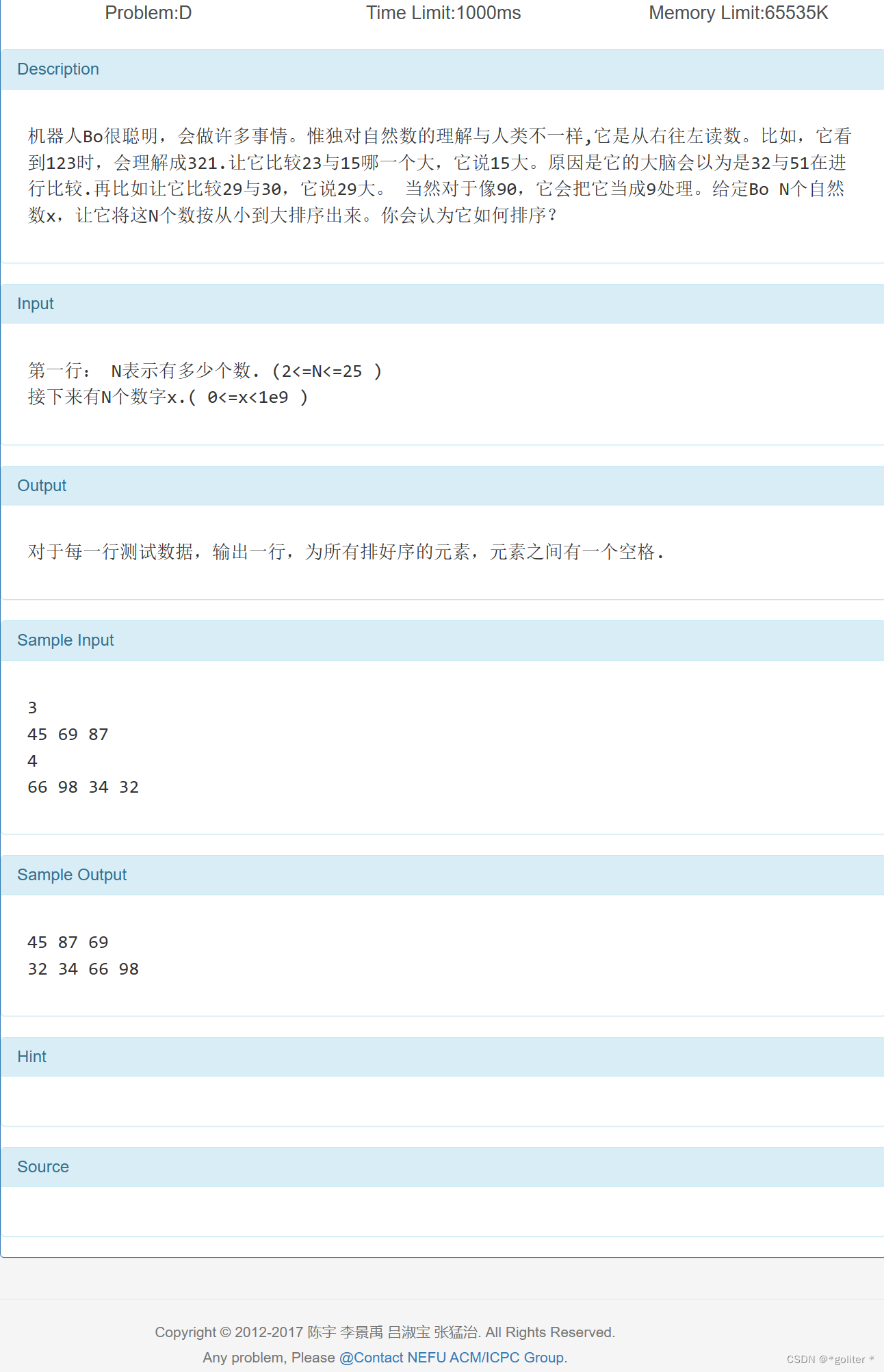
Problem:D机器人:
#include<bits/stdc++.h>
using namespace std;
typedef struct num{
int t,r;
}robot;
robot a[30];
bool cmp(robot j,robot k){
return j.r<=k.r;
}
int rev(int x){
int d[10];
int ans=0;
int p=1;
while(x){
d[p]=x%10;
x/=10;
p++;
}
for(int i=p-1;i>=1;i--){
ans+=d[i]*pow(10,p-i-1);
}
return ans;
}
int main(){
int n;
while(cin>>n){
for(int i=1;i<=n;i++){
cin>>a[i].t;
a[i].r=rev(a[i].t);
}
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++){
cout<<a[i].t;
if(i!=n)cout<<" ";
}
cout<<endl;
}
return 0;
}写一个反转数字的函数,在定义一个由数和它的反转数构成的结构体,写一个比较函数,排序后输出即可。
Problem:F美丽的黄山:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,a[100000],ans=0,max;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
if(i==1){
max=a[i];
ans++;}
else{if(max<a[i]){
max=a[i];
ans++;
}
}
}
cout<<ans;
return 0;
}之前写过的题,见2023年林大(东北林业大学)ACM校赛大一组 个人题解(已完成)_python程序设计与问题求解东北林业大学-CSDN博客
Problem:E点的运动:

#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
while(n--){
double x1,x2,y1,y2,x0,y0,vx,vy,t,ti,tj,tk,tl;
cin>>x1>>y1>>x2>>y2>>x0>>y0>>vx>>vy>>t;
//一般情况
if(vx!=0&&vy!=0){
ti=(x1-x0)/vx,tj=(x2-x0)/vx,tk=(y1-y0)/vy,tl=(y2-y0)/vy;
//无论t取何值都无法经过
if(max(ti,tj)<min(tk,tl)||max(tk,tl)<min(ti,tj)){
cout<<"NO"<<endl;
continue;
}
//存在t值使它能经过
int flag=0;
if(y0+vy*ti<=y1&&y0+vy*ti>=y2&&ti>=0&&ti<=t)flag=1;
if(y0+vy*tj<=y1&&y0+vy*tj>=y2&&tj>=0&&tj<=t)flag=1;
if(x0+vx*tk<=x2&&x0+vx*tk>=x1&&tk>=0&&tk<=t)flag=1;
if(x0+vx*tl<=x2&&x0+vx*tl>=x1&&tl>=0&&tl<=t)flag=1;
if(flag){
cout<<"YES"<<endl;
continue;
}
else{
cout<<"NO"<<endl;
continue;
}
}
//特判vx与vy都为0的情况
if(vx==0&&vy==0){
if((x0==x1||x0==x2)&&y0>=y2&&y0<=y1){
cout<<"YES"<<endl;
continue;
}
else if((y0==y1||y0==y2)&&x0>=x1&&x0<=x2){
cout<<"YES"<<endl;
continue;
}
else{
cout<<"NO"<<endl;
continue;
}
}
//分别判断vx=0与vy=0的情况
if(vx==0){
if(x0<x1||x0>x2){
cout<<"NO"<<endl;
continue;
}
else{
tk=(y1-y0)/vy,tl=(y2-y0)/vy;
if(min(tk,tl)>=0&&min(tk,tl)<=t){
cout<<"YES"<<endl;
continue;
}
else{
cout<<"NO"<<endl;
continue;
}
}
}
if(vy==0){
if(y0<y2||y0>y1){
cout<<"NO"<<endl;
continue;
}
else{
ti=(x1-x0)/vx,tj=(x2-x0)/vx;
if(min(ti,tj)>=0&&min(ti,tj)<=t){
cout<<"YES"<<endl;
continue;
}
else{
cout<<"NO"<<endl;
continue;
}
}
}
}
return 0;
}重量级选手,这题需要用到一些平面几何的知识。见下
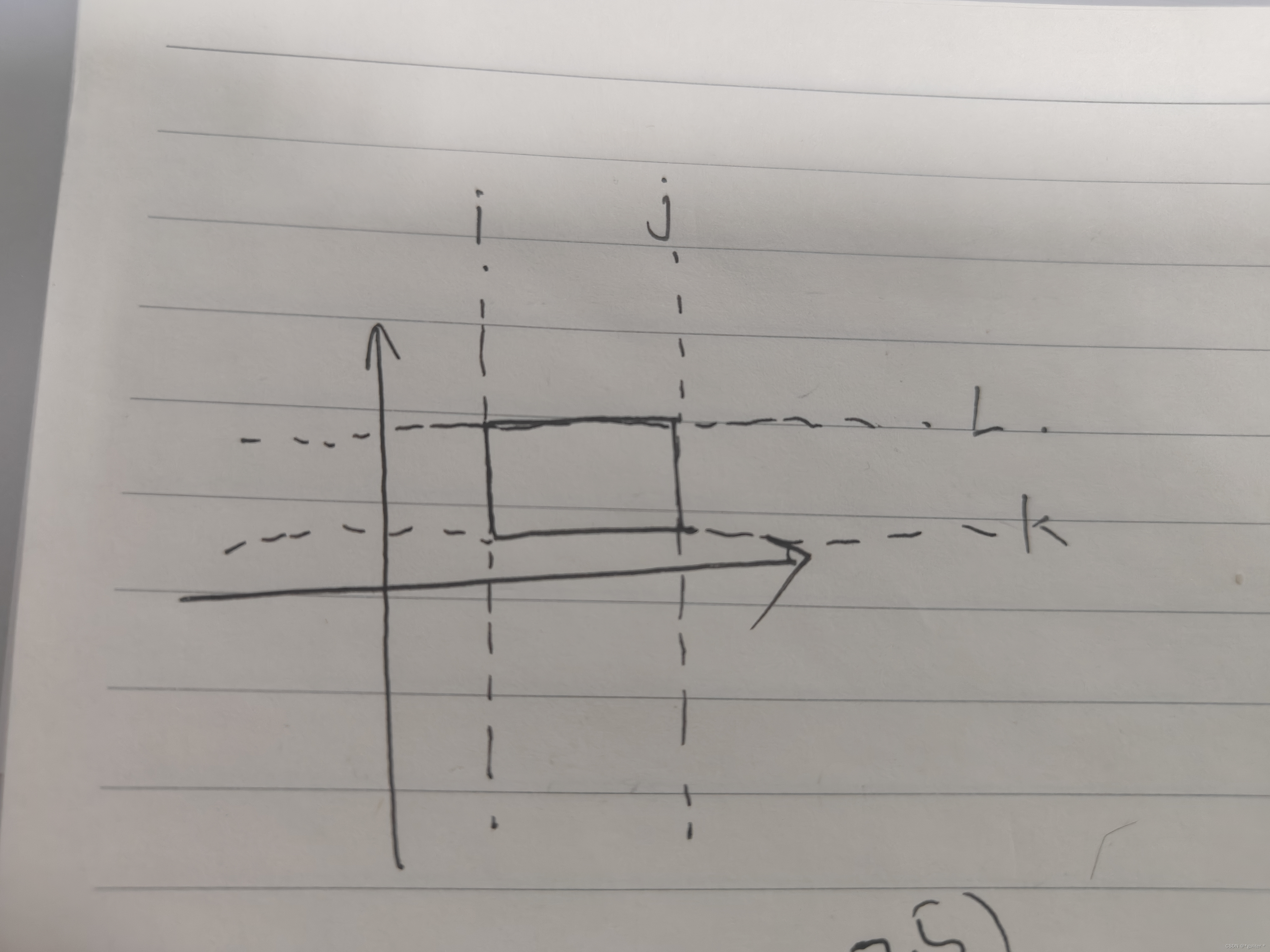
对于一个点来说,如果他前进方向上的直线经过i,j,k,l这四条直线的次序是横横竖竖或竖竖横横(i,j为竖,k,l为横),那么这条直线永远无法经过这个矩形(可以自己画图试一下),那么我们就可以从起点开始,计算出到达i,j,k,l的时间,判断i,j,k,l经过的次序。剩下的情况就需要根据t的大小来判断经过矩形的时间是否合法。注意要特判vx=0或vy=0以及都为0的情况。
补充:如果点在矩形内但没经过边的话不算经过(我又交了一遍代码尝试过了)
后记:
欢迎大家来讨论、相互学习。