目录

1 主要内容

日前计划模型

日内调整模型

不确定集建模

2 部分代码

3 程序结果

4 下载链接

---

1 主要内容

该程序复现文章《计及需求侧响应日前—日内两阶段鲁棒备用优化》，以6节点系统为例，综合考虑风电出力不确定性与电力设备 N-k强迫停运，增强电力系统应对不确定性因素的鲁棒性。基于鲁棒模型对系统运行备用进行优化，最小化电网在最恶劣运行场景下的调整成本，保证电网的安全可靠运行,并采用列和约束生成算法对两阶段三层优化问题进行求解。这个程序算是个超级丐版，注释较少，运行结果也少，如果预算充足可以参考一文说清楚6节点电网两阶段鲁棒优化调度如何编程，同时附赠【KKTCCG】IEEE6节点系统两阶段鲁棒优化调度matlab，学起来更加便捷轻松！

• 日前计划模型

• 日内调整模型

• 不确定集建模

2 部分代码

%风电场接在母线5上，在风电场端口集成储能系统
%118系统风电场接在母线19、25、40、62
​
%% 数据及常数矩阵
mpc=loadcase('case6ww');
bus=mpc.bus;
branch=mpc.branch;
gen=mpc.gen;
gencost=mpc.gencost;
baseMVA=mpc.baseMVA;
​
load('data.mat');
CPw=Cw(:,1:24,3)*300;%修改风电场场景、时间间隔、数目与容量
CPw=permute(CPw,[3,2,1]);
LD=1.8*bus(:,3)*Load(:,1:24);%修改Load,以改变考虑的时间间隔
​
NB=size(bus,1);
NG=size(gen,1);
NL=size(branch,1);
NW=size(CPw,1);
NT=size(CPw,2);
NS=size(CPw,3);
​
dW=zeros(NW,NT,NS);
maxdW=zeros(NW,NT);
mindW=zeros(NW,NT);
for i=1:NS
    dW(:,:,i)=CPw(:,:,i)-CPw(:,:,1);
end
for i=1:NW
    for j=1:NT
        maxdW(i,j)=1.2*max(dW(i,j,:));
        mindW(i,j)=1.2*min(dW(i,j,:));
    end
end
​
X=repmat(branch(:,4),1,NT);
Fmax=repmat(branch(:,6),1,NT);
PGmax=repmat(gen(:,9),1,NT);
PGmin=0.85*repmat(gen(:,10),1,NT);
LIDRmax=0.4;
% LIDRmax=0.1;
Pt=gen(:,10);%修改爬坡约束
​
ref=find(bus(:,2)==3);
G2B=zeros(NB,NG);
for i=1:NG
    G2B(gen(i,1),i)=1;
end
W2B=zeros(NB,NW);
W2B(5,1)=1;
B2B=zeros(NB,NL);
for i=1:NL
    B2B(branch(i,1),i)=1;
    B2B(branch(i,2),i)=-1;
end
​
costa=gencost(:,5);
costb=gencost(:,6);
costc=gencost(:,7);  
StartCost=gencost(:,2);
ShutCost=gencost(:,3);
% PG0=gen(:,2);
% IS0=ones(NG,1);
% for i=1:NG
%     if PG0(i)==0
%         IS0(i)=0;
%     end
% end
PG0=zeros(NG,1);
IS0=zeros(NG,1);
Ton=3;%开关机时间可修改
Toff=2;
​
pela=zeros(NT,NT);
em=0.4;
et=2;
for i=1:NT
    pela(i,i)=-em;
    num_period=0;
    for j=i-et:i+et
        if j>0 && j<=NT && j~=i
            num_period=num_period+1;
        end
    end
    for j=i-et:i-1
        if j>0
            pela(j,i)=em/num_period;
        end
    end
    for j=i+1:i+et
        if j<=NT
            pela(j,i)=em/num_period;
        end
    end
end
price0=[18 18 18 18 18 18 21 21 23 23 23 23 23 23 23 23 21 21 21 21 21 21 18 18]';
price0=price0(1:NT);
LPDRmax=0.2;
% LPDRmax=0;
​
CRGu=15;
CRGd=8;
CRL=30;
CWc=10;
CLs=1000;
​
M_l=Fmax(:,1)+2*pi./X(:,1);
M_rho=10000;
M=10000;
​
itermax=99;
e=0.001;
UB=zeros(1,itermax);
UB(1)=999999999;
LB=zeros(1,itermax);
LB(1)=-999999999;
gap_cal=zeros(1,itermax);
PWu_return=zeros(NW,NT,itermax);
zl_return=zeros(NL,1,itermax);
​
%% 子问题对偶问题左端系数矩阵
lambda_PG=zeros(NB*NT,NG*NT);
for i=1:NT
    lambda_PG((i-1)*NB+1:i*NB,i*NG-NG+1:i*NG)=G2B;
end
lambda_PG=lambda_PG';
lambda_PW=zeros(NB*NT,NW*NT);
for i=1:NT
    lambda_PW((i-1)*NB+1:i*NB,i*NW-NW+1:i*NW)=W2B;
end
lambda_PW=lambda_PW';
lambda_Flow=zeros(NB*NT,NL*NT);
for i=1:NT
    lambda_Flow((i-1)*NB+1:i*NB,i*NL-NL+1:i*NL)=-B2B;
end
lambda_Flow=lambda_Flow';
lambda_LIDR=eye(NB*NT);
lambda_LS=eye(NB*NT);
​
mu_Flow=eye(NL*NT);
mu_Theta=zeros(NL*NT,NB*NT);
for i=1:NT
    mu_Theta((i-1)*NL+1:i*NL,(i-1)*NB+1:i*NB)=-baseMVA*B2B';
    for j=1:NL
        mu_Theta((i-1)*NL+j,(i-1)*NB+1:i*NB)=mu_Theta((i-1)*NL+j,(i-1)*NB+1:i*NB)/X(j,1);
    end
end
mu_Theta=mu_Theta';
​
nu_Flow=eye(NL*NT,NL*NT);
​
kappa_Theta=eye(NB*NT,NB*NT);
​
beta_PG=eye(NG*NT);
beta_dPu=-eye(NG*NT);
beta_dPd=eye(NG*NT);
​
delta_dPu=eye(NG*NT);
​
gamma_dPd=eye(NG*NT);
​
rho_PW=eye(NW*NT);

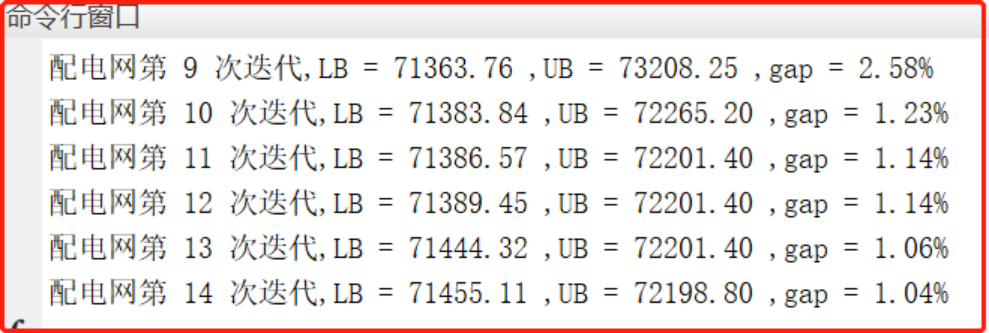
3 程序结果

4 下载链接