文章目录
- 1、前言
- 2、神经网络参数优化器
- 2.1、SGD
- 2.2、SGDM
- 2.3、Adagrad
- 2.4、RMSProp
- 2.5、Adam
- 3、实验对比不同优化器
- 4、结果对比
1、前言
- 此前,在【tensorflow框架神经网络实现鸢尾花分类】一文中使用梯度下降算法SGD,对权重 w w w和偏置 b b b进行更新,本篇将对比不同优化器的训练效果
2、神经网络参数优化器
- 待优化参数 w w w,损失函数 l o s s loss loss,学习了 l r lr lr,每次迭代一个 b a t c h batch batch, t t t表示当前 b a t c h batch batch迭代的总次数:
- 计算t时刻损失函数关于当前参数的梯度 g t = ∇ l o s s = ∂ l o s s ∂ w t g_t=\nabla loss=\frac{\partial loss}{\partial w_t} gt=∇loss=∂wt∂loss
- 计算 t t t时刻的一阶动量 m t m_t mt和二阶动量 V t V_t Vt
- 计算 t t t时刻的下降梯度: η t = l r ∗ m t V t η_t=lr*\frac{m_t}{\sqrt{V_t}} ηt=lr∗Vtmt
- w t + 1 = w t − η t = w t − l r ∗ m t V t w_{t+1}=w_t-η_t=w_t-lr*\frac{m_t}{\sqrt{V_t}} wt+1=wt−ηt=wt−lr∗Vtmt
- 一阶动量:与梯度相关的函数
- 二阶动量:与梯度平方相关的函数
2.1、SGD
- 随机梯度下降(stochastic gradient descent,SGD),无动量momentum,常用的梯度下降法。
m t = g t m_t=g_t mt=gt
V t = 1 V_t=1 Vt=1
η t = l r ∗ m t V t = l r ∗ g t η_t=lr*\frac{m_t}{\sqrt{V_t}}=lr*g_t ηt=lr∗Vtmt=lr∗gt
w t + 1 = w t − η t = w t − l r ∗ m t V t = w t − l r ∗ g t w_{t+1}=w_{t}-η_{t}=w_t-lr*\frac{m_t}{\sqrt{V_t}}=w_t-lr*g_t wt+1=wt−ηt=wt−lr∗Vtmt=wt−lr∗gt
w t + 1 = w t − l r ∗ ∂ l o s s ∂ w t w_{t+1}=w_t-lr*\frac{\partial loss}{\partial w_t} wt+1=wt−lr∗∂wt∂loss
- 代码
# sgd
w.assign_sub(lr * grads[0]) # 参数w自更新
b.assign_sub(lr * grads[1]) # 参数b自更新
2.2、SGDM
- SGDM(SGD with momentum,SGDM),在SGD的基础上增加一阶动量。
- m t − 1 m_{t-1} mt−1表示上一时刻的一阶动量,并且上一时刻的一阶动量在公式中占主导,经验值是0.9。
m t = β ∗ m t − 1 + ( 1 − β ) ∗ g t m_t=β*m_{t-1} + (1-β)*g_t mt=β∗mt−1+(1−β)∗gt
V t = 1 V_t=1 Vt=1
η t = l r ∗ m t V t = l r ∗ m t = l r ∗ ( β ∗ m t − 1 + ( 1 − β ) ∗ g t ) η_t=lr*\frac{m_t}{\sqrt{V_t}}=lr*m_t=lr*(β*m_{t-1} + (1-β)*g_t) ηt=lr∗Vtmt=lr∗mt=lr∗(β∗mt−1+(1−β)∗gt)
w t + 1 = w t − η t = w t − l r ∗ m t V t = w t − l r ∗ ( β ∗ m t − 1 + ( 1 − β ) ∗ g t ) w_{t+1}=w_{t}-η_{t}=w_t-lr*\frac{m_t}{\sqrt{V_t}}=w_t-lr*(β*m_{t-1} + (1-β)*g_t) wt+1=wt−ηt=wt−lr∗Vtmt=wt−lr∗(β∗mt−1+(1−β)∗gt)
- 代码
m_w, m_b = 0, 0
beta = 0.9
# sgd-momentun
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)
2.3、Adagrad
- Adagrad,在SGD的基础上增加二阶动量。
- 二阶动量是从开始到现在,梯度平方的累计和。
m t = g t m_t=g_t mt=gt
V t = ∑ τ = 1 t g τ 2 V_t=\sum_{τ=1}^{t}g_{τ}^{2} Vt=∑τ=1tgτ2
η t = l r ∗ m t V t = l r ∗ m t = l r ∗ g t ∑ τ = 1 t g τ 2 η_t=lr*\frac{m_t}{\sqrt{V_t}}=lr*m_t=\frac{lr*g_t}{\sqrt{\sum_{τ=1}^{t}g_{τ}^{2}}} ηt=lr∗Vtmt=lr∗mt=∑τ=1tgτ2lr∗gt
w t + 1 = w t − η t = w t − l r ∗ g t ∑ τ = 1 t g τ 2 w_{t+1}=w_{t}-η_{t}=w_t-\frac{lr*g_t}{\sqrt{\sum_{τ=1}^{t}g_{τ}^{2}}} wt+1=wt−ηt=wt−∑τ=1tgτ2lr∗gt
- 代码
v_w, v_b = 0, 0
# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
2.4、RMSProp
- RMSProp,在SGD的基础上增加二阶动量。
- 二阶动量使用指数滑动平均值计算,表征的是过去一段时间的平均值。
m t = g t m_t=g_t mt=gt
V t = β ∗ V t − 1 + ( 1 − β ) ∗ g t 2 V_t=β*V_{t-1} +(1-β)*g_{t}^{2} Vt=β∗Vt−1+(1−β)∗gt2
η t = l r ∗ m t V t = l r ∗ g t β ∗ V t − 1 + ( 1 − β ) ∗ g t 2 η_t=lr*\frac{m_t}{\sqrt{V_t}}=\frac{lr*g_t}{\sqrt{β*V_{t-1} +(1-β)*g_{t}^{2}}} ηt=lr∗Vtmt=β∗Vt−1+(1−β)∗gt2lr∗gt
w t + 1 = w t − η t = w t − l r ∗ g t β ∗ V t − 1 + ( 1 − β ) ∗ g t 2 w_{t+1}=w_{t}-η_{t}=w_t-\frac{lr*g_t}{\sqrt{β*V_{t-1} +(1-β)*g_{t}^{2}}} wt+1=wt−ηt=wt−β∗Vt−1+(1−β)∗gt2lr∗gt
- 代码
v_w, v_b = 0, 0
beta = 0.9
# rmsprop
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
2.5、Adam
- Adam,同时结合SGDM的一阶动量和RMSProp的二阶动量。
- 在一阶动量和二阶动量的基础上,加入了修正项。
m t = β 1 ∗ m t − 1 + ( 1 − β 1 ) ∗ g t m_t=β_1*m_{t-1} + (1-β_1)*g_t mt=β1∗mt−1+(1−β1)∗gt
修正一阶动量的偏差: m t ^ = m t 1 − β 1 t \hat{m_t}=\frac{m_t}{1-β_{1}^{t}} mt^=1−β1tmt
V t = β 2 ∗ V t − 1 + ( 1 − β 2 ) ∗ g t 2 V_t=β_2*V_{t-1} +(1-β_2)*g_{t}^{2} Vt=β2∗Vt−1+(1−β2)∗gt2
修正二阶动量的偏差: V t ^ = V t 1 − β 2 t \hat{V_t}=\frac{V_t}{1-β_{2}^{t}} Vt^=1−β2tVt
η t = l r ∗ m t ^ V t ^ = l r ∗ m t 1 − β 1 t V t 1 − β 2 t η_t=lr*\frac{\hat{m_t}}{\sqrt{\hat{V_t}}}=lr*\frac{\frac{m_t}{1-β_{1}^{t}}}{\frac{V_t}{1-β_{2}^{t}}} ηt=lr∗Vt^mt^=lr∗1−β2tVt1−β1tmt
w t + 1 = w t − η t = w t − l r ∗ m t 1 − β 1 t V t 1 − β 2 t w_{t+1}=w_{t}-η_{t}=w_t-lr*\frac{\frac{m_t}{1-β_{1}^{t}}}{\frac{V_t}{1-β_{2}^{t}}} wt+1=wt−ηt=wt−lr∗1−β2tVt1−β1tmt
- 代码
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0
# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))
w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
3、实验对比不同优化器
- 在此前代码中【tensorflow框架神经网络实现鸢尾花分类】替换优化器部分,加入时间模块,进行时间对比,以及训练曲线的对比。
- Adam代码示例
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time ##1##
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
##########################################################################
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0
##########################################################################
# 训练部分
now_time = time.time() ##2##
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
##########################################################################
global_step += 1
##########################################################################
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))
w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
##########################################################################
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
total_time = time.time() - now_time
print("total_time", total_time)
# 绘制测试Acc曲线和训练loss曲线
fig, ax = plt.subplots()
ax.plot(train_loss_results,'b-')
ax.set_xlabel('Epoch')
ax.set_ylabel('Loss')
ax1 = ax.twinx()
ax1.plot(test_acc,'r-')
ax1.set_ylabel('Acc')
ax1.spines['left'].set_color('blue')
ax1.spines['right'].set_color('red')
ax.set_title('SGD', fontsize=12)
4、结果对比
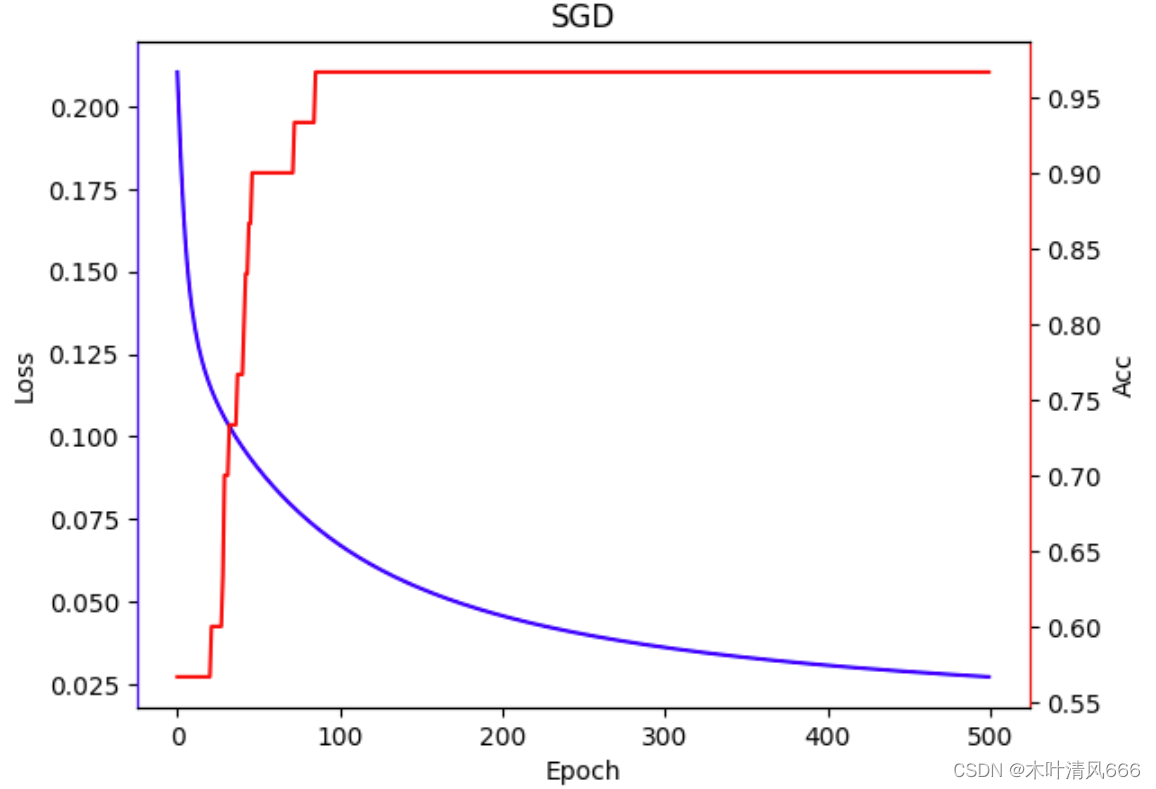
| 优化器 | 训练用时 | 结果可视化 |
|---|---|---|
| SGD | 8.742414951324463 | 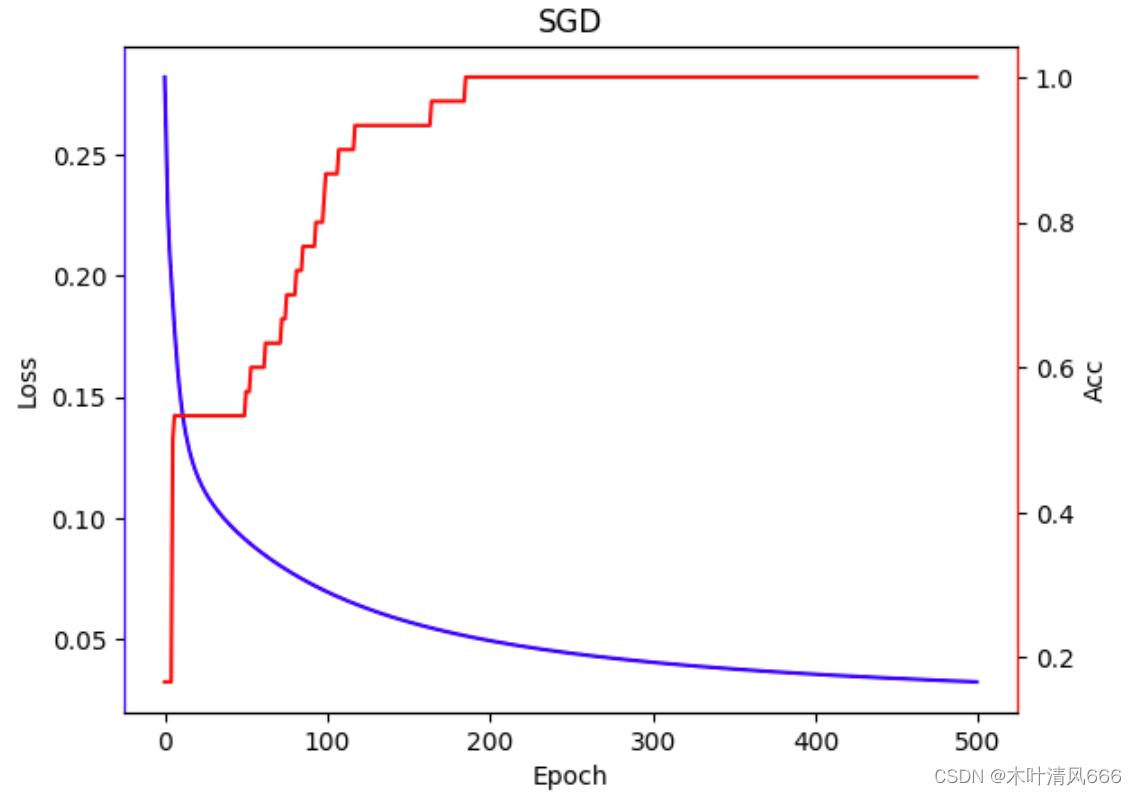 |
| SGDM | 8.880060911178589 | 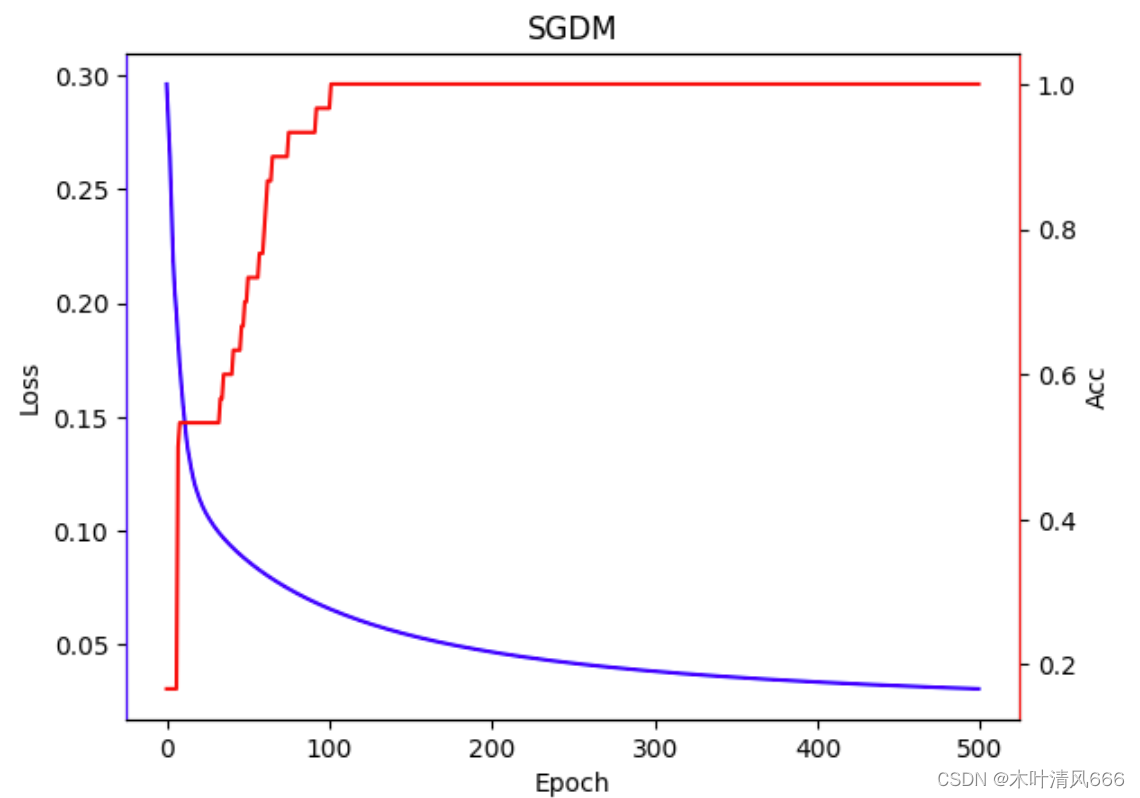 |
| Adagrad | 8.902021646499634 | 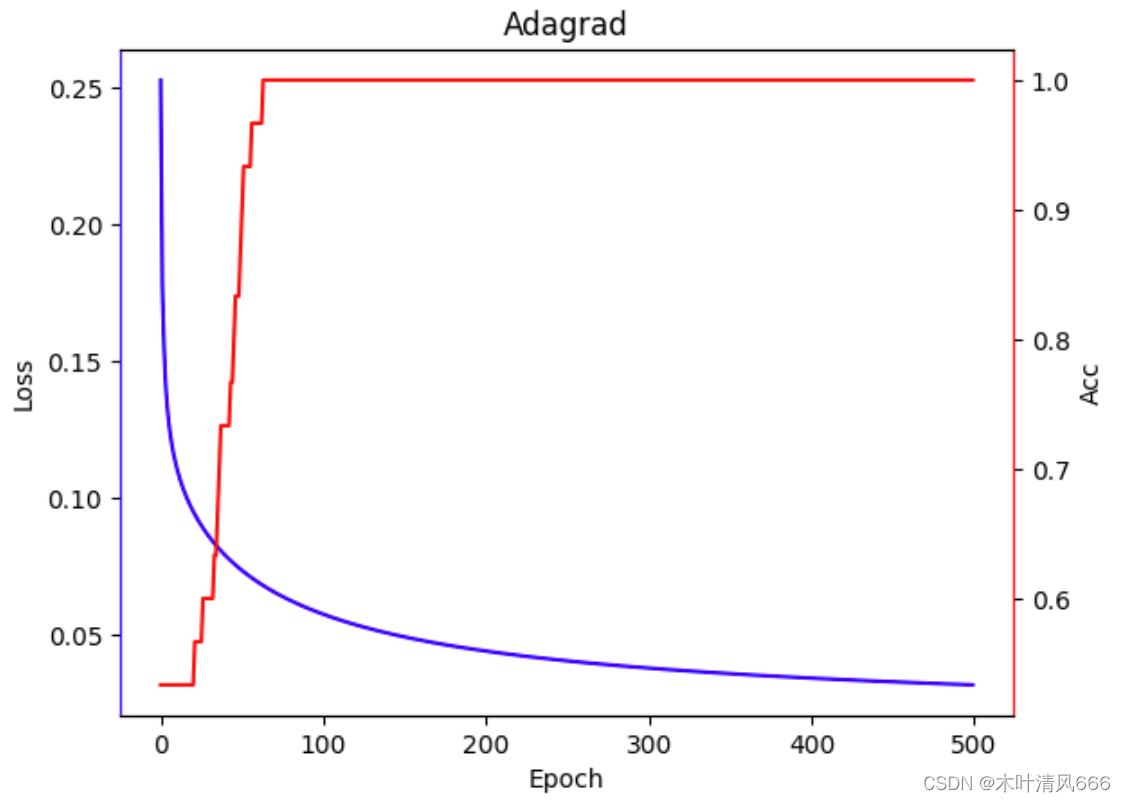 |
| RMSProp | 9.599585771560669 | 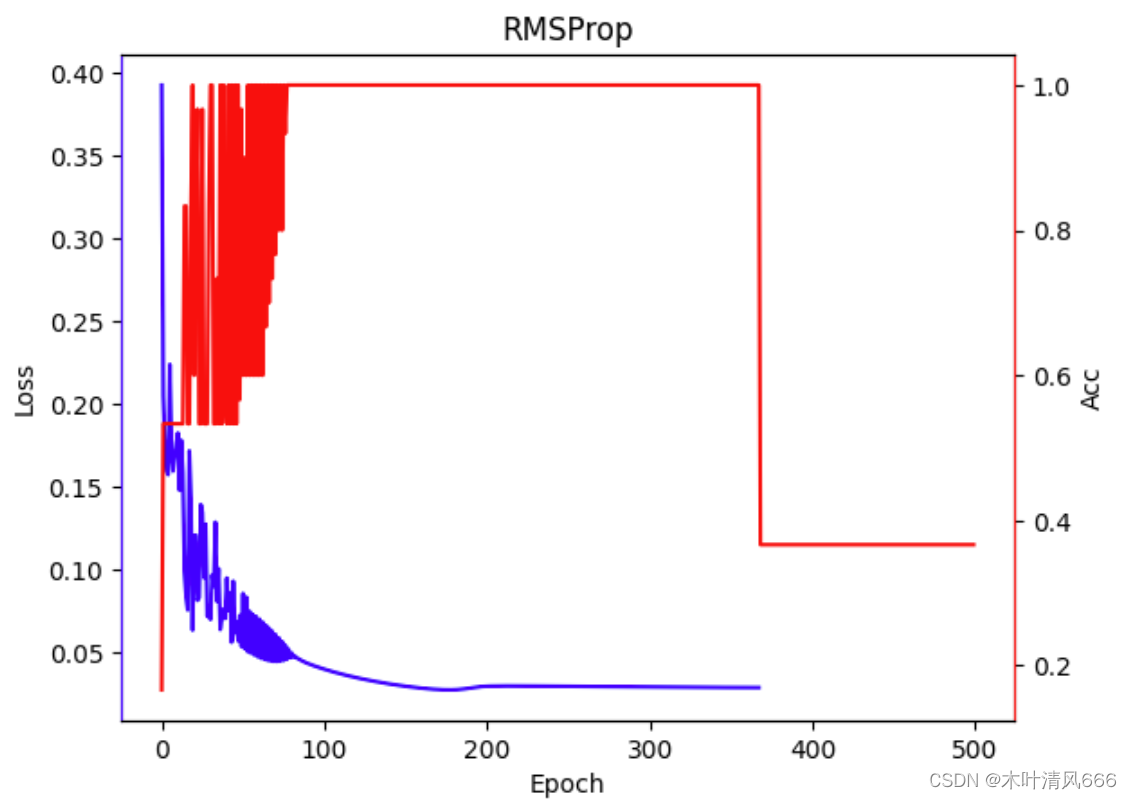 |
| Adam | 10.520380973815918 | 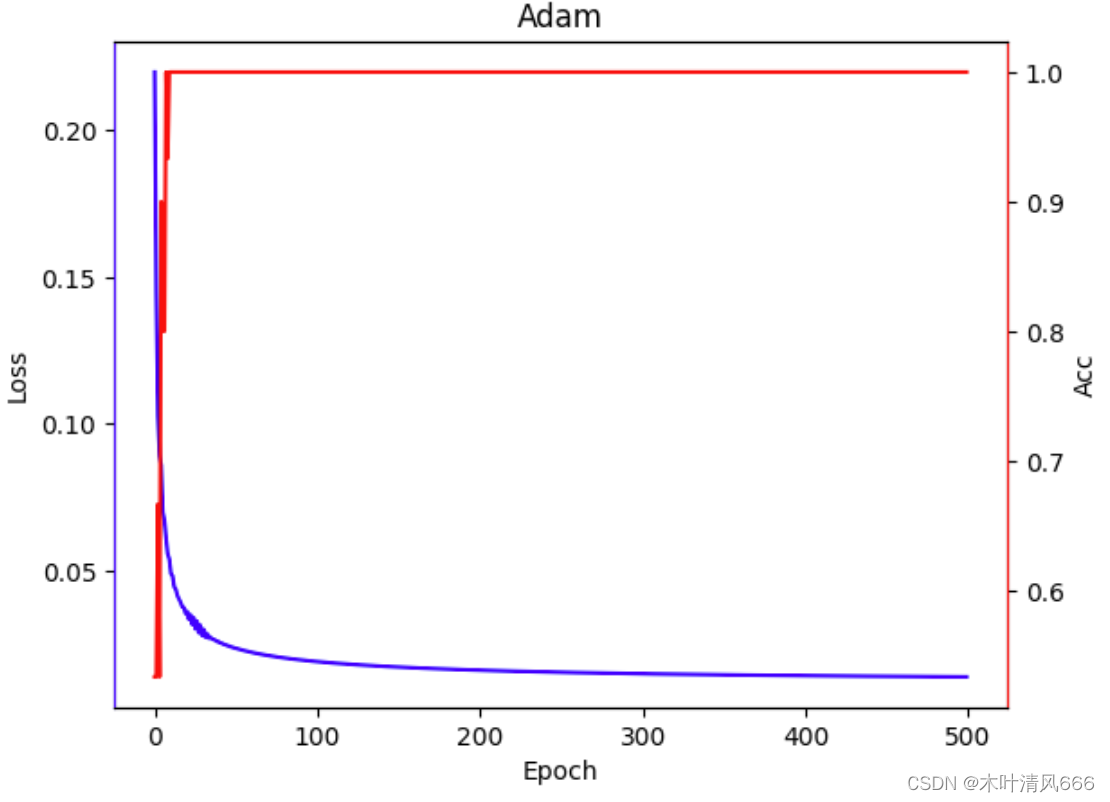 |
学习视频参考:https://www.bilibili.com/video/BV1B7411L7Qt/