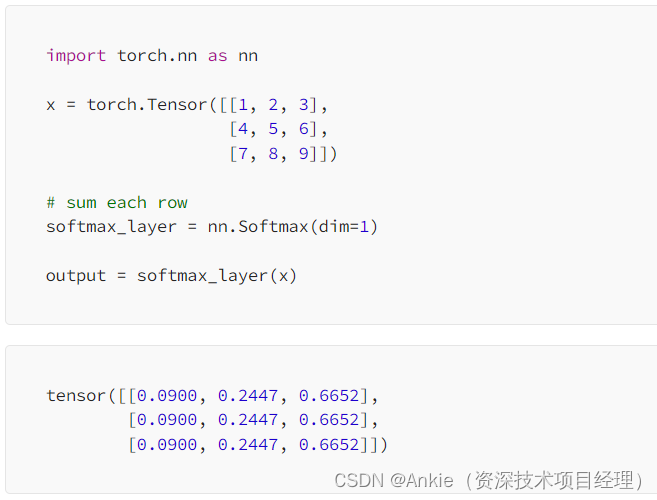
蓝桥杯练习笔记（十六）

一、

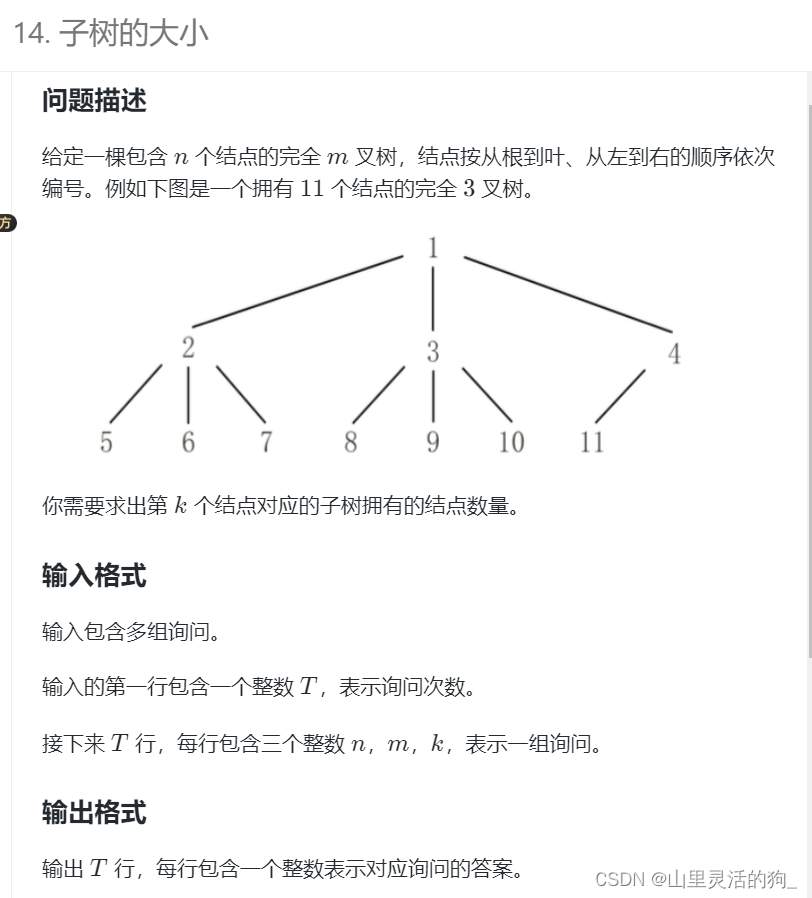
• 输入示例：

3
1 2 1
11 3 4
74 5 3

这是用到了m叉树的结论：对于某个m叉树的一个节点n，假如其有完整子树，则其左子节点l为l=(n-1)m+2，右子节点r为r=mn+1。基于此我们可以快速判断这个数在某些节点处的具体情况。比如是否是满叶子等等。

• 蓝桥官网题解：

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
int main()
{
  int t;
  scanf("%d",&t);
  while(t--)
  {
      ll n,m,k;
      scanf("%lld%lld%lld",&n,&m,&k);
      ll l=k,r=k;//初始化左右子节点
      ll res=1,ans=1;//初始化每一行的节点数和总节点数
      while(r*m+1<=n)//当右子节点编号小于n时，说明该行它的子节点全部存在
      {
         res*=m;//全部存在时，直接*m
         l=(l-1)*m+2; //左子节点的左子节点
         r=r*m+1; //右子节点的右子节点
       //    他们之间就第k的节点的子节点
         ans+=res; //当全部存在时，加上该层所有子节点个数
      }
//出来之后，说明当前这一行，以第k个节点为根节点的子节点不完全存在，甚至可能没有
      l=(l-1)*m+2;//由于循环打断，右边界无所谓，因为已经出界，左边界却没有更新，所以需要更
      ans+=max(0ll,n-l+1);//比较需要时同等数据类型，因为有可能是负数，最后一行一个子节点无
      cout<<ans<<endl;
  }
  return 0;
}