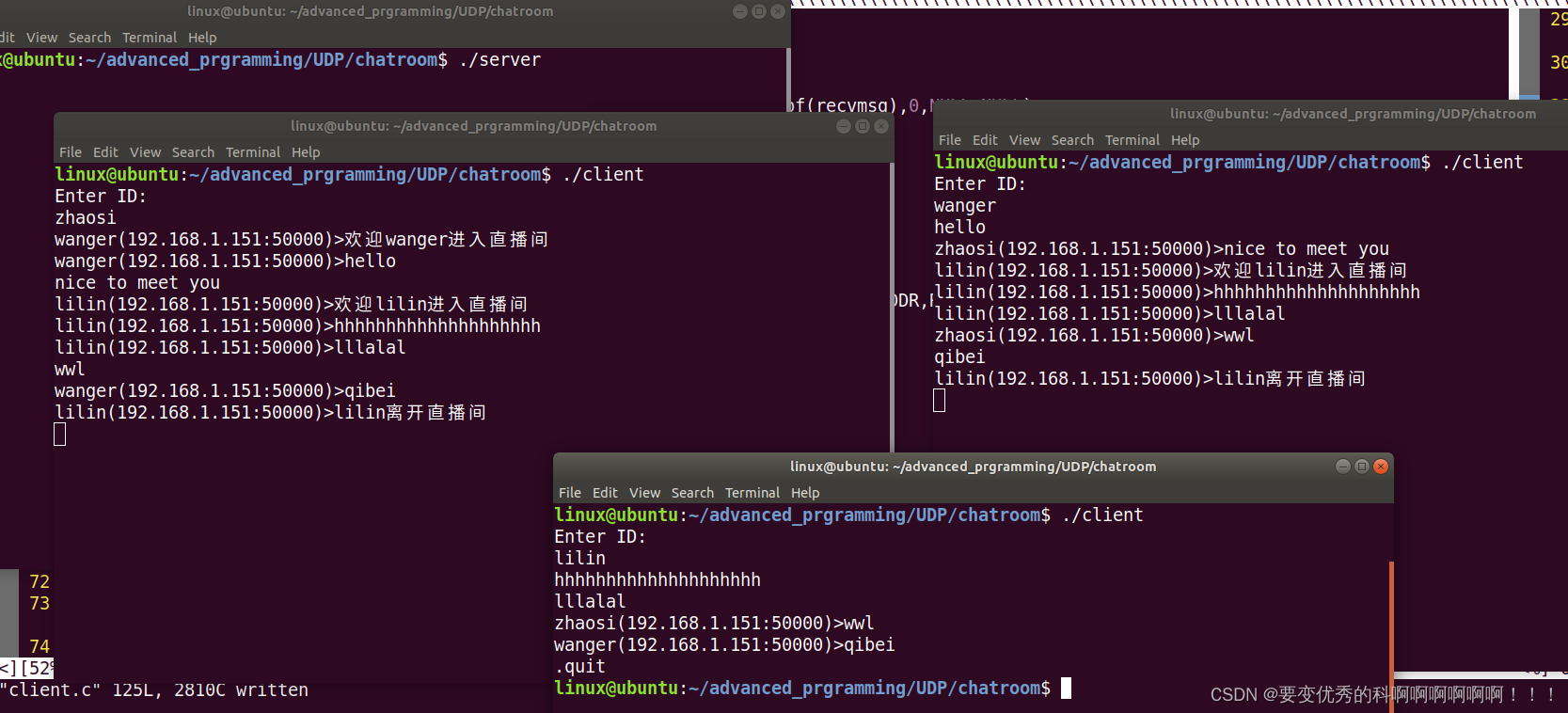
解题思路：

经典dfs题目，需要重点掌握。

养成好习惯，静态方法都要用到的变量提前想到定义为静态常量。

import java.util.Scanner;

public class Main {
    //注意加static，经常忘记导致编译错误
    static int N, M, x1, x2, y1, y2, min = Integer.MAX_VALUE;
    static int[][] a, v;

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        N = scan.nextInt();
        M = scan.nextInt();
        
        // 初始化网格，注意题目条件，出发点和终点的坐标都是从1开始，所以我们的下标不能像往常一样从0开始
        a = new int[N + 1][M + 1];
        //初始化记录最少步数的访问数组
        v = new int[N + 1][M + 1];

        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= M; j++) {
                a[i][j] = scan.nextInt();
                //赋最大值，代表没有被访问过
                v[i][j] = Integer.MAX_VALUE;
            }
        }

        x1 = scan.nextInt();
        y1 = scan.nextInt();
        x2 = scan.nextInt();
        y2 = scan.nextInt();
        
        dfs(0, x1, y1);
        
        // 如果找不到路径，则输出-1，否则输出最短路径长度
        if (min == Integer.MAX_VALUE) {
            min = -1;
        }
        System.out.println(min);
    }

    public static void dfs(int step, int x, int y) {
        v[x][y] = step;
        if (x == x2 && y == y2) {
            min = Math.min(min, step);
            return;
        }
        
        // 方向数组
        int[] dx = { 1, -1, 0, 0 };
        int[] dy = { 0, 0, 1, -1 };
        
        // 尝试向四个方向搜索
        for (int i = 0; i < 4; i++) {
            int xx = x + dx[i];
            int yy = y + dy[i];
            //注意v[x][y] + 1 < v[xx][yy]，我们继续dfs的前提是v[xx][yy]没有被访问，
            //或当前路径长度加1到达v[xx][yy]后比v[xx][yy]本身的路径更短
            if (xx > 0 && yy > 0 && xx <= N && yy <= M && v[x][y] + 1 < v[xx][yy] && a[xx][yy] == 1) {
                dfs(step + 1, xx, yy);
            }
        }
    }
}