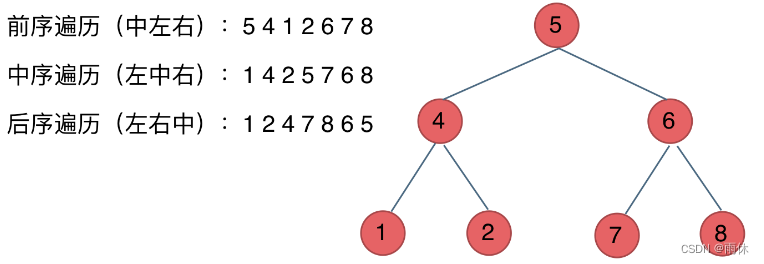
01.在有n个叶结点的哈夫曼树中,非叶结点的总数是( A ).
A. n-1 B. n C. 2n-1 D.2n
解析:哈夫曼树中只有度为0和2的结点,在非空二叉树中,有n0=n2+1,所以n2=n-1
02.给定整数集合{3,5,6,9,12},与之对应的哈夫曼树是( C ).
解析:3和5构造一棵子树,根权值为8,然后该子树与6构成一棵新子树,根权值为14,9与12构造一棵子树,最后两棵子树共同构造为一棵哈夫曼树
03.下列编码中,( B )不是前缀码。
A.{00,01,10,11}
B.{0,1, 00,11}
C. {0,10,110,111}
D. {10,110,1110,1111}
解析:若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码,选项B中,0是00的前缀,1是11的前缀
04.设哈夫曼编码的长度不超过4,若已对两个字符编码为1和01,则还最多可对(C )个字符编码。
A.2 B.3 C.4 D.5
解析:只能为0010、0000、0001、0011这四种
05.一棵哈夫曼树共有215个结点,对其进行哈夫曼编码,共能得到( B )个不同的码字。
A.107 B.108 C.214 D.215
解析:叶结点数=(215+1)/2=108
06.设某哈夫曼树有5个叶结点,则该哈夫曼树的高度最高可以是( C ).
A.3 B.4 C. 5 D.6
解析:每个初始结点最终都成为叶结点,则5个初始结点可构建4个双分支结点,如下图所示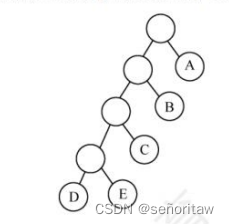
07.以下对于哈夫曼树的说法中,错误的是(D)
A.对应一组权值构造出来的哈夫曼树一般不是唯一的
B.哈夫曼树具有最小的带权路径长度
C.哈夫曼树中没有度为1的结点
D.哈夫曼树中除了度为1的结点,还有度为2的结点和叶结点
解析:哈夫曼树通常指的是带权路径长度达到最小的扩充二叉树,在构造过程中每次选根权最小的两棵树,一棵作为左子树一棵作为右子树生成新的二叉树,新的二叉树根的权值为两棵子树根结点权值的和,至于谁做左子树谁做右子树没有限制,所以构造的哈夫曼树不是唯一的
哈夫曼树只有度为0和2的结点,度为0的结点是外结点,带有权值,没有度为1的结点
08.下列关于哈夫曼树的说法中,错误的是(C).
I.哈夫曼树的结点总数不能是偶数
Ⅱ.哈夫曼树中度为1的结点数等于度为2和0的结点数之差
Ⅲ.哈夫曼树的带权路径长度等于其所有分支结点的权值之和
A.仅Ⅲ B.I和Ⅱ C.仅Ⅱ D. I、Ⅱ和Ⅲ
解析:n个初始结点构造的哈夫曼树工新建n-1个双分支结点,因此哈夫曼树的结点总数是个奇数
哈夫曼树中没有度为1的结点,哈夫曼树的带权路径长度有两个方法:①所有叶结点的带权路径长度之和,②所有分支结点的权值之和
09.若度为m的哈夫曼树中,叶结点个数为n,则非叶结点的个数为( C ).
A. n-1 B. ⌊n/m⌋-1 C.⌈(n-1)/(m-1)⌉ D.⌈n/(m-1)⌉ -1
10.并查集的结构是一种(B ).
A.二叉链表存储的二叉树 B.双亲表示法存储的树
C.顺序存储的二叉树 D.孩子表示法存储的树
解析:并查集的存储结构是用双亲表示法存储的树,主要是为了方便并和查两个操作
11.并查集中最核心的两个操作是:①查找,查找两个元素是否属于同一个集合;②合并,若两个元素不属于同一个集合,且所在的两个集合互不相交,则合并这两个集合。假设初始长度为10 (0~9)的并查集,按1-2、3-4、5-6、7-8、8-9、1-8、0-5、1-9的顺序进行查找和合并操作,最终并查集共有(C )个集合。
A. 1 B.2 C.3 D.4
解析:查1和2 ,没在一个集合就合并,之后3和4合并,7和8合并,8和9合并,1和8合并,0和5合并,1和9本来就在一个集合了就不需要合并了,最终集合如下所示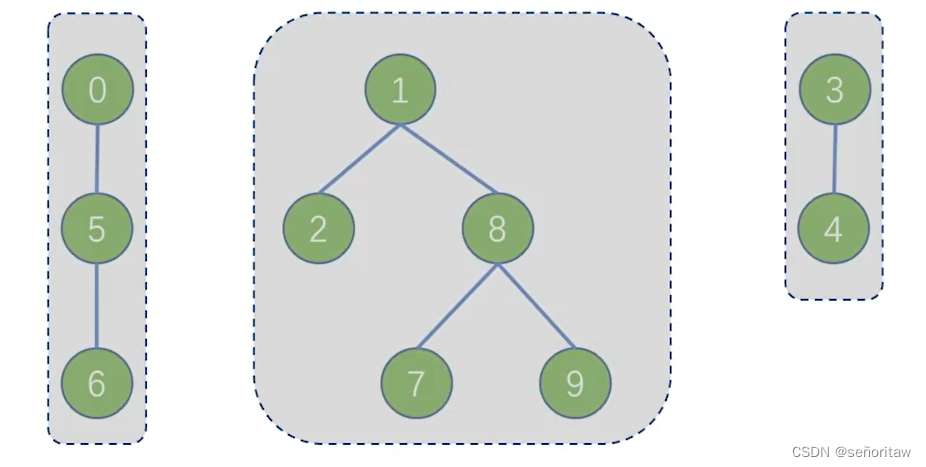
12.下列关于并查集的说法中,正确的是( D )(注,本题涉及图的考点)。
A.并查集不能检测图中是否存在环路的问题
B.通过路径优化后的并查集在最坏情况下的高度仍是O(n)
C. Find操作返回集合中元素个数的相反数,它用来作为某个集合的标志
D.并查集基于树的双亲表示法
解析:依次探测图的各条边,用并查集检查该边依附的两个顶点是否已属于同一集合(两个顶点的根结点是否相同)。若是,则说明图中存在环路,A错误。经过路径优化后,并查集在最坏情况下的高度远小于O(n),B错误。Find操作总返回当前根结点作为集合的标志,C错误。
13.下列关于并查集的叙述中,(D)是错误的(注,本题涉及图的考点)。
A.并查集是用双亲表示法存储的树
B.并查集可用于实现克鲁斯卡尔算法
C.并查集可用于判断无向图的连通性
D.在长度为n的并查集中进行查找操作的时间复杂度为O(logn)
解析:未做路径优化的并查集在最坏情况下的高度为n,此时查找操作的时间复杂度为O(n)
14.【2010统考真题】n (n≥2)个权值均不相同的字符构成哈夫曼树,关于该树的叙述中,错误的是(A )。
A.该树一定是一棵完全二叉树
B.树中一定没有度为1的结点
C.树中两个权值最小的结点一定是兄弟结点
D.树中任意一个非叶结点的权值一定不小于下一层任意一个结点的权值
解析:哈夫曼树为带权路径长度最小的二叉树,不一定是完全二叉树
15.【2014统考真题】5个字符有如下4种编码方案,不是前缀编码的是(D).
A. 01,0000,0001,001,1 B. 011,000,001,010,1
C. 000,001,010,011,100 D.0,100,110,1110,1100
解析:D中110是1100的前缀,违反了前缀编码的规则
16.【2015统考真题】下列选项给出的是从根分别到达两个叶结点路径上的权值序列,能属
于同一棵哈夫曼树的是(D).
A.24,10,5和24,10,7 B. 24,10,5和24,12,7
C. 24,10,10和24,14,11 D. 24,10,5和24,14,6
解析:画图,左右孩子权值之和为父结点权值,如选项A,24为共同结点,两个10分别属于两棵不同的子树,但10+10≠24,所以不可能在同一棵哈夫曼树上,BC也如此
17.【2017统考真题】已知字符集{a, b, c, d, e, f,g, h},若各字符的哈夫曼编码依次是0100,10,0000,0101,001,011,11, 0001,则编码序列0100 011 001 001 011 11 0101的译码结果是(D)
A. a c g a b f h B. a d b a g b b C. a f b e a g d D. a f e e f g d
18.【2018统考真题】已知字符集{a, b, c, d, e, f},若各字符出现的次数分别为6,3,8,2,10,4,
则对应字符集中各字符的哈夫曼编码可能是(A).
A. 00,1011,01,1010,11,100
B. 00,100,110,000,0010,01
C. 10,1011,11,0011, 00,010
D. 0011,10,11,0010,01, 000
解析:寻找最小的两个值画出对应的哈夫曼树,由图可知,ace的编码长度应该相同,a和c的第一个编码应该相同,且与e的第一个编码不同,b和d的前三个编码应该相同,可得出A正确
另解:一般规定对于哈夫曼树左0右1,在不限制左0右1 的情况下对答案一个一个进行匹配
19.【2019统考真题】对n个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有115个结点,则n的值是(C)
A. 56 B. 57 C. 58 D.60
解析:n个符号构成哈夫曼树的过程中共新建了n-1个结点(双分支结点),因此哈夫曼树的总结点数位2n-1=115,n的值为58
N0=N2+1,N0+N2=115,N0=115+1/2
20.【2021统考真题】若某二叉树有5个叶结点,其权值分别为10,12,16,21,30,则其最小的带权路径长度(WPL)是( B ).
A. 89 B.200 C.208 D.289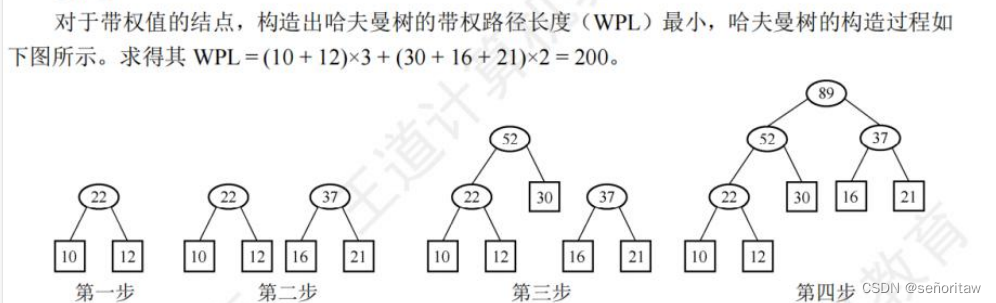

五个叶结点需要合并4个双分支结点,所以一共4个非叶结点相加
21.【2022统考真题】对任意给定的含n (n>2)个字符的有限集S,用二叉树表示S的哈夫曼编码集和定长编码集,分别得到二叉树T1和T2。下列叙述中,正确的是(D)。
A.T与T2的结点数相同
B.T的高度大于T,的高度
C.出现频次不同的字符在T1中处于不同的层
D.出现频次不同的字符在T2中处于相同的层
解析:定长编码集的定义:出现频次相同的不同的字符都处在同一层,所有字符都在同一层,所有字符的长度都是一样的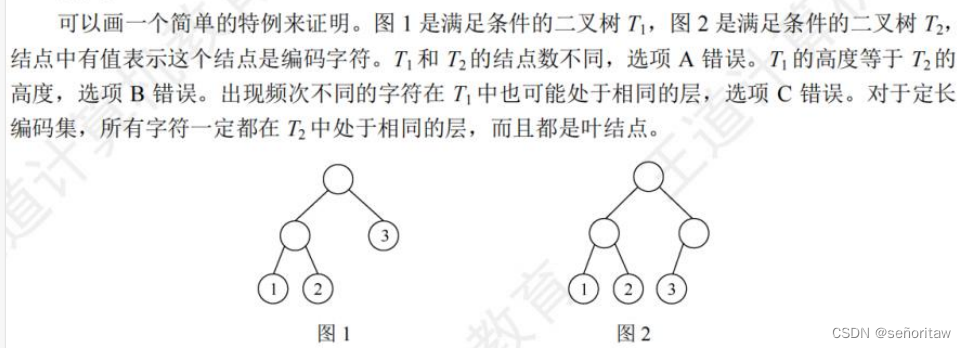
22.【2023统考真题】在由6个字符组成的字符集S中,各字符出现的频次分别为3,4,5,6,8,10,为S构造的哈夫曼编码的加权平均长度为(B).
A.2.4 B.2.5 C.2.67 D.2.75