目录
- 一、二叉排序树的定义
- 二、二叉排序树的插入和构造
- 三、二叉排序树的查找
- 四、二叉排序树的平均查找长度
- 五、二叉排序树的删除
- 六、二叉排序树和二分查找对比
二叉排序树的查找过程与折半查找(二分查找)相似,即折半查找的判定树就是一棵二叉排序树。
一、二叉排序树的定义
二叉排序树也称为二叉查找树,其中,各结点值的关系是:左子树<根结点<右子树,若对该树进行中序遍历,可得到一个递增的序列。
二、二叉排序树的插入和构造
对一棵空二叉排序树进行插入,则直接将结点插入;遵循二叉排序树各结点值的关系,若插入的结点小于根结点的值,则插入到左子树,否则插入到右子树。
例如,对于查找的关键字序列{53,17,12,66,58,70,87,25,56,60}构造二叉排序树。
1、从空树开始,依次插入元素,首先插入53,如下:

2、插入元素17,由于17<53,所以放在53的左子树:
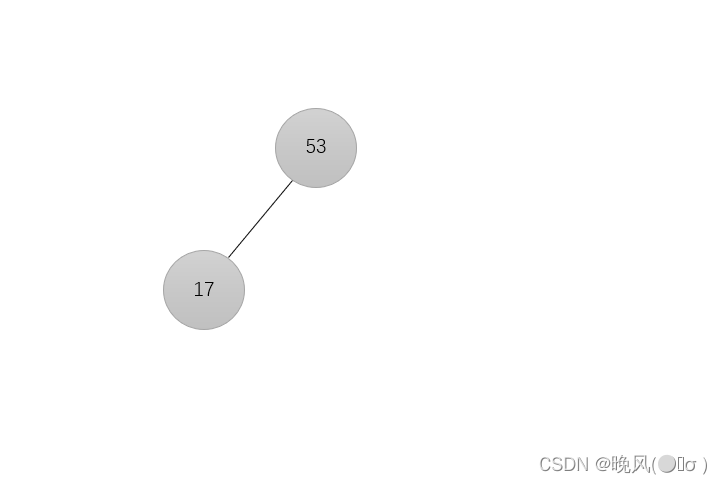
3、插入元素12,由于12<17,放在17的左子树:
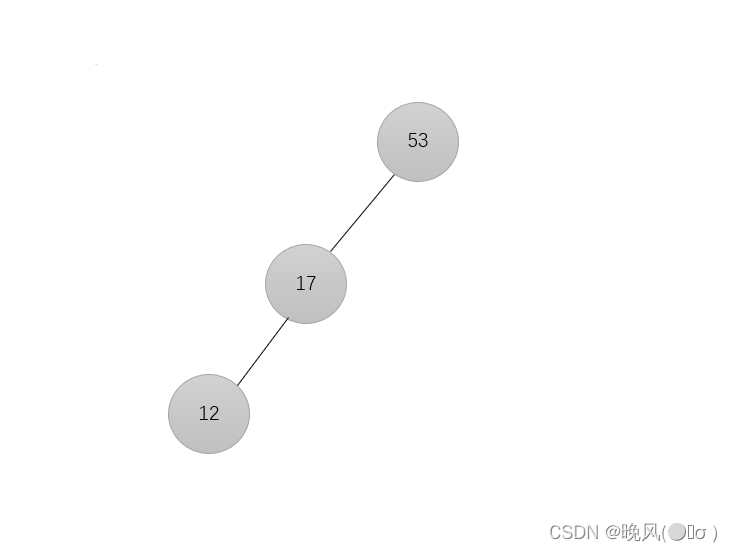
4、插入元素66,由于66>53,放在53的右子树:
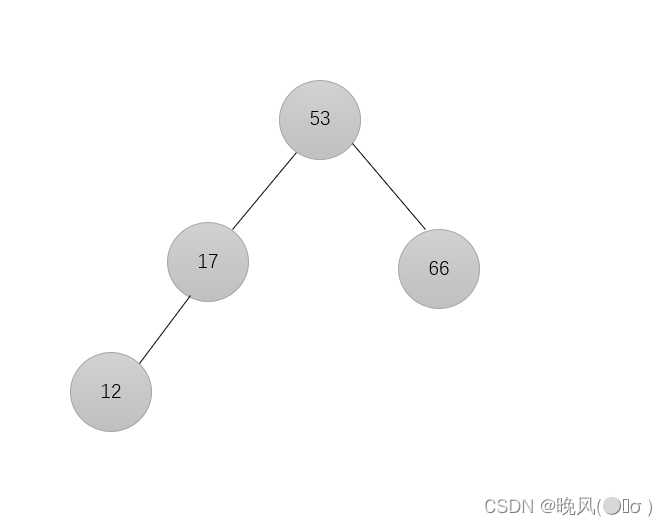
5、插入元素58,由于58<66,放在66的左子树:
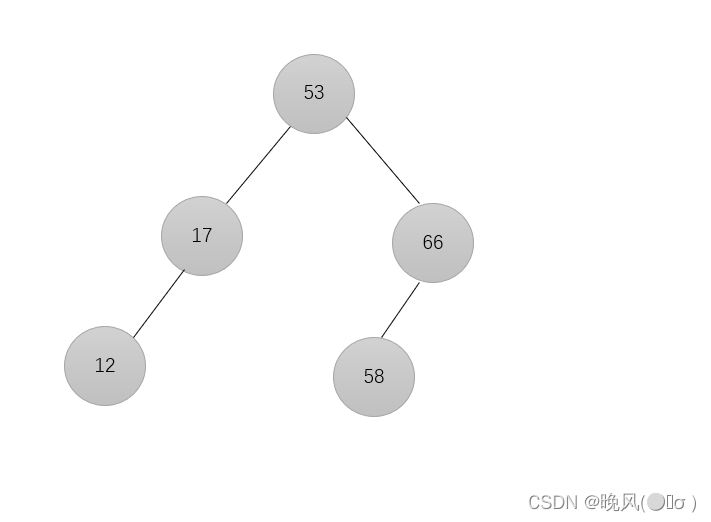
6、插入元素70,由于70>66,放在66的右子树:
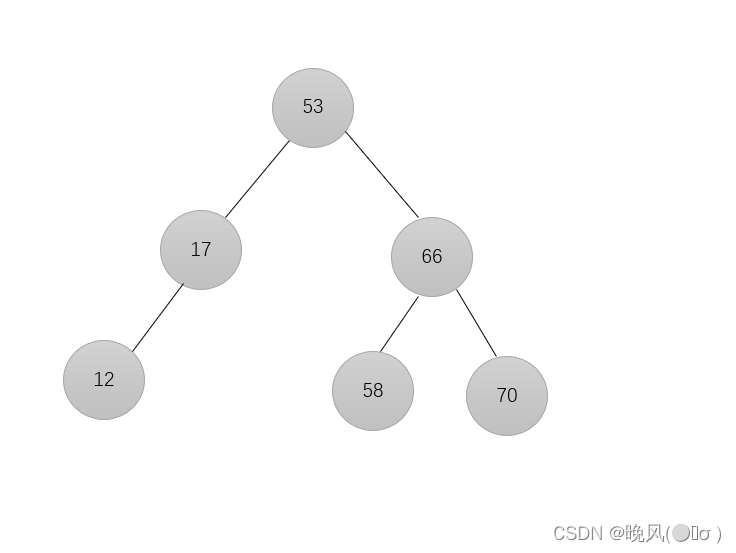
7、插入元素87,由于87>70,放在70的右子树:
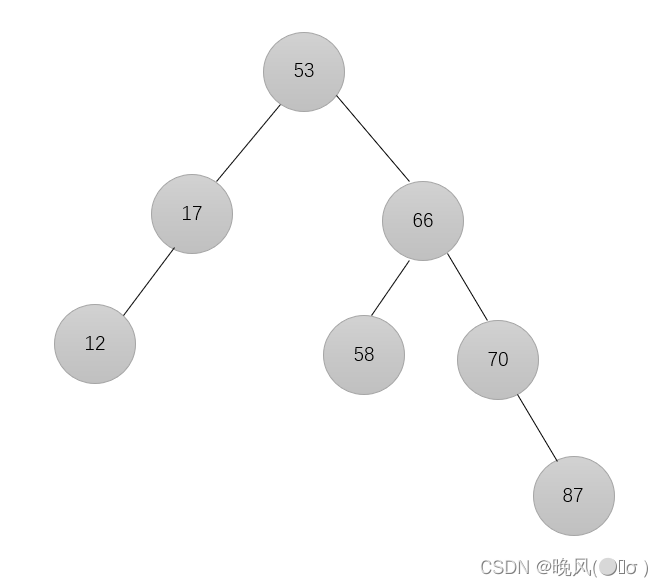
8、插入元素25,由于25>17,放在17的右子树:
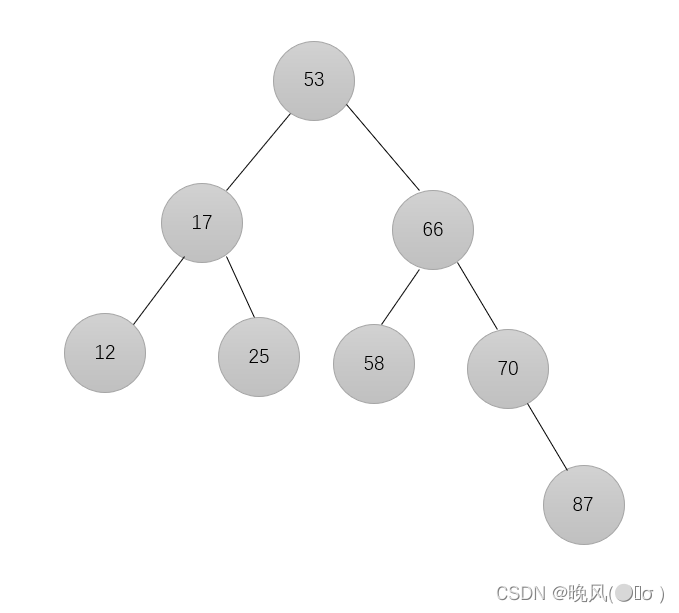
9、插入元素56,由于56<58,放在58的左子树:
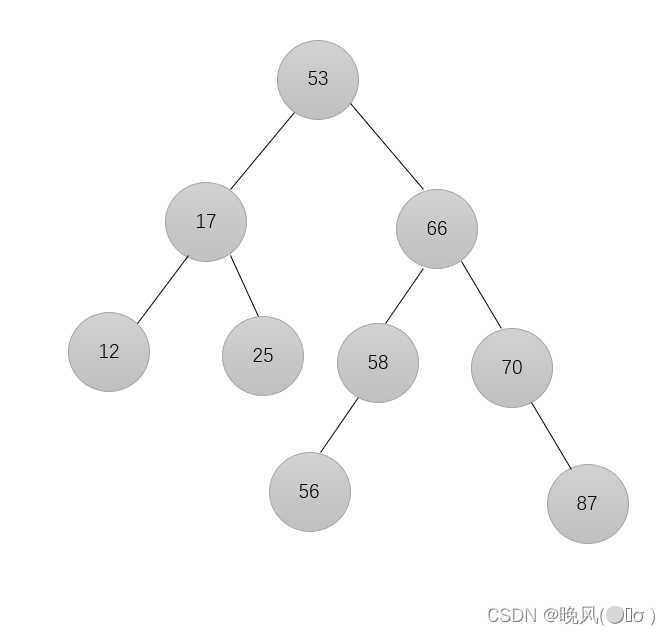
10、插入元素60,由于60>58,放在58的右子树:
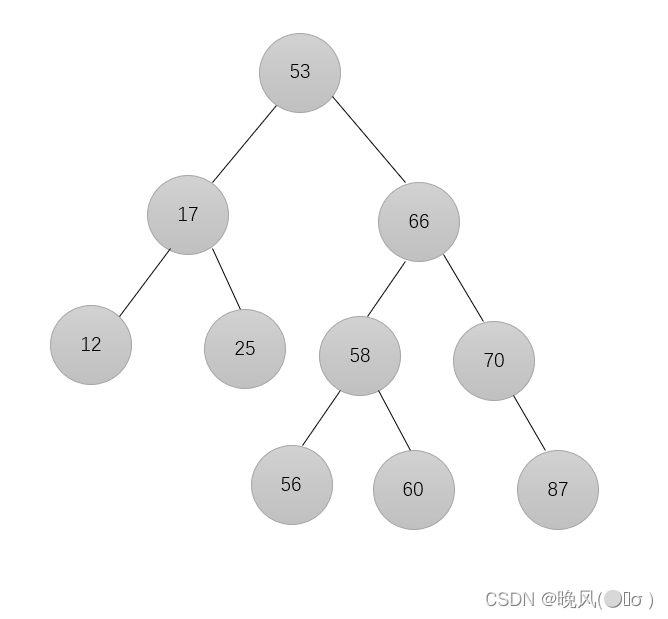
可以看出,将这棵树进行中序遍历,得到的中序遍历序列为12、17、25、53、56、58、60、66、70、87,它是一个递增序列。
三、二叉排序树的查找
二叉排序树的查找是由根结点开始,然后沿着二叉树的分支依次向下查找,若要查找的元素与当前根结点相等,则查找成功;若小于根结点,则在当前根结点的左子树上继续查找,若大于,则在当前根结点的右子树上继续查找,依次递归。
- 二叉排序树的查找效率取决于树的高度,这里给出平衡二叉树的定义(若二叉排序树的左、右子树的高度之差的绝对值不超过1,则称为平衡二叉树),其平均查找长度为O(log2n);而若二叉排序树只是一个单支树(左或右单支树),则其平均查找长度为O(n)。
四、二叉排序树的平均查找长度
- 在等概率下,二叉排序树查找成功的平均查找长度等于每层层数乘以每层结点个数之和除以二叉排序树的结点总个数。
例如,下面这个二叉排序树,在等概率下计算其查找成功的平均查找长度:

A
S
L
成功
=
(
1
×
1
+
2
×
2
+
3
×
4
+
4
×
3
)
10
=
29
10
ASL_{成功}=\frac{(1\times1+2\times2+3\times4+4\times3 )}{10} =\frac{29}{10}
ASL成功=10(1×1+2×2+3×4+4×3)=1029
五、二叉排序树的删除
在二叉排序树中删除一个结点,不能直接删除,要确保删除后的二叉排序树的性质不变,删除结点分为以下三种情况:
1、删除叶子结点
- 若删除的结点是二叉排序树的叶子结点,则可以直接删除,删除后并不影响二叉排序树的性质。
例如,删除下列二叉排序树中的87结点:
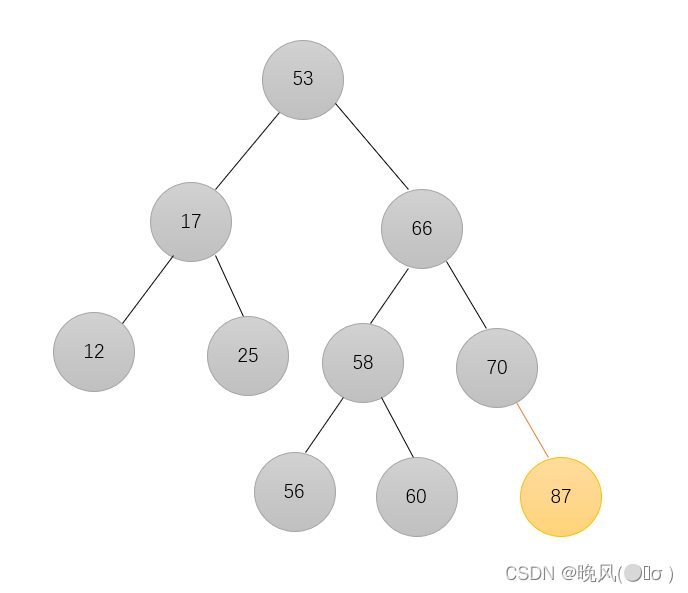
直接删除:
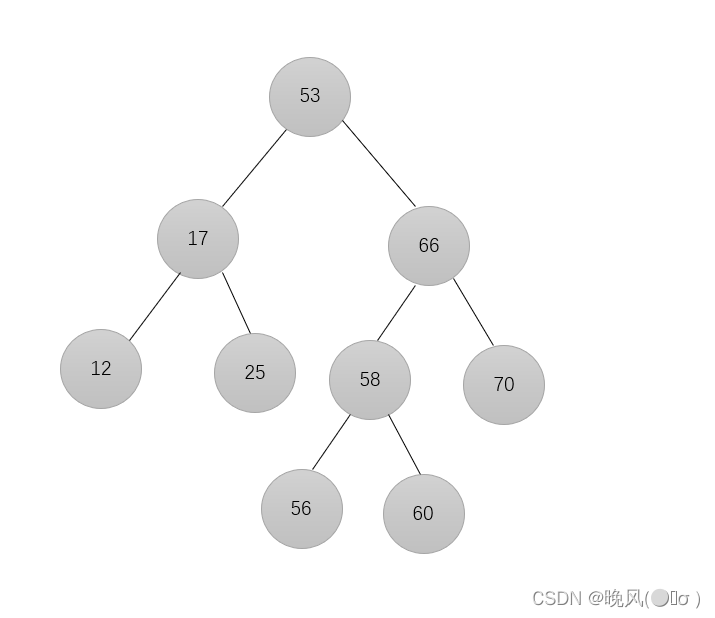
2、删除结点只存在左孩子或右孩子
- 若删除的结点存在左孩子或右孩子,则让该结点的子树成为其父结点的子结点。
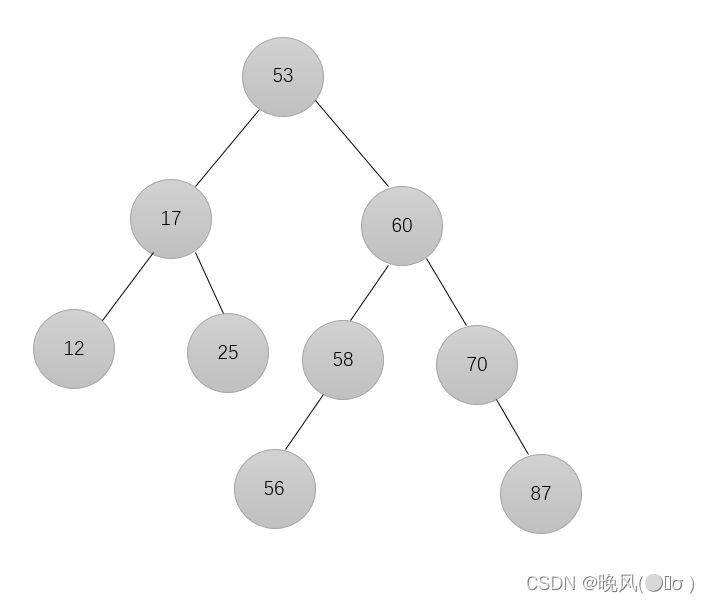
例如,删除下列二叉排序树中的70结点:
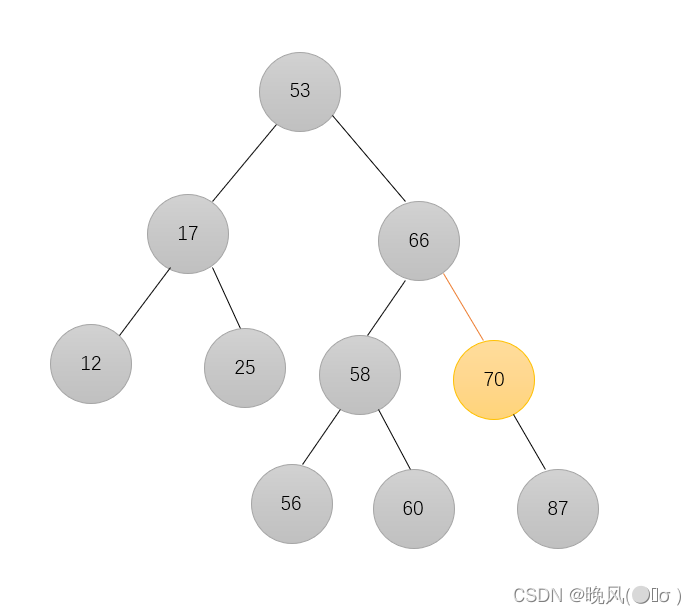
删除后,用该结点的子树(左/右孩子),即87代替它成为删除结点的父节点的子结点:
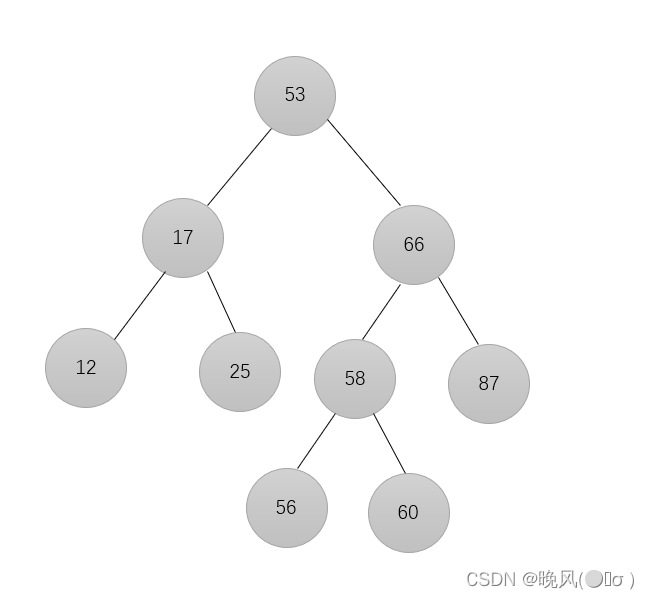
3、删除结点存在左孩子和右孩子
- 若删除结点存在左孩子和右孩子,则令该结点的前驱/后继代替它(用中序遍历序列中其前驱/后继代替),调整后的树仍是二叉排序树。
例如,删除下列二叉排序树中的66结点:
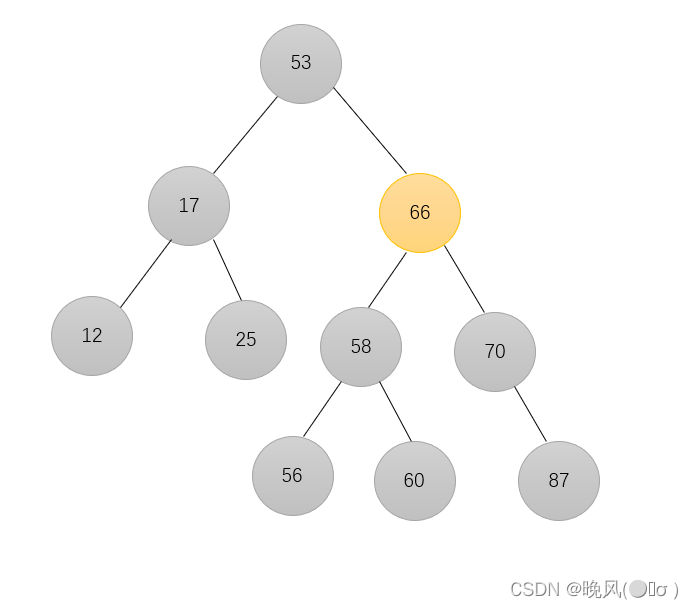
由于66结点左孩子和右孩子都存在,所以根据其中序遍历序列{12,17,25,53,56,58,60,66,70,87},选择遍历序列中66的第一个子女代替,即70代替:
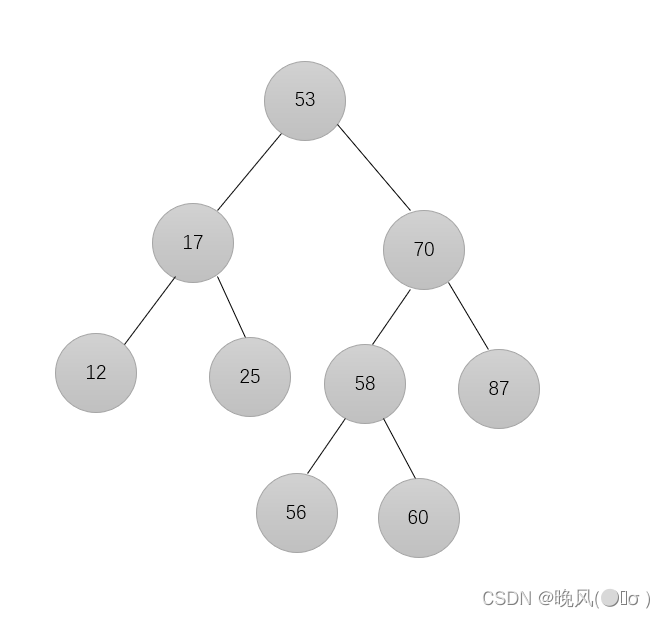
或者也可以用遍历序列中66的前驱结点60代替:
六、二叉排序树和二分查找对比
相同的关键字根据插入顺序的不同可以形成不同的二叉排序树,而二分查找的判定树是唯一的,二叉排序树中插入和删除结点操作只需修改指针,平均时间复杂度为O(log2n),而二分查找中,由于表中的元素顺序是有序的,所以插入和删除结点操作的时间复杂度为O(n)。
当有序表是静态查找表时,采用顺序表作为存储结构较合适,且采用二分查找;而若有序表是动态查找表时,采用二叉排序树作为其存储结构。