第二章.线性回归以及非线性回归

2.1 一元线性回归

1.概念：

1).自变量：

被用来进行预测的变量，相当于输入

2).因变量：

被预测的变量，相当于输出

3).回归分析：

用来建立方程模拟两个或者多个变量之间如何关联，两个以上的自变量，则称作多元回归分析。

2.一元线性回归方程：

1).ℎ𝜃𝑥 =β1𝑥+β0

参数说明：
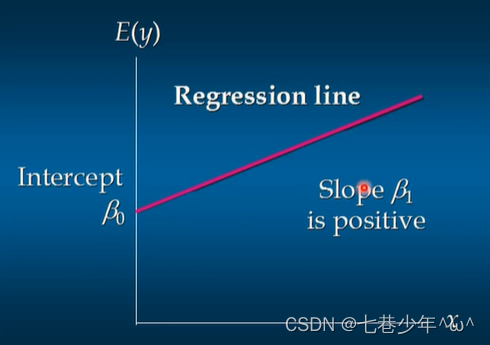
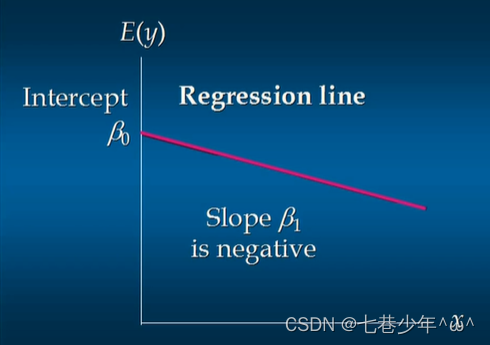
β0：回归线的截距
β1：回归线的斜率

注意：β1和β0也可以使用其他标识符代替，后续会使用θ0替代β0，θ1替代β1

2).正相关

3).负相关

4).不相关

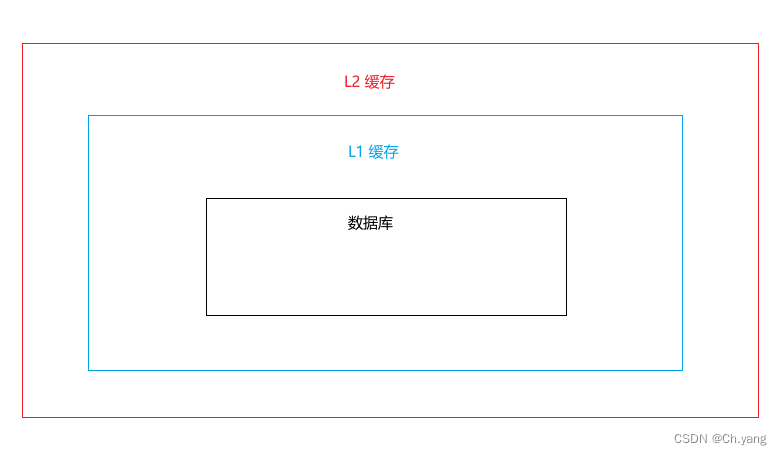
2.2 代价函数 (Cost Function)

1.概念：

1).代价函数：

也称为损失函数(Loss Function)

2).代价函数使用的算法：

最小二乘法

2.代价函数方程：

1).真实值y,预测值h0(𝑥),则误差平方为(y-h0(𝑥))^2

• 注意 :不可以用绝对值，不利于后续的计算

2).代价函数：

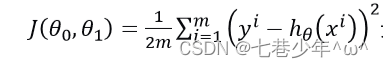
• 参数说明：
  i：样本点
  m：样本总数
  
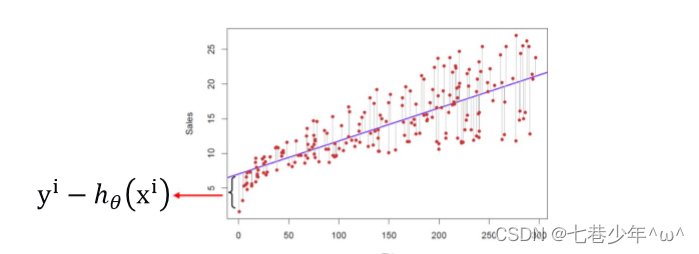
  注意：方程中的1/2参数可有可无，存在的意义是：形式比较好看，函数在对x求导的时候，^2会被提到函数前面，正好与1/2消掉

3).找到合适的参数，使得误差平方和最小

4).总结：

·公式：

·图像：

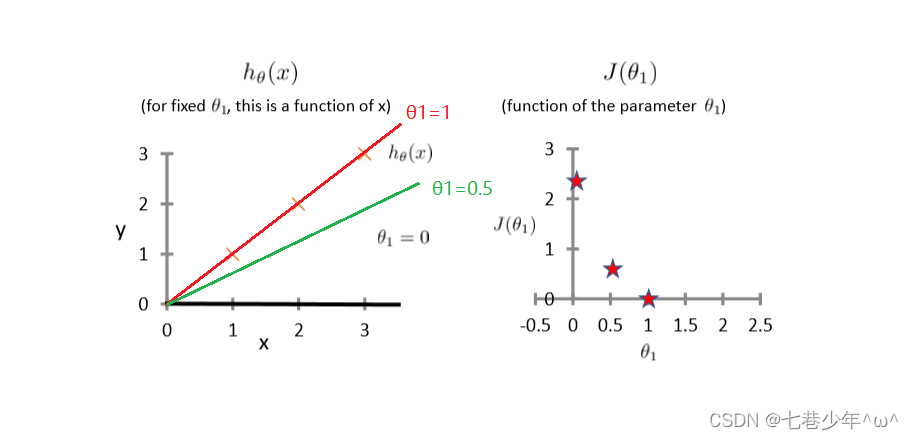
以θ1=0.5为例通过误差平方和公式画曲线：
·𝑥=1时，h0(𝑥)=0.5,平方为0.25；
·𝑥=2时，h0(𝑥)=1,平方为1；
·𝑥=3时，h0(𝑥)=1.5,平方为2.25；
·计算三个值均值再除以2：(0.25+1+2.25)/3/2=0.58(图中第二个五角星所在位置)

·如何看等高线图：

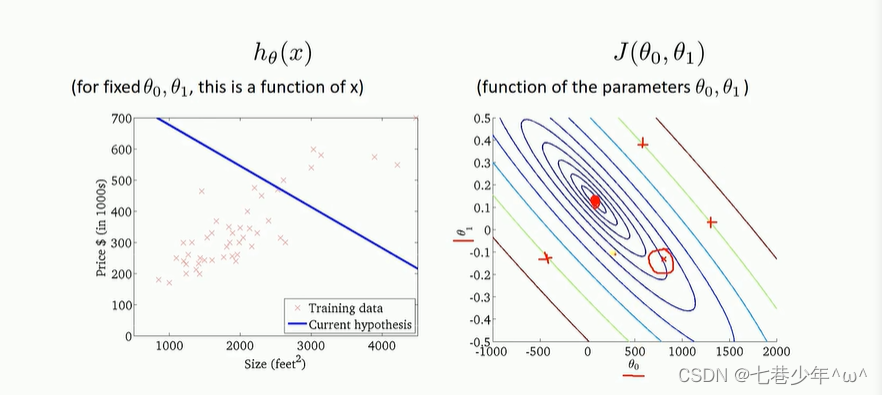
·图中每个圈圈(线条颜色相同)上的值都是相同的，例如3个红色叉叉值是相同的
·中间的实心红点代表图中的最小值，空心红圈越接近实心红点，就是损失函数越小
·空心红圈所对应的代表左侧图像的蓝色线：y轴数值代表左侧图像的斜率，x轴数值代表左侧图像的截距

2.3 相关系数: （R）

1.目的：

衡量线性相关性的强弱（用来描述两个变量之间的线性关系）

2.公式：

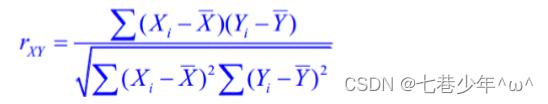
3.结果：

相关系数越接近于1，样本点的分布越接近于线性关系

2.4 决定系数: （R^2）

1.目的：

用来描述非线性或两个及以上自变量的相关关系，也可用于评价模型的效果

2.公式：

1).总平方和: (SST)

参数说明：
𝑦𝑖：真实值的y
y`：真实值的均值

2).回归平方和: (SSR)

参数说明：
y^:预测值的y值
y`：真实值的均值

3).残差平方和: (SSE)

参数说明：
𝑦𝑖：真实值的y
y^:预测值的y值

5).相关系数: (R^2)

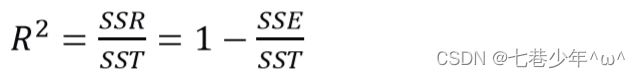
4).SST,SSR,SSE之间的关系:

3.结果：

相关系数越接近于1，样本点的分布越接近于线性关系