一、索引简述

1、什么叫索引

• 索引是数据库中对某一列或多个列的值进行预排序的数据结构。
• 索引可以简单理解为数据的"目录"，使用索引可以快速访问数据表中的特定信息。

2、索引的优缺点

优点：

• 大大加快数据检索的速度。
• 将随机I/O变成顺序I/O(因为B+树的叶子节点是连接在一起的)。
• 加速表与表之间的连接。

缺点：

• 从空间角度考虑，建立索引需要占用物理空间。
• 从时间角度考虑，创建和维护索引都需要花费时间，例如对数据进行增删改的时候都需要维护索引。

3、索引的使用场景

• 对于中大型表建立索引非常有效，对于非常小的表，一般全部表扫描速度更快些。
• 对于超大型的表，建立和维护索引的代价也会变高，这时可以考虑分区技术。
• 如果表的增删改非常多，而查询需求非常少的话，那就没有必要建立索引了，因为维护索引也是需要代价的。
• 一般不会出现再where条件中的字段就没有必要建立索引了。 多个字段经常被查询的话可以考虑联合索引。
• 字段多且字段值没有重复的时候考虑唯一索引。 字段多且有重复的时候考虑普通索引。

二、索引的算法

1、线性查找 Linear Search

事项	说明
时间复杂度	O(N)
算法	从第一个数据开始,逐个匹配
问题	随着数据量的增加，性能会急剧下降

2、二分查找 Binary Search

事项	说明
时间复杂度	O(logN)
算法	1.拿出有序数列中点位置作为比较对象。 2.根据中点数据大小,选取一半数据作为新的数列。 3.每次可以将数据量减小一半。
问题	需要排序；需要确定中点

3、二叉查找树 Binary Search Tree

事项	说明
时间复杂度	O(logN) 或 O(N)
算法	1.使用经典的二叉查找树数据结构。 2.由根节点开始查找。
问题	当根节点一边不断增长，可能退化为线性查找

4、平衡二叉树 AVL Tree

事项	说明
时间复杂度	O(logN)
算法	1.每个节点为单位去读取。 2.查找时,与二叉树搜索树相同。 3. 增删改时,通过旋转操作,维护树的平衡。
问题	AVL树可以保证不会退化成线性查找，

5、B树

事项	说明
时间复杂度	O(mlogmn)
算法	1.B树是线性数据结构和树的结合。 2.B树通过多数据节点大大降低了树的高度。 3. B树不需要旋转就可以保证树的平衡。
问题

6、B+树

事项	说明
时间复杂度	O(mlogmn)
算法	1.由B树发展而来的一种数据结构。 2.B+树的所有数据均在叶子节点。 3. B+树的所有数据形成了一个线性表。
特点	B+树集成了线性表、平衡二叉树的优势

三、B树和B+树的理解

1、B树和B+树的区别

B树和B+树最主要的区别主要有两点：

• B树中的内部节点和叶子节点均存放键和值，而B+树的内部节点只有键没有值，叶子节点存放所有的键和值。
• B＋树的叶子节点是通过相连在一起的，方便顺序检索。
  两者的结构图如下：
  
  

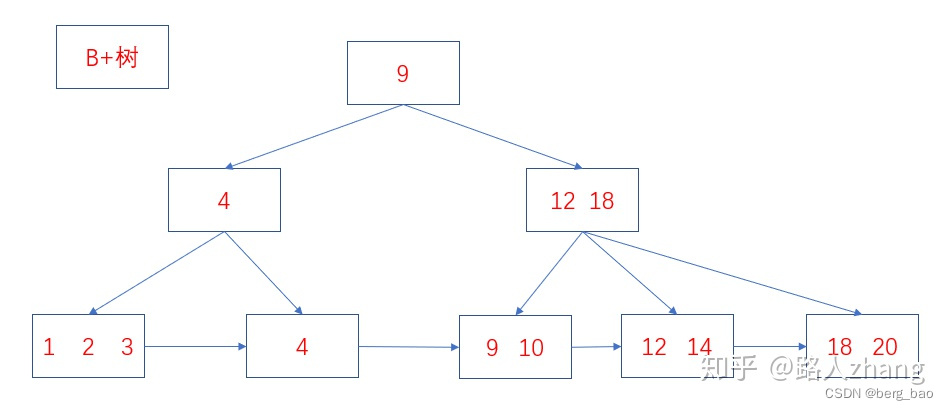
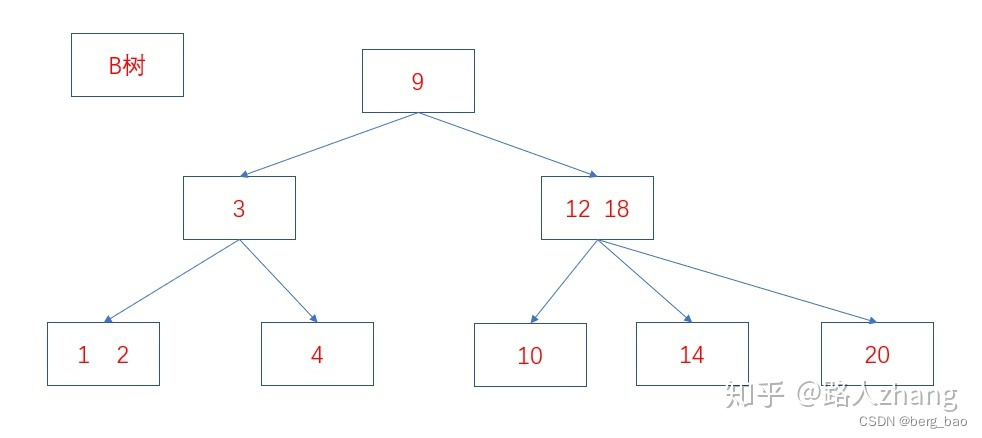
2、数据库为什么使用B+树而不是B树

• B树适用于随机检索，而B+树适用于随机检索和顺序检索
• B+树的空间利用率更高，因为B树每个节点要存储键和值，而B+树的内部节点只存储键，这样B+树的一个节点就可以存储更多的索引，从而使树的高度变低，减少了I/O次数，使得数据检索速度更快。
• B+树的叶子节点都是连接在一起的，所以范围查找，顺序查找更加方便
• B+树的性能更加稳定，因为在B+树中，每次查询都是从根节点到叶子节点，而在B树中，要查询的值可能不在叶子节点，在内部节点就已经找到。
• 那在什么情况适合使用B树呢，因为B树的内部节点也可以存储值，所以可以把一些频繁访问的值放在距离根节点比较近的地方，这样就可以提高查询效率。
• 综上所述，B+树的性能更加适合作为数据库的索引。