问题描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵
平衡 二叉搜索树。

高度平衡的意思是：二叉树是一颗满足“每个结点的左右两个子树的高度差的绝对值不超过1”的二叉树。

示例 1：

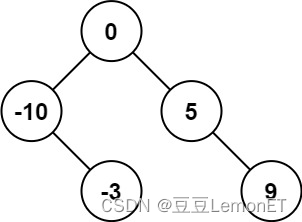
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

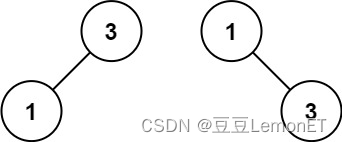
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

解决办法

因为是平衡二叉树，所以总是要选取中间节点，比如在示例一中[-10,-3,0,5,9]，先选取中间节点0，然后再分别同时选取两边数字的左侧[-10,5]或者右侧[-3,9]节点 。

• 中序遍历，总是选择中间位置左边的数字作为根节点
• 中间位置左边的数字作为根节点，则根节点的下标为mid=(left+right)//2
  具体实现步骤：
• 对数组的下标进行遍历，首先排除特殊情况，定义左右边界下标，如果左边的索引大于右边的索引，则返回None
• 第二个特殊情况，如果左右数的索引相等，那么说明只有一个根结点，则建立一个只有根结点的树
• 排除掉这两中情况后，选取中间节点，即mid=[l+r]//2，将其设置为根结点
• 再分别采用递归的方法设置左子树和右子树

代码示例

class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        def arrayToBst(l,r):
            if l > r:
                return None
            if l == r:
                return TreeNode(nums[l],None,None)  #建立一棵树，左、右子树都为空
            else:
                mid = ( l + r ) // 2
                root=TreeNode(nums[mid])
                root.left = arrayToBst(l,mid-1)
                root.right = arrayToBst(mid+1,r)
                return root
        return arrayToBst(0,len(nums)-1)