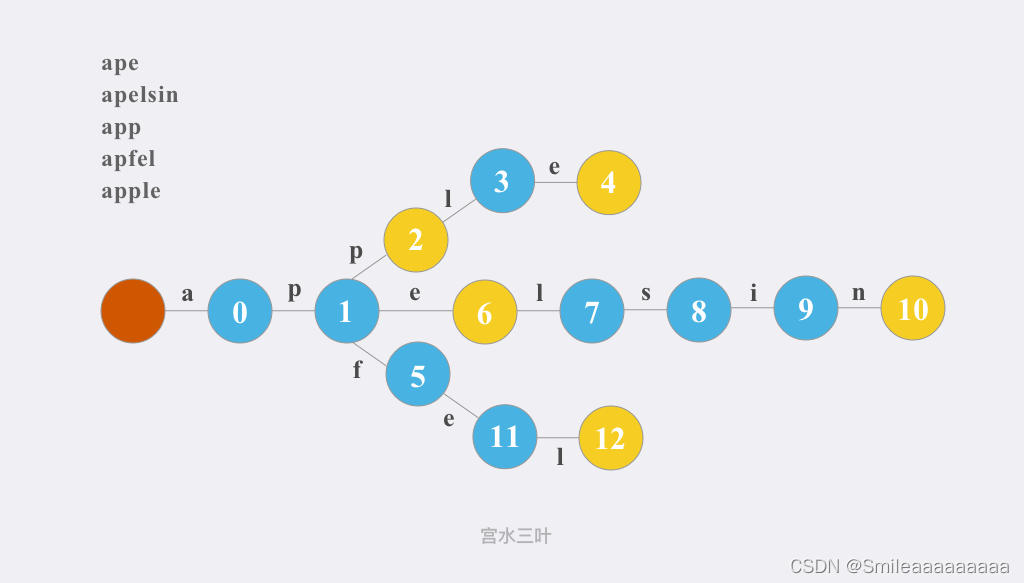
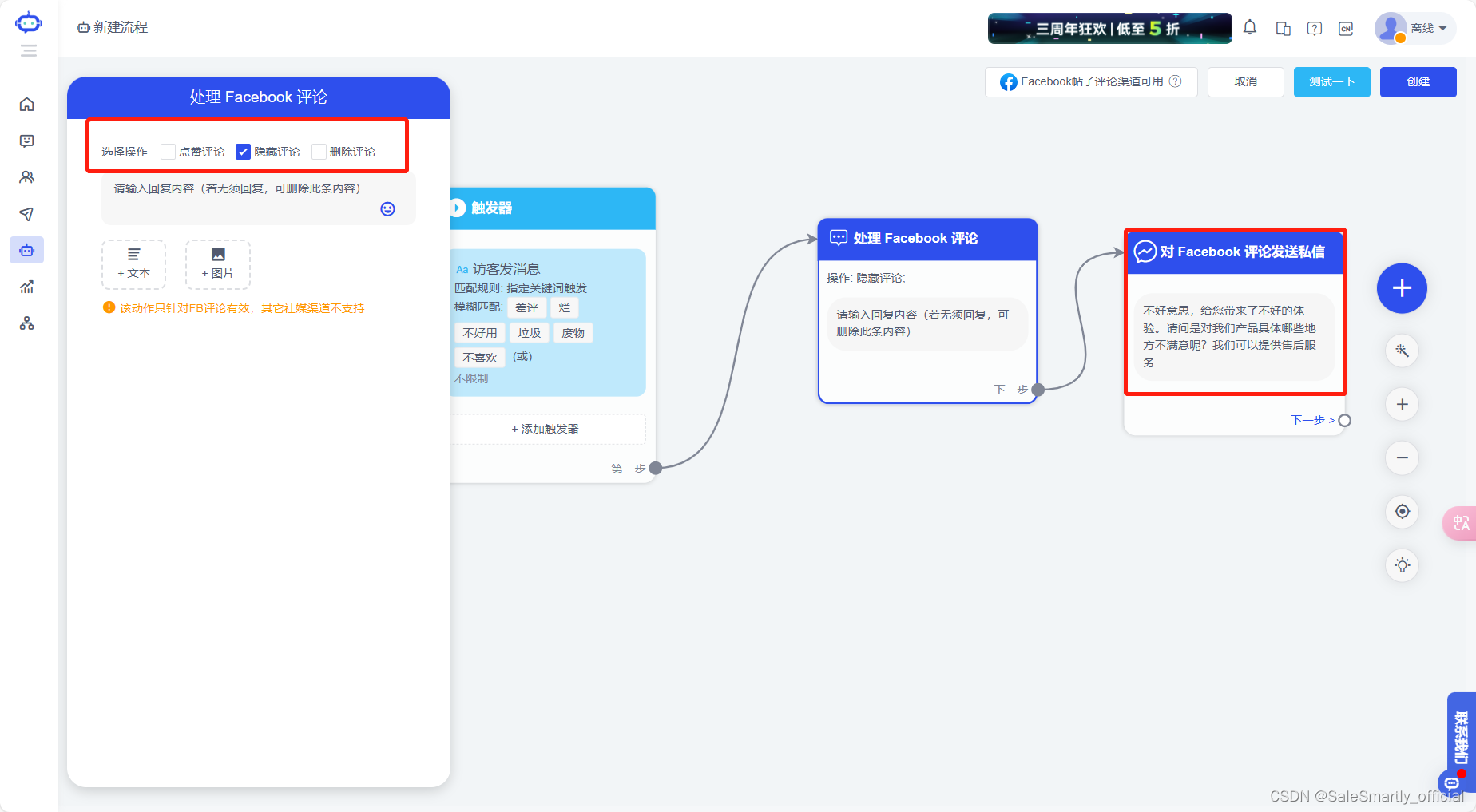
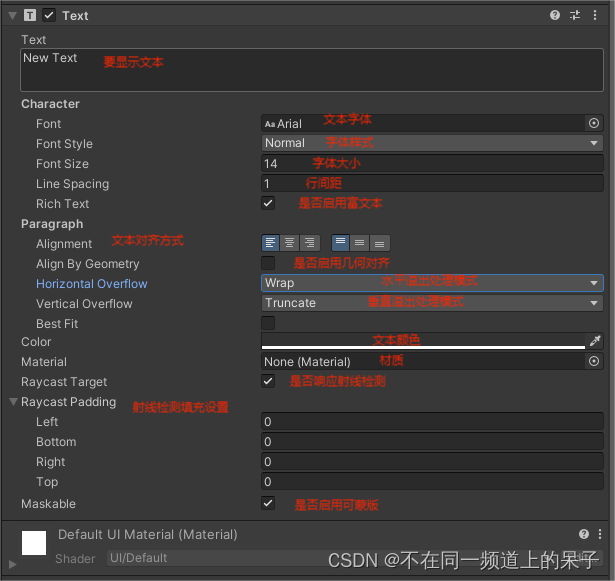
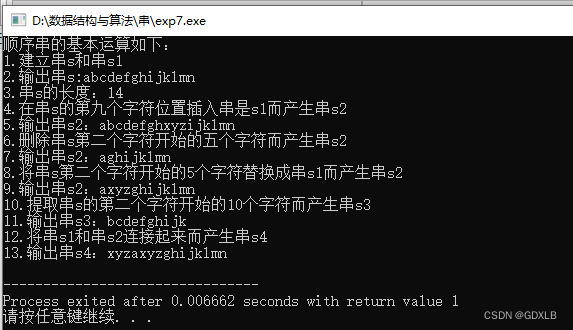
例题——最大上升子序和

分析

• 需要定义状态$dp[i]$，表示前i个元素中，包含第i个元素$a[i]$的最大子序和，则：
  • 若有$j\in [0,i-1]$
    • 当$a[j]<a[i]$时，有$dp[j]+a[i]$有可能是$dp[i]$的值，即$dp[i]=maxdp[j]+a[i]$

代码

#include <cstdio>
#include <string>
#include <map>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <climits>
//#include <bits/stdc++.h>
using namespace std;
int a[1010];
int dp[1010];

int main() {
    int n;
    while(scanf("%d",&n)!=EOF){
        for (int i = 0; i < n; ++i) {
            scanf("%d",&a[i]);
        }
        int ans = INT_MIN;
        for (int i = 0; i < n; ++i) {
            dp[i] = a[i];
            for (int j = 0; j < i; ++j) {
                if (a[j]<a[i]){//可以将i对应值拼到dpj后面
                    dp[i] = max(dp[i],dp[j]+a[i]);
                }
            }
            ans = max(ans,dp[i]);
        }

        printf("%d\n", ans);
    }
    return 0;
}