目录
题目链接:岛屿个数
解题思路:
AC代码(BFS+DFS):
题目链接:岛屿个数
小蓝得到了一副大小为 M×N 的格子地图,可以将其视作一个只包含字符 0(代表海水)和 1(代表陆地)的二维数组,地图之外可以视作全部是海水,每个岛屿由在上/下/左/右四个方向上相邻的 1 相连接而形成。
在岛屿 A 所占据的格子中,如果可以从中选出 k 个不同的格子,使得他们的坐标能够组成一个这样的排列:(x0,y0),(x1,y1),...,(xk−1,yk−1),其中 (x(i+1)%k,y(i+1)%k) 是由 (xi,yi) 通过上/下/左/右移动一次得来的 (0≤i≤k−1),此时这 k 个格子就构成了一个 “环”。
如果另一个岛屿 B 所占据的格子全部位于这个 “环” 内部,此时我们将岛屿 B 视作是岛屿 A 的子岛屿。
若 B 是 A 的子岛屿,C 又是 B 的子岛屿,那 C 也是 A 的子岛屿。
请问这个地图上共有多少个岛屿?
在进行统计时不需要统计子岛屿的数目。
输入格式:
第一行一个整数 T,表示有 T 组测试数据。
接下来输入 T 组数据。
对于每组数据,第一行包含两个用空格分隔的整数 M、N 表示地图大小;接下来输入 M行,每行包含 N 个字符,字符只可能是 0 或 1。
输出格式:
对于每组数据,输出一行,包含一个整数表示答案。
数据范围:
对于 30% 的评测用例,1≤M,N≤10。
对于 100% 的评测用例,1≤T≤10,1≤M,N≤50。
输入样例:
2
5 5
01111
11001
10101
10001
11111
5 6
111111
100001
010101
100001
111111
输出样例:
1
3
样例解释
对于第一组数据,包含两个岛屿,下面用不同的数字进行了区分:
01111
11001
10201
10001
11111
岛屿 2 在岛屿 1 的 “环” 内部,所以岛屿 2 是岛屿 1 的子岛屿,答案为 1。
对于第二组数据,包含三个岛屿,下面用不同的数字进行了区分:
111111
100001
020301
100001
111111
注意岛屿 3 并不是岛屿 1 或者岛屿 2 的子岛屿,因为岛屿 1 和岛屿 2 中均没有“环”。
解题思路:
这不是普通的DFS/BFS搜索题,看着很像最少连通块,但是题目中又有了新的定义就是在陆地环里面(被陆地包围)也算属于此外围岛屿,那么我们就也要判定这种环岛屿,博主的思路是先BFS也可DFS找出连通块的个数(四个方向),建一个vector把连通块的起点存进去,方便去找环岛屿,只要有一个起点(或者此连通块任意一个点),此连通块的点便可通过移动一网打尽,再BFS(或者DFS)判定该岛屿是否属于这种环岛屿,不属于就结果加一,属于就不用加。
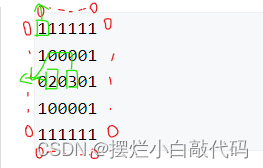
那么如何判断是否输入环岛屿呢,我们观察样例中图,我们把图中外围再加上一圈称为“外海”,我们用vector存了每个连通块的起点,在这个起点上八个方向去DFS(或BFS),只要它达不到外海,说明它肯定被陆地所包围,也就是所说的环岛屿。图中外围都是0(海水),绿色框是每个连通块的起点,此起点只要能达到红色0(外海)就不是环岛屿。图中为2点,无论如何走都到达不了外海。

第二个样例三个起点(绿色框)都可以到达外海,注意判断环岛屿是八个方向,连通块个数是四个方向。
AC代码(BFS+DFS):
#include<iostream>
#include<queue>
#include<cstring>
#include<vector>
using namespace std;
const int N = 55;
typedef pair<int, int> PII;
int T, n, m, res;
int a[N][N],b[N][N];//a为原数组,b为找环岛屿中介数组
char ch[N][N];//输入原数组
bool vis[N][N];//DFS标记数组
bool flag;//是否为环岛屿
vector<PII> v;
int dx[] = { 0,0,1,-1 };//dxdy为遍历岛屿个数
int dy[] = { 1,-1,0,0 };
int dx1[] = { 0,0,1,1,1,-1,-1,-1 };//dx1dy1为遍历岛屿是否为环岛屿
int dy1[] = { 1,-1,1,-1,0,1,-1,0 };
queue<PII> q;
void bfs() {//找岛屿个数
while (q.size()) {
auto t = q.front();
q.pop();
a[t.first][t.second] = 0;
for (int i = 0; i < 4; i++) {
int x = t.first + dx[i];
int y = t.second + dy[i];
if (x <= 0 || y <= 0 || x > m || y > n) {
continue;
}
if (a[x][y] == 0) {
continue;
}
a[x][y] = 0;//不用vis数组,直接自身标记
q.push({ x,y });
}
}
}
void dfs(int x,int y) {//遍历海,是否为环岛屿
if (x == 0 || x == m + 1 || y == 0 || y == n + 1) {
flag = 1;//不是环岛屿
return;
}
for (int i = 0; i < 8; i++) {
int bx = x + dx1[i];
int by = y + dy1[i];
if (bx<0 || bx>m + 1 || by<0 || by>n + 1)continue;
if (b[bx][by] == 1||vis[bx][by])continue;
vis[bx][by] = 1;
dfs(bx, by);
}
}
int main() {
cin >> T;
while (T--) {
cin >> m >> n;
memset(a, 0, sizeof(a));//多组输入,注意初始化
memset(b, 0, sizeof(b));
v.clear();
res = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
cin >> ch[i][j];
a[i][j] = ch[i][j] - '0';
b[i][j] = ch[i][j] - '0';//把原数组复制b一份,这样dfs便可以直接操作
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (a[i][j]) {//是陆地就BFS找此连通块都标记为海洋
q.push({ i,j });
v.push_back({ i,j });//记录起点,dfs找环岛屿用
bfs();
}
}
}
for (auto i : v) {
flag = false;//每一个起点都要初始化
memset(vis, 0, sizeof(vis));
dfs(i.first, i.second);
if (flag==1) {//不是环岛屿
res++;
}
}
cout << res << endl;
}
return 0;
}