文章目录
- 题目
- 前知
- LinkedList和ArryayList
- 组合总和I
- 一、思路
- 二、解题方法
- 三、Code
- 组合总和II
- 一、思路
- 二、解题方法
- 三、Code
- 组合总和III
- 一、思路
- 二、解题方法
- 三、Code
- 总结
先看完上一期组合问题再看这一期更加容易理解喔🤯
在算法和编程的世界中,组合总和问题是一个经典且常见的挑战。LeetCode 平台上的39号、40号和216号题目都涉及到这一问题的不同变体。在本文中,我们将深入研究这些问题,并提供相应的解决方案。
题目
Problem: 39. 组合总和
Problem: 40. 组合总和 II
Problem: 216. 组合总和 III
-
组合总和(Combination Sum):
给定一个无重复元素的数组 candidates 和一个目标数 target,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。 -
组合总和 II(Combination Sum II):
给定一个数组 candidates 和一个目标数 target,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。 -
组合总和 III(Combination Sum III):
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,且每种组合中不存在重复的数字。
前知
LinkedList和ArryayList
ArrayList 和 LinkedList 是 Java 中常用的集合类,用于存储一组元素。它们分别基于动态数组和双向链表实现,具有不同的特点和适用场景。
在 ArrayList 中,add 函数用于在列表的末尾添加元素,remove 函数用于删除指定位置的元素。
在 LinkedList 中,add 函数可以根据需要在列表的任意位置添加元素,remove 函数用于删除指定位置的元素,removeLast 函数用于删除链表的最后一个元素。
ArrayList 是基于数组实现的动态数组。它的特点包括:
- 随机访问:
由于底层是数组,所以 ArrayList 支持通过索引快速访问元素,时间复杂度为 O(1)。
- 尾部操作效率高:
在列表的末尾进行插入和删除操作效率较高,时间复杂度为 O(1)。
- 内存空间连续:
所有的元素在内存中是连续存储的,这样可以利用 CPU 缓存,提高访问速度。
LinkedList 是基于双向链表实现的。它的特点包括:
- 插入和删除效率高:
在任意位置进行插入和删除操作的效率较高,时间复杂度为 O(1)。
- 不支持随机访问:
由于是链表结构,不支持通过索引直接访问元素,只能通过遍历或者迭代器来访问。
- 内存空间不连续:
每个元素在内存中是通过指针相连的,不连续存储,因此对 CPU 缓存的利用率较低。
选择使用哪种集合
1.如果需要频繁地进行随机访问,应该使用 ArrayList。
2.如果需要频繁地进行插入和删除操作,尤其是在列表的中间位置,应该使用 LinkedList。
组合总和I
一、思路
此题的特点是每次递归可以重复选择相同的数字,for循环时startIndex可以不用加1,startIndex就是每次遍历时的位置,详细startIndex含义可以查看上期文章,并且终止条件也没有长度限制,只要元素总和达到结果即可
二、解题方法
回溯三部曲
- 递归函数的返回值以及参数:
确定参数为整数数组,目标值,求和sum,开始遍历的位置startIndex
public void backTracking(int[] candidates,int target,int sum,int startIndex)
- 回溯函数终止条件:
终止条件为求和大于目标值时,退出递归;或者sum等于目标值时,保存path结果到result集合里,退出递归
if(sum > target){
return;
}
if(sum == target) {
result.add(new ArrayList<>(path));
return;
}
- 单层搜索的过程:
for循环横向遍历,保存遍历的元素到path里,求和元素的大小,递归调用,回溯撤销结点,减去sum值
for(int i = startIndex;i < candidates.length;i++){
path.add(candidates[i]);
sum += candidates[i];
backTracking(candidates,target,sum,i);
path.removeLast();
sum -= candidates[i];
}
剪枝优化:
如果提前知道sum求和之后会大于目标值的话,就不需要在进入递归之后再退出递归,此时可以先对数组进行排序,排序之后数组里的值是越来越大的,在保存结点前就判断如果求和之后就已经大于目标值的话,则后面的值递增求和肯定会越来越大,就直接退出本次for循环
//排序
Arrays.sort(candidates);
//大于目标值,退出循环结构
if (sum + candidates[i] > target) break;
三、Code
未进行判断剪枝
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
backTracking(candidates,target,0,0);
return result;
}
public void backTracking(int[] candidates,int target,int sum,int startIndex) {
if(sum > target){
return;
}
if(sum == target) {
result.add(new ArrayList<>(path));
return;
}
for(int i = startIndex;i < candidates.length;i++){
path.add(candidates[i]);
sum += candidates[i];
backTracking(candidates,target,sum,i);
path.removeLast();
sum -= candidates[i];
}
}
}
剪枝优化
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(candidates); // 先进行排序
backtracking(res, new ArrayList<>(), candidates, target, 0, 0);
return res;
}
public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {
// 找到了数字和为 target 的组合
if (sum == target) {
res.add(new ArrayList<>(path));
return;
}
for (int i = idx; i < candidates.length; i++) {
// 如果 sum + candidates[i] > target 就终止遍历
if (sum + candidates[i] > target) break;
path.add(candidates[i]);
backtracking(res, path, candidates, target, sum + candidates[i], i);
path.remove(path.size() - 1); // 回溯,移除路径 path 最后一个元素
}
}
}
组合总和II
一、思路
此题与 组合总和I 唯一的区别就在于剪枝优化后的组合总和基础上多个条件:题目给的整数数组是可重复的。
对什么进行去重:在数组可以重复的情况下,并且要求结果中不能出现重复的组合,例如:组合1[1,2,2],组合2[1,2,2],这就是两个重复的组合。由于candidates可以存在重复元素,就要对结果进行去重,否则会出现重复的组合,去重是针对当前同一层不能出现重复,而一个组合内不同深度之间是可以出现重复元素的,例如组合[1,1,2]中尽管出现了两个1,但是是candidates不同位置上的1,并没有与其它组合重复。所以要判断所在的层前面相同的元素是否使用过,如果使用过,那么存在的所有情况都可以被包含在前面使用过的元素的组合情况里面,相当于是前面元素的组合情况的一个子集,必定会造成重复,所以直接对出现过的元素进行剪枝操作
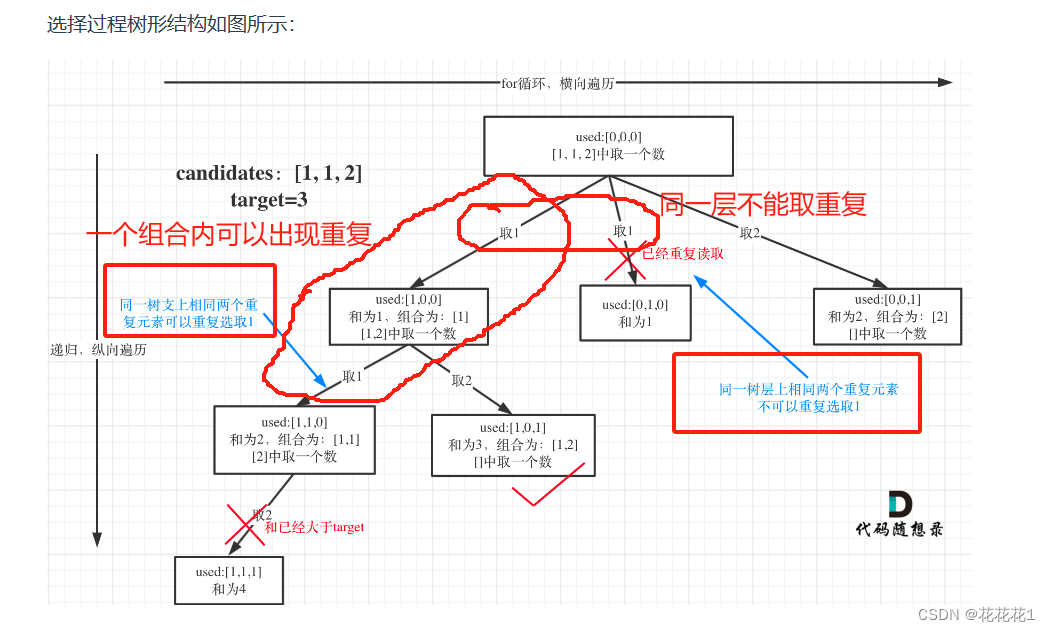
二、解题方法
回溯三部曲
- 递归函数的返回值以及参数:
先对candidates数组进行排序,创建一个used布尔类型的数组,比上面的 组合总和I 多传入一个use数组
public void backTracking(int[] candidates, int target, int sum,int startIndex,boolean[] used)
-
回溯函数终止条件:
终止条件和 组合总和I 相同,略过 -
单层搜索的过程:
在for循环横向遍历时,判断同层是否出现过相同的元素,如果出现过,则跳过该循环,继续横向遍历其它元素,判断逻辑为判断当前元素与前一个元素相同,并且不是纵向的元素重复,如果前一个元素used数组为true的话,说明是在相同元素的下一层重复了,而不是横向同层的重复。每当访问过的元素就让该元素对应的used数组置为true,回溯的话就重新为false。
//去重:同层出现重复结点,直接跳过
if(i>0 && candidates[i] == candidates[i-1] && used[i-1] == false) {
continue;
}
//遍历完之后让used数组为true
used[i] = true;
//回溯为false
used[i] = false;
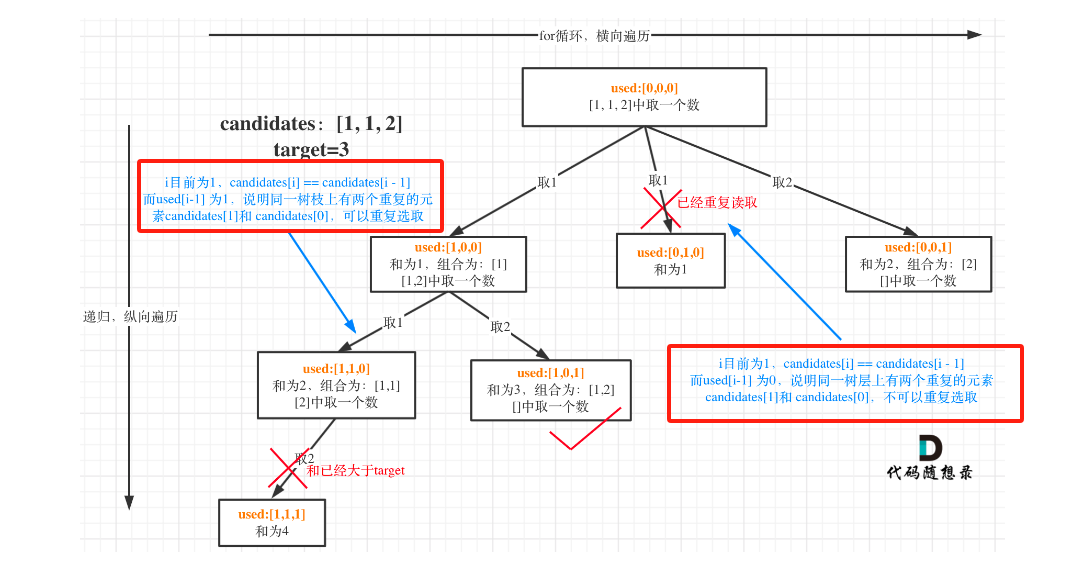
补充:也可以不使用used标记数组记录是否访问过该元素,startIndex也可以直接进行去重
排序之后的数组,当 i>startIndex 时说明已经不是遍历的同层的第一个结点了,至少从第二个结点开始了,而当此时出现元素和前面一个元素相同的情况的话,也就可以直接去重
三、Code
used标记数组记录
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
boolean[] used = new boolean[candidates.length];
Arrays.sort(candidates); // 先进行排序
backTracking(candidates,target,0,0,used);
return result;
}
public void backTracking(int[] candidates, int target, int sum,int startIndex,boolean[] used){
if(sum == target){
result.add(new ArrayList<>(path));
return;
}
for(int i = startIndex;i<candidates.length;i++){
// 剪枝:如果 sum + candidates[i] > target 就终止遍历
if (sum + candidates[i] > target) {
break;
}
//去重:同层出现重复结点,直接跳过
if(i>0 && candidates[i] == candidates[i-1] && used[i-1] == false) {
continue;
}
path.add(candidates[i]);
sum += candidates[i];
used[i] = true;
backTracking(candidates,target,sum,i+1,used);
//回溯
path.removeLast();
sum -= candidates[i];
used[i] = false;
}
}
}
startIndex去重
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates); // 先进行排序
backTracking(candidates,target,0,0);
return result;
}
public void backTracking(int[] candidates, int target, int sum,int startIndex){
if(sum == target){
result.add(new ArrayList<>(path));
return;
}
for(int i = startIndex;i<candidates.length;i++){
// 剪枝:如果 sum + candidates[i] > target 就终止遍历
if (sum + candidates[i] > target) {
break;
}
//去重:同层出现重复结点,直接跳过
if(i>startIndex && candidates[i] == candidates[i-1]) {
continue;
}
path.add(candidates[i]);
sum += candidates[i];
backTracking(candidates,target,sum,i+1);
//回溯
path.removeLast();
sum -= candidates[i];
}
}
}
组合总和III
一、思路
此道题与上一期组合问题非常相似,建议先看一遍上期问题,只多加了判断当叶子结点时是否满足sum和为目标值,并且横向for循环直接定死为[1,2…9],n就可以直接写9。
二、解题方法
回溯三部曲
- 递归函数的返回值以及参数:
输入的参数多了一个整数参数sum用于每遍历一个结点就把值给求和
private void backTracking(int targetSum, int k, int startIndex, int sum)
- 回溯函数终止条件:
终止条件判断当到达叶子结点时sum是否等于目标值,等于就保存到result数组里退出本层递归,不等于就直接退出本层递归;还可以再进行一个剪枝操作,那就是当遍历之后的sum值如果还没到叶子结点之前就已经大于目标值的话,也直接退出本层递归。
if (path.size() == k) {
if (sum == targetSum) result.add(new ArrayList<>(path));
return;
}
if (sum > targetSum) {
return;
}
- 单层搜索的过程:
在把遍历到的数据添加到path里之后,就进行一次求和,递归完了之后,在撤销结点的同时,同样要记得把sum也给减去对应的值。
9 - (k - path.size()) + 1可以查看上期组合问题剪枝优化的操作
三、Code
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
backTracking(n, k, 1, 0);
return result;
}
private void backTracking(int targetSum, int k, int startIndex, int sum) {
// 减枝
if (sum > targetSum) {
return;
}
//终止条件
if (path.size() == k) {
if (sum == targetSum) result.add(new ArrayList<>(path));
return;
}
// 减枝 9 - (k - path.size()) + 1
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
path.add(i);
sum += i;
backTracking(targetSum, k, i + 1, sum);
//回溯
path.removeLast();
//回溯
sum -= i;
}
}
}
总结
以上就是针对这道题的刷题笔记,通过使用回溯法,我们可以有效地解决组合总和问题。对于每个问题,我们都需要仔细考虑题目要求,并编写相应的回溯函数来搜索所有可能的解。在编写代码时,要注意避免重复计算和重复组合的情况,以提高算法的效率。希望本文对你理解和解决组合总和问题有所帮助!🌹