国科大《高级人工智能》沈老师部分——行为主义笔记
- 沈华伟老师yyds,每次上他的课都有一种深入浅出的感觉,他能够把很难的东西讲的很简单,听完就是醍醐灌顶,理解起来特别清晰
- 今年考试题目这部分跟往年基本一样,沈老师画的重点才是真的重点
文章目录
- 一、蚁群优化算法
- 二、粒子群算法
- 三、多臂赌博机
- 四、马尔科夫决策过程
- 五、策略学习
- 六、博弈
- 七、GNN卷积网络
- 八、因果分析
- 考试回忆
一、蚁群优化算法
- 思想:局部随机搜索+自增强
- 基本原理:用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。
蚂蚁依概率选择侯选位置移动,在经过的路径上留下信息素,信息素会随时间挥发,且信息素浓度大的路径更易被选取。 最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解。 - 算法过程:对m只蚂蚁随机放在n个城市,按照公式选择下一个城市的概率,此时公式正比于信息素浓度;
所有蚂蚁周游完后,更新信息素(与路的长度、挥发速度相关); - 适用范围:一种离散的解空间搜索方法,适用于图中找最优路径
二、粒子群算法
-
思想:随机优化
-
基本原理:
- 每个粒子对应于一个可行解,粒子通过位置和速度表示(速度:下一步移动的方向和距离,位置:求解问题的一个解)
- 粒子根据对其他个体信息+位置的评价,更新自己的速度与位置;重复直到粒子群找到问题的最优解
-
算法过程:
-
- 初始化粒子群:随机生成粒子的位置和速度;当前粒子最优位置 全局最优位置
-
- 循环直到满足条件
- ①计算每个粒子的适应度函数
- ②更新每个粒子历史最好适应度+相应位置,更新当前全局最好适应度+位置
- ③更新粒子的速度和位置:速度 = 原速度倾向 + 回到历史最优位置的倾向 + 粒子群全局最优位置的倾向
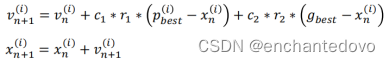
-
-
适用范围:求解连续解空间的优化问题
三、多臂赌博机
- 优化目标:摇固定次数的臂,获得期望累计奖励最大
- 探索与优化关系:利用(即时奖励最大化) + 探索(长期奖励最大化)
- 乐观初值法:为每个行为赋一个高的初始估值,初期每个行为都有较大机会被explore
- UCB:选择潜力大的行为:依据估值的置信上界行为选择(当前估值高+不确定性高)
四、马尔科夫决策过程
- 马尔科夫决策过程:采取行动a转变为下一状态后,获得奖励
- 要素:状态、行为、模型
- 奖励假设:最终目标能通过最大化累计奖励实现
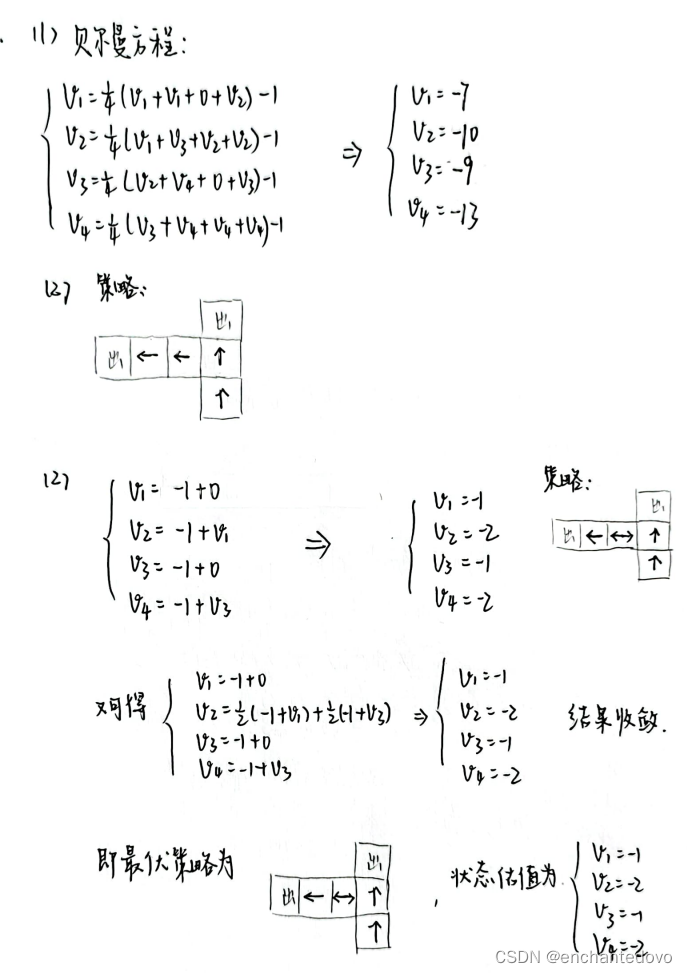
- 贝尔曼方程
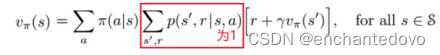
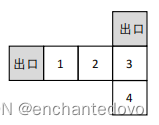
- 格子世界问题(见后)
五、策略学习
动态规划:
- 策略估值:策略=》估值
- 策略提升:根据当前估值=>新策略
- 策略迭代:从初始策略开始,迭代进行策略估值和策略提升,最终得到最优策略
- 估值迭代:从初始状态估值开始,进行估值迭代,找到最优状态估,进而根据最优估值,贪心得到最优策略
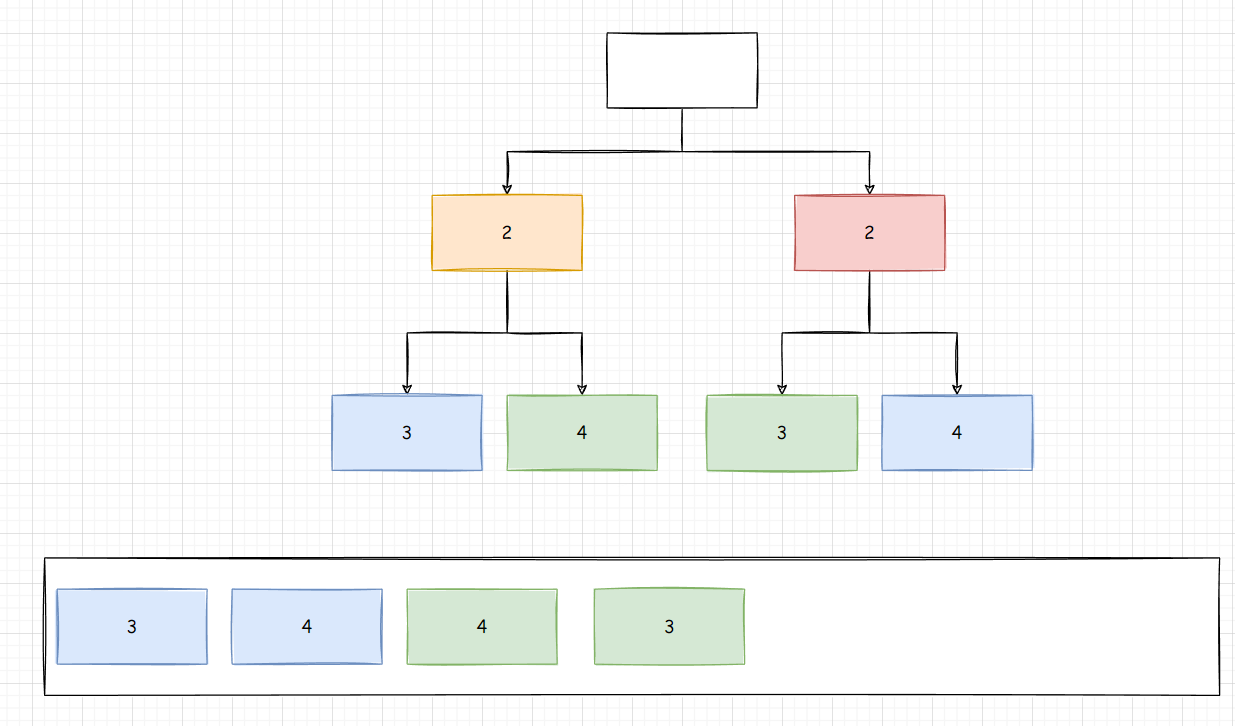
动态规划、蒙特卡洛、时序差分联系和区别(图)
- 动态规划:一层全展开
- 蒙特卡洛:基于经验,一条线
- 暴力搜索:全部展开
- 时序差分:基于经验自举,只有一步的一条线
六、博弈
- 博弈要素:局中人(策略制定者)、策略(可供局中人选择的行动方案)、效用函数(最大化自己的效用)
- 零和博弈:效用函数玩家收益之和为0(剪刀石头布)
- 最佳应对:针对其他人当前策略,自己当前策略优于自己其他策略
- 纳什均衡:相对其他局中人的最佳应对(谁动谁吃亏)
- 社会最优:和最优
- 帕累托最优:至少一人最优
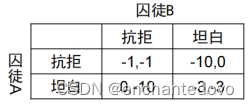
- 囚徒困境:
- 帕累托最优决策组合:(坦白,抗拒),(抗拒,坦白)和(抗拒,抗拒)
- 纳什均衡策略组合:(坦白,坦白)不是帕累托最优
- 社会最优策略组合:(抗拒,抗拒)
- 拍卖:
- 首价:同时提交密封报价,选出价最高以出价购买;最优报价低于估价;人越多,报价越接近估价
- 纳什均衡:每个竞拍者的报价低于其对商品的估价
- 次价:同时提交密封报价,选出价最高以第二高出价购买
- 纳什均衡:每个竞拍者会倾向于采用其对商品的估价进行报价
- 首价:同时提交密封报价,选出价最高以出价购买;最优报价低于估价;人越多,报价越接近估价
- 讨价对象:双方对商品估值之差
- maxmin、minmax策略:
- Maxmin:最大化自己最坏情况下的利益
- minmax:最小化对手最好情况下的利益
- 零和博弈时收益对偶
- 匹配市场:对于z: 7 5 2 - 5 2 0 = 2 3 0,3最大,选b
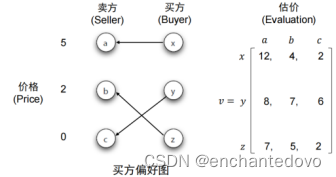
- 议价权
- 稳定结局:未配对的边收益和>=1
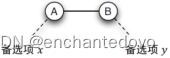
- 纳什议价解:
- 剩余价值:1-x-y
- A收益=(1+x-y)/2
- B收益=(1+y-x)/2
- 均衡结局:任意配对边都满足
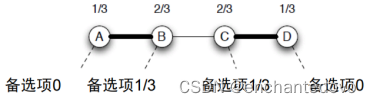
- 备选项:不与当前配对的话,能得到的最大收益
- 稳定结局:未配对的边收益和>=1
七、GNN卷积网络
- spectral谱方法(数学方法)
- 将图的拉普拉斯矩阵的特征向量作为基底,将样本投影到该空间后,进行卷积操作
- 采用超参控制每次选择的相邻节点数量,对变化后的样本做 filter 和求加,再将输出结果进行拉普拉斯的逆变换,并输出非线性化后的结果
- spatial空间方法(计算机方法)
- 从CNN向GCN卷积的k迁移问题在于,需要确定一个固定的邻域,后续卷积的定序、参数共享步骤都可以在确定邻域后解决
- 谱方法可以被定义为空间方法的一个子集
- 相较于空间方法在原始空间定义聚合函数,谱方法在规范后实质上是对变换到新的空间中的样本进行卷积
- 因此谱方法可以被看作是变换空间后的空间方法,其从属于空间方法这一类别。而谱方法将显式地写出了空间变换,空间方法直接将 kernel matrix 定义出来,未写明变换的空间
八、因果分析
d分离问题判断:

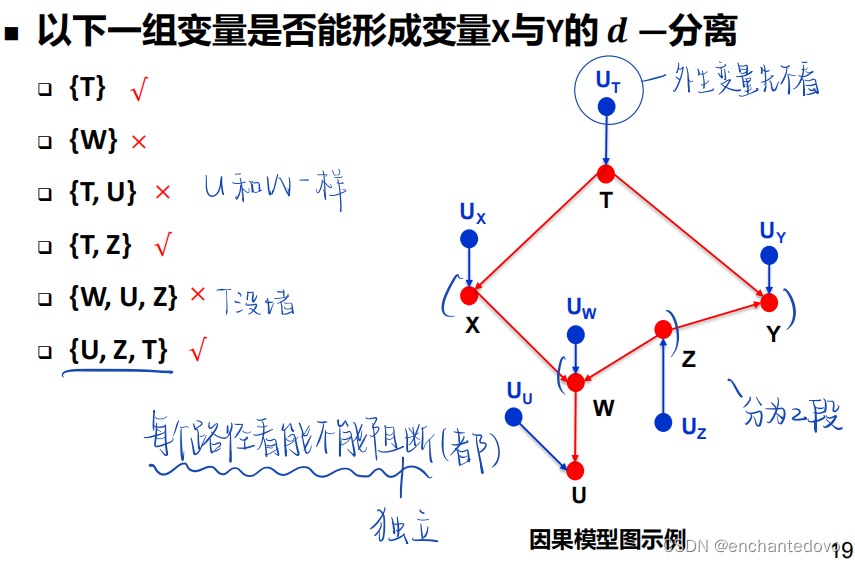
考试回忆
- 选择题:
- 人工智能三大分支
- 图灵测试
- 强化学习状态图选择蒙特卡洛方法
- 囚徒困境帕累托最优
- minmax和maxmin策略
- 图神经网络
- 最优匹配问题
- 因果模型图判断d分离
- 简答题:
- 描述蚁群优化算法 or 粒子群优化算法(万年不变)
- 应用题:
- 格子游戏(万年不变)
- 贝尔曼方程 + 策略提升 + 求解最优策略
- 格子游戏(万年不变)