1.B树和B+树

数据库的大量数据用什么存储？为什么是B树和B+树？使用二叉树不行吗？先来说说他们的演变吧，首先如果用二叉树的话都为排好序的树查询起来是不是效率不高？所以此时我们提出了对树排序，就变成了二叉搜索树，它的性质大家都知道对吧，但是如果考虑极端的情况，我一直插入的数是已经排好序的是不是就会造成"数据倾斜"，也就是说树的高度非常高，也就是退化成了链表的查询，所以我们需要把树变平衡，平衡的概念就是左右子树高度差<=1，于是就提出了平衡二叉树(AVL)和红黑树，前者是严格的完全平衡树，后者是非严格完全平衡树。对于平衡树来说如果海量数据那么树的高度也会非常高，而对于红黑树来说存在极端情况也会出现"数据倾斜"。所以这两者都不适合做数据库索引的结构。出现问题的原因就是只有左右子树，那么如果用多叉树，并且一棵树存储多个节点是不是就可以解决高度很少的情况下存储大量数据。这就引出了B树和B+树。

数据倾斜示意图

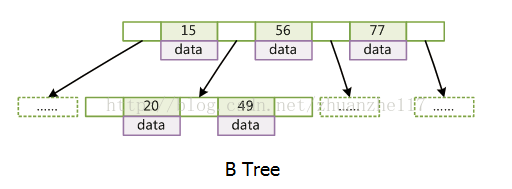
B树结构：

从图中看出几点性质：

1.B树是一个多叉平衡树

2.B树通过二分搜索法可查询数据

3.B树的索引和data存储在一起，并且每一层都存储了索引和data

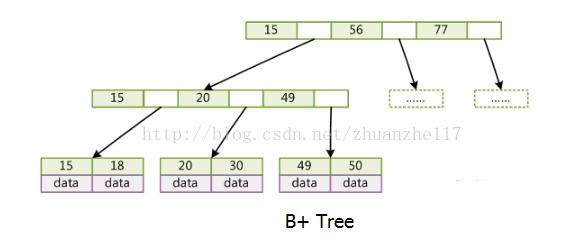
B+树结构：

从图中可得出B+树的性质：

1.B+树也是一个多叉平衡树

2.B+树也可通过二分搜索查询

3.B+树的索引和data分开放，并且data只存放在叶子节点

4.B+树叶子节点使用双向链表相关联

B+树和B树的优化：

1. B+树的索引和数据只存储在叶子节点，而B树每层都存储了data和索引，所以B+树每层可以存储更多的索引，也就是可以存储更多的磁盘数据，磁盘IO次数更加稳定。

2.B+树叶子节点使用的是双向链表相关联，在范围查询是我只需要两个节点即可查询，而B树由于数据在每一层，所以需要遍历整个树，范围查询效率没B+树高。

3.B+树数据都在叶子节点，每次查询的次数都固定的查询复杂度O(longn)，而B树可能在任意一层查询结束，查询不稳定。

4.B+树全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。

B树相对于B+树的优点是，如果经常访问的数据离根节点很近，而B树的非叶子节点本身存有关键字和数据，所以在查询这种数据检索的时候会要比B+树快。

2.AVL树和红黑树

一，AVL树（平衡二叉树）
（1）简介
AVL树是带有平衡条件的二叉查找树，一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡，左右子树的高度差不超过1，和红黑树相比，AVL树是严格的平衡二叉树，平衡条件必须满足（所有节点的左右子树高度差的绝对值不超过1）。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转是非常耗时的，由此我们可以知道AVL树适合用于插入与删除次数比较少，但查找多的情况。
（2）局限性
由于维护这种高度平衡所付出的代价比从中获得的效率收益还大，故而实际的应用不多，更多的地方是用追求局部而不是非常严格整体平衡的红黑树。当然，如果应用场景中对插入删除不频繁，只是对查找要求较高，那么AVL还是较优于红黑树。
（3）应用
1.Windows NT内核中广泛存在;

二、红黑树
（1）简介
一种二叉查找树，但在每个节点增加一个存储位表示节点的颜色，可以是红或黑（非红即黑）。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制，红黑树确保没有一条路径会比其它路径长出两倍（即同一父节点出发到叶子节点，所有路径上的黑色节点数目一样），因此，红黑树是一种弱平衡二叉树，在相同的节点情况下，AVL树的高度低于红黑树，相对于要求严格的AVL树来说，它的旋转次数少，所以对于插入，删除操作较多的情况下，我们就用红黑树。
（2）性质

如图所示，红黑树的特点如下：