1.层序建树
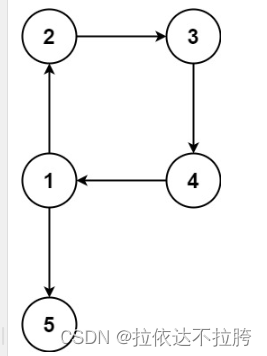
给定一个二叉树的层序遍历序列,空节点用#表示,例如层序序列:“abc##de#g##f###”,其对应二叉树如下图所示:
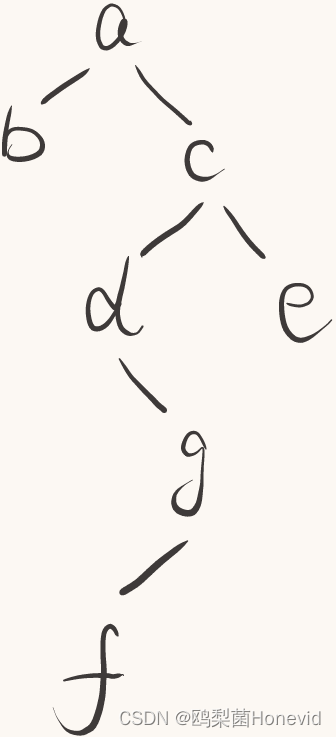
分析
- 创建根节点 TreeNode * root=NULL
- 创建一个队列,用于保存将要插入的位置(先进先出)
- 读取字符:
- 如果不是#,表明是非空结点,创建一个TreeNode对象,把该对象的左右孩子入队;然后判断root是否空
- 若空,直接插入,让root指向新的TreeNode对象
- 非空,访问队列找到本次插入的位置,插入
- 若是#,访问队列,找到本次插入的位置,置为空指针,然后出队
- 如果不是#,表明是非空结点,创建一个TreeNode对象,把该对象的左右孩子入队;然后判断root是否空
代码:
#include <cstdio>
#include <queue>
#include <cmath>
#include <cstring>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
struct treenode {
char data;
treenode *left;
treenode *right;
};
struct queuenode {
treenode *parent;
bool isleftin;
};
//从队列中取出父节点信息并将当前结点信息插入
void construct(treenode *newnode, queue<queuenode *> &myq) {
queuenode *parent = myq.front();
if (parent->isleftin == false) { //左孩子尚未操作
parent->parent->left = newnode;
parent->isleftin = true;
} else {
parent->parent->right = newnode;
myq.pop();
delete parent;//出队后queuenode结点没有利用价值了
}
}
void insert(treenode *&root, queue<queuenode *> &myq, char data) {
if (data != '#') {
treenode *newnode = new treenode;
newnode->data = data;
queuenode *que_member = new queuenode;
que_member->parent = newnode;
que_member->isleftin = false;
myq.push(que_member);
if (root == NULL) {
root = newnode;
} else {
construct(newnode, myq);
}
} else {//是#,插入空节点
if (root != NULL) {
treenode *newnode = NULL;
construct(newnode, myq);
}
}
}
void levelorder(treenode *root) {
queue<treenode *> myq;
myq.push(root);
while (myq.empty() != true) {
treenode *temp = myq.front();
if (temp->left != NULL) {
myq.push(temp->left);
}
if (temp->right != NULL) {
myq.push(temp->right);
}
myq.pop();
printf("%c", temp->data);
}
}
void preorder(treenode *root) {
if (root == NULL) {
return;
}
printf("%c", root->data);
preorder(root->left);
preorder(root->right);
}
int main() {
char list[] = "abc##de#g##f###";
treenode *root = NULL;
queue<queuenode *> myq;
for (int i = 0; i < strlen(list); i++) {
insert(root, myq, list[i]);
}
preorder(root);
printf("\n");
levelorder(root);
return 0;
}
2.先序建树
给定一个二叉树的先序遍历序列,空节点用#表示,例如先序序列:“ab##cd#gf###e##”,其对应二叉树如下图所示:

分析
使用递归的思想:
- 大事化小:
- 读取第一个非#字符:树的根
- 接下来的非#字符:左子树根
- 再接下来的非#字符:右子树根
- 最小问题:读取到#,表明是空树,需要往回走了
代码
#include <cstdio>
#include <queue>
#include <cmath>
#include <cstring>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
struct treenode {
char data;
treenode *left;
treenode *right;
};
void levelorder(treenode *root) {
queue<treenode *> myq;
myq.push(root);
while (myq.empty() != true) {
treenode *temp = myq.front();
if (temp->left != NULL) {
myq.push(temp->left);
}
if (temp->right != NULL) {
myq.push(temp->right);
}
myq.pop();
printf("%c", temp->data);
}
}
void preorder(treenode *root) {
if (root == NULL) {
return;
}
printf("%c", root->data);
preorder(root->left);
preorder(root->right);
}
treenode *pre_build(int &i, char *preord) {
char c = preord[i];
++i;
if (c == '#') {
return NULL;
} else {
treenode *newnode = new treenode;
newnode->data = c;
newnode->left = pre_build(i, preord);
newnode->right = pre_build(i, preord);
return newnode;
}
}
int main() {
char preord[] = "ab##cd#gf###e##";
int i = 0;
treenode *root = pre_build(i, preord);
preorder(root);
printf("\n");
levelorder(root);
return 0;
}
3.先序序列+中序序列建树
给定一个二叉树的先序序列和中序序列,例如abcdgfe(先序)和badfgce(中序),对应的二叉树如下图所示:

分析
仍然采用递归的思想:
设先序序列为preorder[n],中序序列为midorder[n]
- 大事化小:
- 确定根,即树根为preorder[0],左子树为preorder[1~ pos],右子树为preorder[pos+1~ n]
- 找到根,即查询到根preorder[0]在中序序列中的位置为pos,有midorder[0~ (pos-1)]是左子树,midorder[ (pos+1)~n]是右子树
- 最小问题:子树序列长度为0——>表明是空树
代码
#include <cstdio>
#include <queue>
#include <cmath>
#include <cstring>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
struct treenode {
char data;
treenode *left;
treenode *right;
};
void aftervisit(treenode *root) {
if (root == NULL) {
return;
}
aftervisit(root->left);
aftervisit(root->right);
printf("%c", root->data);
}
treenode *rebuild(string pre, string mid) {
if (pre.size() == 0) {
return NULL;
} else {
char root_data = pre[0];
int root_index = mid.find(root_data);
//分割子树
string pre_l = pre.substr(1, root_index);//左子树的pre序列
string pre_r = pre.substr(root_index + 1);//右子树的pre序列
string mid_l = mid.substr(0, root_index);//左子树的mid序列
string mid_r = mid.substr(root_index + 1);//右子树的mid序列
treenode *newnode = new treenode;
newnode->data = root_data;
newnode->left = rebuild(pre_l, mid_l);
newnode->right = rebuild(pre_r, mid_r);
return newnode;
}
}
int main() {
char pre[100];
char mid[100];
scanf("%s\n%s", mid, pre);
treenode *root = rebuild(pre, mid);
aftervisit(root);
return 0;
}
牛刀小试
1. 已知后序序列和中序序列,求前序序列(先自己写一遍再看代码哦)
(我也新建一个文件,重头再练一遍!)
- 输入:badfgce(中序)、bfgdeca(后序)
- 正确结果:abcdgfe(先序)
代码(要诚实!!自己先写一遍!!)
#include <iostream>
using namespace std;
struct treenode {
char data;
treenode *left;
treenode *right;
};
void previsit(treenode *root) {
if (root == NULL) {
return ;
}
printf("%c", root->data);
previsit(root->left);
previsit(root->right);
}
treenode *rebuild(string mid, string aft) {
if (aft.size() == 0) {
return NULL;
} else {
char root_data = aft[aft.size() - 1];
int root_index = mid.find(root_data);
//开始划分子树
string aft_l = aft.substr(0, root_index);
string aft_r = aft.substr(root_index, aft.size() - root_index - 1);
string mid_l = mid.substr(0, root_index);
string mid_r = mid.substr(root_index + 1);
//开始构建子树
treenode *root = new treenode;
root->data = root_data;
root->left = rebuild(mid_l, aft_l);
root->right = rebuild(mid_r, aft_r);
return root;
}
}
int main() {
char mid[100];
char aft[100];
scanf("%s\n%s", mid, aft);
treenode *root = rebuild(mid, aft);
previsit(root);
return 0;
}
注意,我一开始对substr的理解有误,即:将substr函数理解为substr(起始位置序号,尾后序号);(这种理解是错误的),结果会报错:c++ - ‘std::out_of_range’ what(): basic_string::substr: __pos
事实上,substr函数的两个参数是:substr(起始位置序号,分割子串的长度);
解决上述错误的过程中我查阅了两篇文章:
【c++ - ‘std::out_of_range’ what(): basic_string::substr: __pos】
【C++中substr()函数用法详解】
AC纪念墙
这两天把这个HZNU的机试题(网传)刷完了,纪念墙如下
我的感悟是,代码还是要多写,我其实一开始对这里面二叉树的题是有些抗拒的,因此把二叉树的题目留到了最后做,但是回顾了之前写二叉树的代码,死去的回忆重新调入脑袋里面(人脑的缺页异常处理机制哈哈哈),然后感觉也还行,不是很难,就是不练容易忘,牛刀小试时候,重新建立了一个文件,从头开始建二叉树,思路还是很流畅的!!!
我还是蛮厉害的!!!


![[Python] 如何导出PDF文件中的图片](https://img-blog.csdnimg.cn/direct/16265d42e9534caa818210d235dc0de6.png#pic_center)