数据分析思维（三）｜测试/对比思维

news2025/1/16 15:05:48

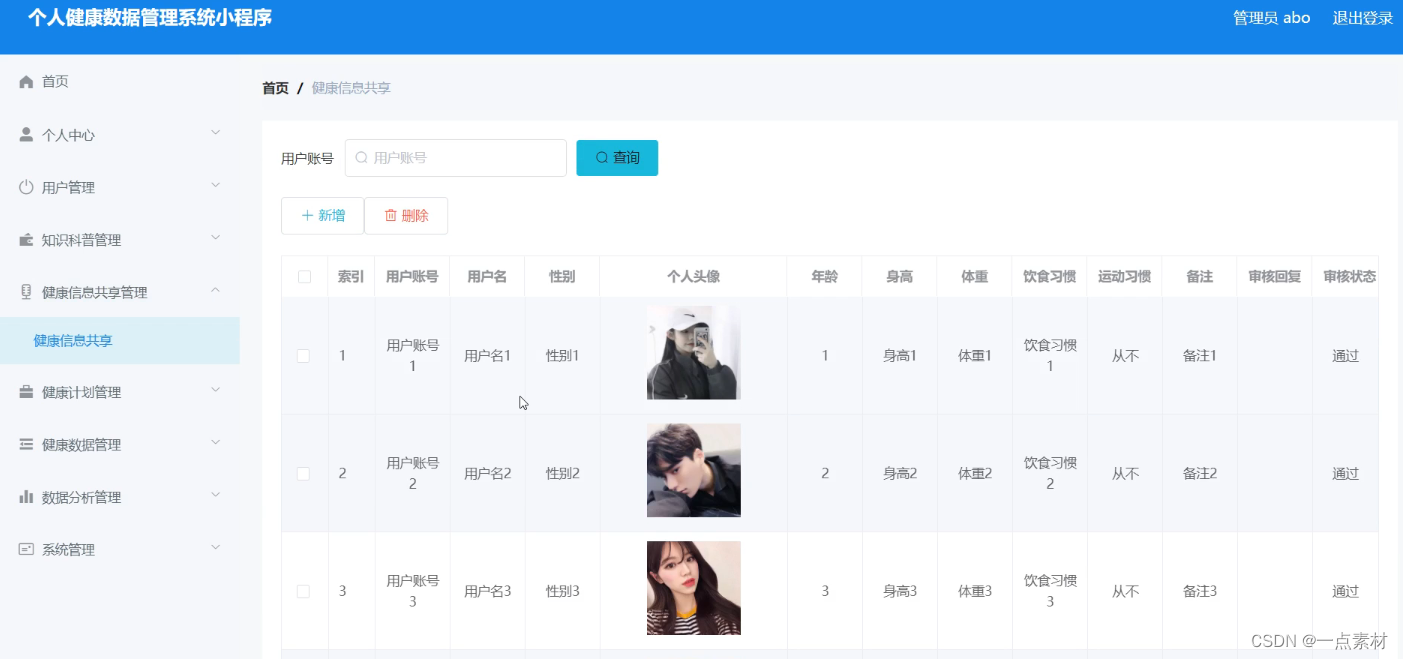
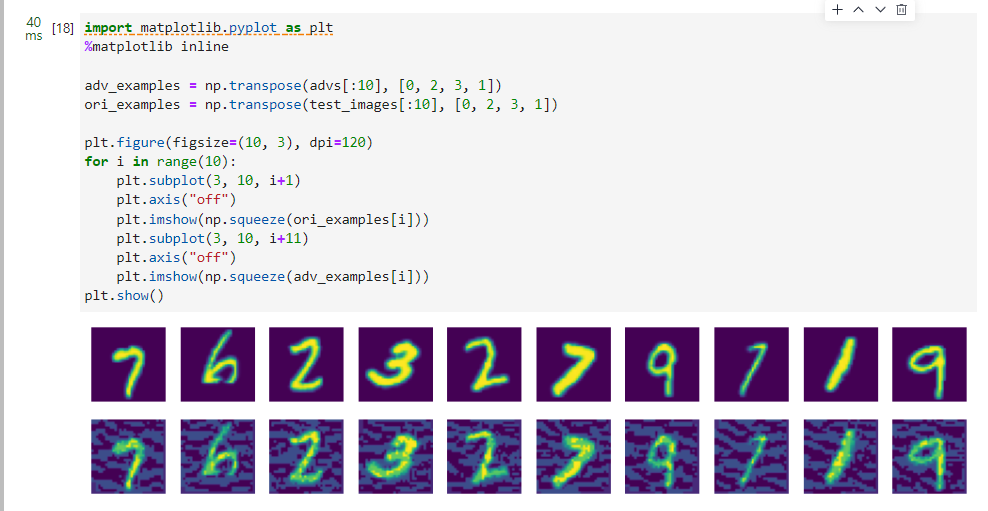
测试/对比思维

1、概念

测试/对比思维可以说在数据分析的工作中随处可见。当我们通过各种手段得到一些结果数据后，如何评价结果的好坏呢？这个时候你可能会想到和标准结果进行比较、和之前的数据进行对照等等方法，这些方法归根结底就是一种测试/对比思维。在该思维中最常用的方法就是A/B测试，本文我们就重点了解一下A/B测试的思想及其应用案例。

2、A/B测试（A/B实验）

为什么要进行A/B测试

在很多互联网软件（广告）想要进行迭代时，通常要先进行假设给出迭代方案，而验证假设是否可行的最好方法就是进行A/B测试。
在进行迭代时，会有想要迭代的目标，比如提高点击率、新用户数、购买转化率等等，我们通常称之为核心指标，A/B测试就是通过观察并计算核心指标的变化最终确定方案是否可行。

A/B测试原理

A/B测试的基本原理为“控制变量法”，我们需要将迭代前的功能（产品）作为对照组，新迭代方案作为实验组，来进行测试。具体需要注意的点如下：
- 保证两个组的人群相同（特征分布一致）；
- 保证实验进行时间相同；
- 保证除了方案变量之外的所有变量都是一致的；
- 可以有多个实验组（A/B实验可以不只有A和B）。

A/B测试的结果判断

前面我们提到过，进行测试时会选择一个核心指标，在相同的环境下对照组和实验组都会产生核心指标，对于二者的指标我们通常采用假设检验的方式来进行判断。（后文会举例说明如何进行判断）
假设检验的方式有很多，通常我们会把A/B测试中的检验分为单样本检验、双样本检验、配对检验三种，对于三种检验方法的使用场景如下：
- 单样本检验：将一组样本和具体的数值进行比较时，为单样本检验。
- 双样本检验：两组随机样本进行比较时，为双样本检验。
- 配对样本检验：将同一组样本前后变化进行比较时，为配对样本检验。
除了检验方法的选择之外，根据样本量和方差是否已知有要选择使用T检验和Z检验。
- 当不知道总体方差时，使用T检验。
- 当总体方差已知，但是样本量<=30时，使用T检验。
- 当总体方差已知，但是样本量>30时，使用Z检验。

A/B测试的流程图

A/B测试的原理看起来很简单，但其难点在于对于环境的控制以及对于方案变量的选择，梳理A/B测试的流程如下图所示：

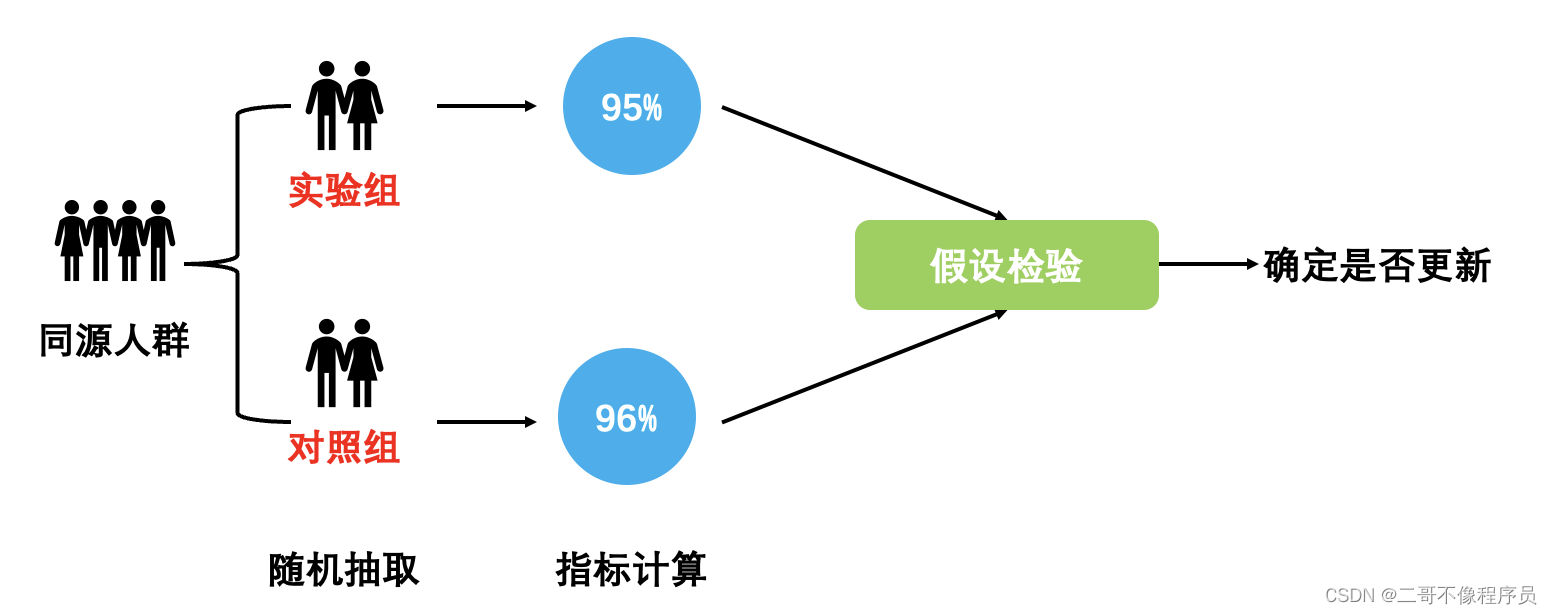
在这里插入图片描述

3、举个例子

某APP为了增加用户粘性，准备更改新的页面风格，为了比较更改前和更改后用户日均使用时长是否有明显差别，我们随机抽取10位用户进行内测并统计其内测前一周（A组）及内侧后一周（B组）的日均使用时长，之后进行A/B测试来进行验证。
数据如下：

	1	2	3	4	5	6	7	8	9	10
A组（min）	80	79	58	90	82	77	74	65	54	70
B组（min）	86	85	60	90	88	84	75	78	58	74

分析：根据上述条件可知，我们进行的是同一组样本前后变化的比较，且样本量<30，因此需要进行配对样本T检验（这里的确定是为了计算时选择对应的检验方式）
做出假设：
- H0：改版前后用户粘性无显著变化。
- H1：改版前后用户粘性有显著变化。

计算P值：

from scipy.stats import ttest_rel
import pandas as pd

x = [80, 79, 58, 90, 82, 77, 74, 65, 54, 70]
y = [86, 85, 60, 90, 88, 84, 75, 78, 58, 74]
# 配对样本t检验
t_val, p = ttest_rel(x, y)
print("P值：", p)

# 结果如下
# P值： 0.0023301816817713405