算法学习16：数论03（容斥原理、博弈论）

---

---

前言

---

提示：以下是本篇文章正文内容：

一、容斥原理：求多个集合的并集

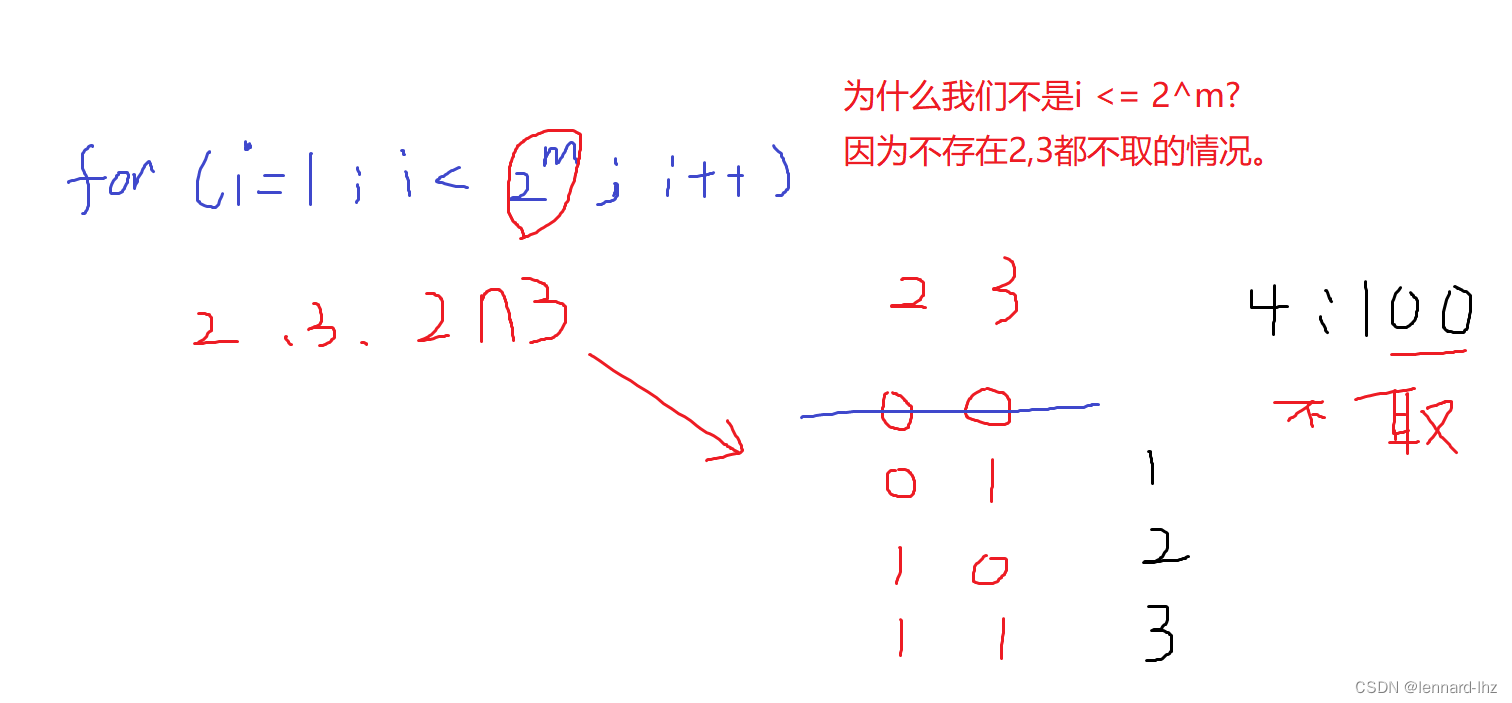
// 例题：给定n和m个不同的质数p1，p2，...，pm
// 请你求出1~n中能被p1，p2，...，pm中至少被一个数整除的有多少个？
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 20;

int n, m;
int p[N];// 存储输入的m个质数 

int main()
{
	cin >> n >> m;
	for(int i = 0; i < m; i ++) cin >> p[i];
	
	int res = 0;
	for(int i = 1; i < 1 << m; i ++)// 循环 2^m-1 次 
	{
		int t = 1, cnt = 0;// t：标志，cnt：判断 奇 还是 偶 集合 
		for(int j = 0; j < m; j ++)
			if(i >> j & 1)
			{
				cnt ++;
				// 分母比分子大，跳 
				if((LL)t * p[j] > n)
				{
					t = -1;
					break;
				}
				t *= p[j];// 计算分母 
			}
		if(t != -1)
		{
			if(cnt % 2) res += n / t;// 奇 正 
			else res -= n / t;// 偶 负 
		}
	}
	cout << res << endl;
	return 0;
 } 

二、博弈论

1.Nim游戏：

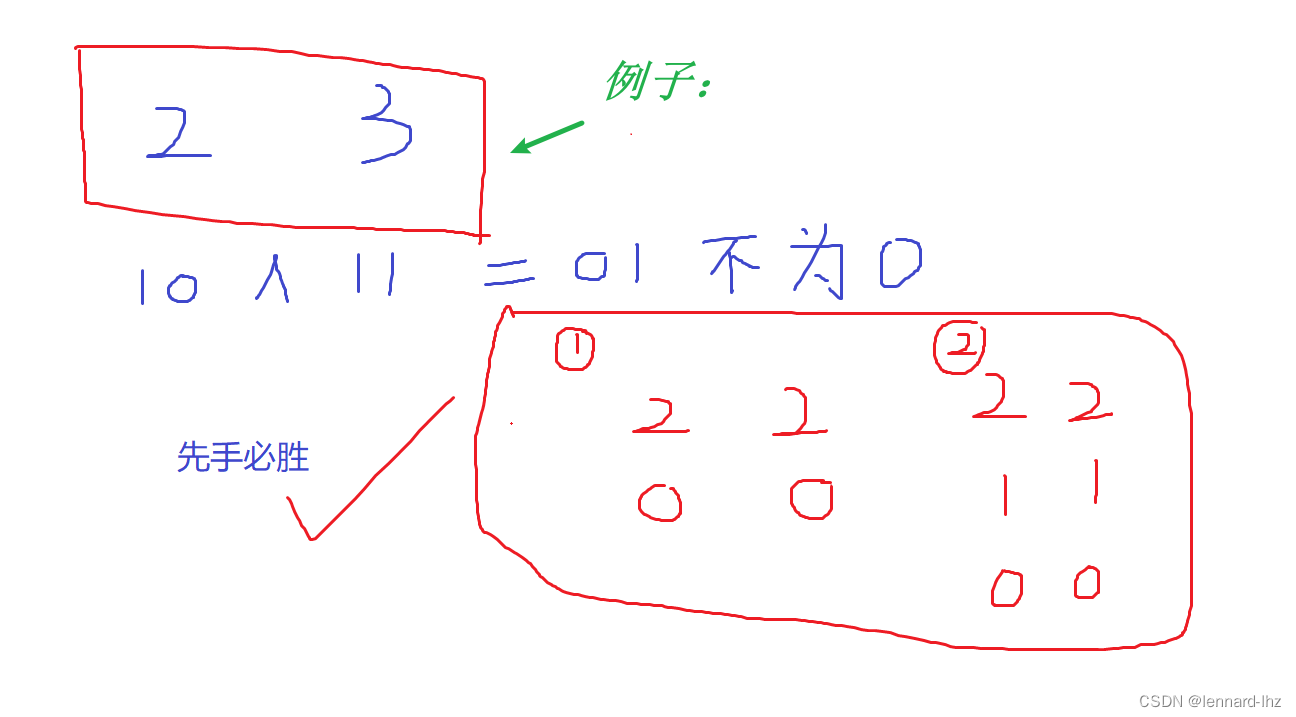
// Nim游戏：给定n堆石子，两位玩家轮流操作，
// 每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），
// 最后无法进行操作的人视为失败。
// 问：如果两人都采用最优策略，先手是否必胜

/*
先手必胜状态：可以走到一个让对手必败的状态 
先手必败状态： 走不到一个可以让自己必胜的状态，找不到对方必败的机会 
*/

/*
输入：第一行包含整数n，第二行包含n个数字，第i个数字表示第i堆石子的数量
输出：Yes，No（能否先手必胜） 
*/

#include <iostream>
#include <algorithm>

using namespace std;

int main()
{
	int n;
	int res = 0;
	
	scanf("%d", &n);
	while(n --)
	{
		int x;
		scanf("%d", &x);
		res ^= x;
	}
	
	if(res) puts("Yes");// 不为0 
	else puts("No");// 为0 
	return 0;
 } 

---

---

2.集合N-im游戏

---

---

---

---

---

---

// 集合-Nim游戏：给定n堆石子和一个有k个不同正整数构成的数字集合S
// 现在两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，
// 每次拿取的石子数量必须包含于集合S，最后无法进行操作的人视为失败
// 问两人都采用最优策略，先手是否必胜

#include <iostream>
#include <algorithm>
#include <cstring>
#include <unordered_set>

using namespace std;

const int N = 110,  M = 10010;

int n, m;
int s[N], f[N];// s：每次拿s[i]个石子，f：记忆化存储 

int sg(int x)
{
	// 记忆化搜索，已经有的元素，直接返回 
	if(f[x] != -1) return f[x];
	
	unordered_set<int> S;// 存储sg（x）可能的情况 
	// x的下一个状态！！！（重点） 
	for(int i = 0; i < m; i ++)
	{
		int sum = s[i];
		if(x >= sum) S.insert(sg(x - sum));
	}
	// mex操作: 
	for(int i = 0; ; i ++)
		if(!S.count(i)) return f[x] = i;
}

int main()
{
	cin >> m;
	for(int i = 0; i < m; i ++) cin >> s[i];
	cin >> n;
	
	memset(f, -1, sizeof f);
	
	int res = 0;
	for(int i = 0; i < n; i ++)
	{
		int x;
		cin >> x;
		res ^= sg(x);// 所有数异或 
	}
	// 不为0：先手必胜 
	if(res) puts("Yes");
	else puts("No");
	return 0;
}

---

---

总结

提示：这里对文章进行总结：

💕💕💕