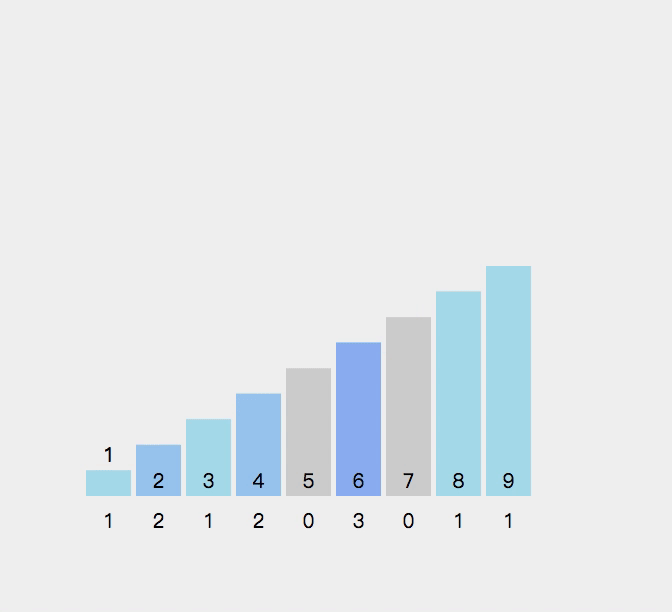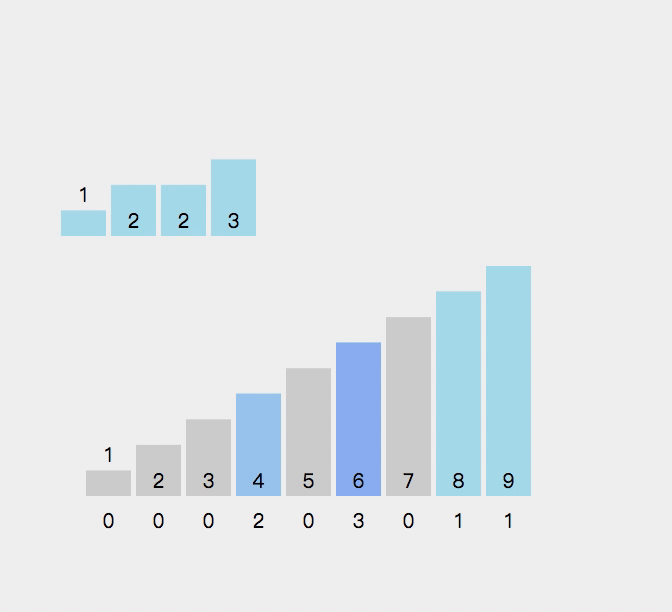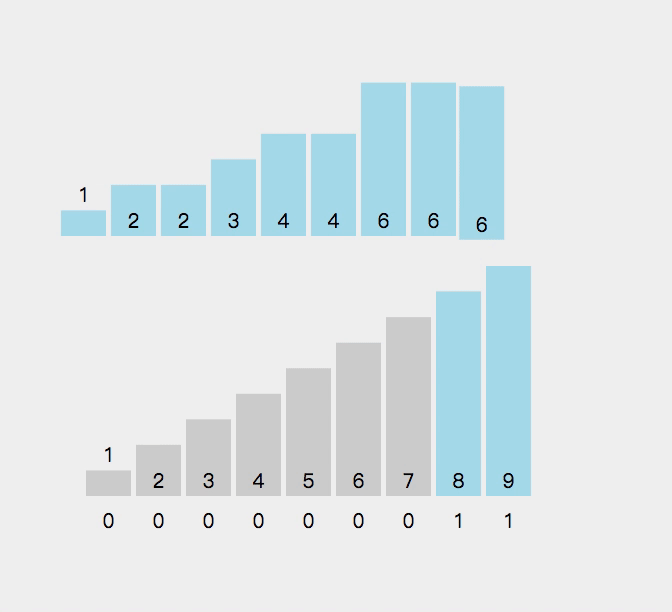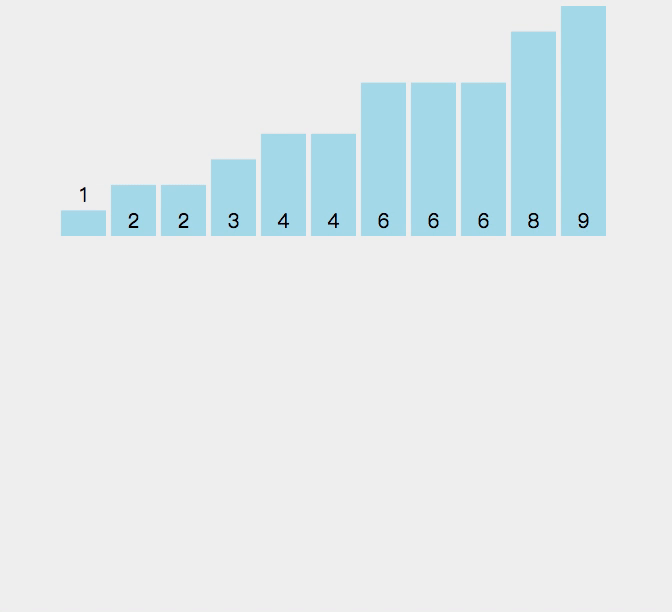介绍
本文用Go将实现二叉搜索树数据结构,以及常见的一些方法
二叉树
二叉树是一种递归数据结构,其中每个节点最多可以有两个子节点。
二叉树的一种常见类型是二叉搜索树,其中每个节点的值都大于或等于左子树中的节点值,并且小于或等于右子树中的节点值。
这是这种二叉树的直观表示:
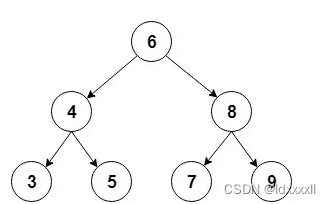
实现细节方面,我们将使用一个辅助Node结构体来存储值,并保留对每个孩子的引用:
type T int
type Node struct {
val T
left *Node
right *Node
}
然后我们将添加树的起始节点,通常称为根:
type BinSearchTree struct {
sync.RWMutex
root *Node
}
常见操作
现在让我们看看我们可以在二叉树上执行的最常见的操作。
插入
我们要介绍的第一个操作是插入新节点。
首先,我们必须找到要添加新节点的位置,以保持树的排序。我们将从根节点开始寻找,遵循这些规则:
- 如果新节点的值小于当前节点的值,我们去左孩子
- 如果新节点的值大于当前节点的值,我们去右孩子
- 如果当前节点为空时,我们到达了一个叶节点,我们可以在该位置插入新节点
然后我们将创建一个递归方法来进行插入:
// insert internal function to find the correct place for a node in a tree
func insert(root, node *Node) {
if node.val < root.val {
if root.left == nil {
root.left = node
} else {
insert(root.left, node)
}
} else {
if root.right == nil {
root.right = node
} else {
insert(root.right, node)
}
}
}
接下来我们将创建从根节点开始递归的公共方法:
// Insert inserts the val in the tree
func (bst *BinSearchTree) Insert(val T) {
bst.Lock()
defer bst.Unlock()
node := NewTree(val)
if bst.root == nil {
bst.root = node
} else {
insert(bst.root, node)
}
}
搜索
现在让我们添加一个方法来检查树是否包含特定值。
和以前一样,我们将首先创建一个遍历树的递归方法:
// search internal recursive function to search t in the tree
func search(root *Node, t T) bool {
if root == nil {
return false
}
if root.val == t {
return true
}
if root.val > t {
return search(root.left, t)
} else {
return search(root.right, t)
}
}
在这里,我们通过将其与当前节点中的值进行比较来搜索该值;然后,我们将根据结果继续左或右孩子。
接下来我们将创建从根开始的公共方法:
// Search returns true if the t exists in the tree
func (bst *BinSearchTree) Search(t T) bool {
bst.RLock()
defer bst.RUnlock()
return search(bst.root, t)
}
删除
另一种常见的操作是从树中删除一个节点。
首先,我们必须以与之前类似的方式找到要删除的节点:
// remove internal recursive function to remove t
func remove(root *Node, t T) {
if root == nil {
return
}
if root.val > t {
remove(root.left, t)
} else if root.val < t {
remove(root.right, t)
} else {
if root.left == nil && root.right == nil {
root = nil
return
} else if root.left == nil {
root = root.right
return
} else if root.right == nil {
root = root.left
return
} else {
leftMostRightSide := root.right
for {
//find the smallest value on the right side
if leftMostRightSide != nil && leftMostRightSide.left != nil {
leftMostRightSide = leftMostRightSide.left
} else {
break
}
}
root.val = leftMostRightSide.val
remove(root.right, root.val)
return
}
}
}
一旦我们找到要删除的节点,主要有 3 种不同的情况:
- 没有孩子:这是最简单的情况;我们只需要在它的父节点中用nil替换这个节点
- 只有一个孩子:在父节点中,我们用它唯一的孩子替换这个节点。
- 有两个孩子:这是最复杂的情况,因为它需要树重组
最后,我们将创建从根开始删除的公共方法:
// Remove removes the t from the tree
func (bst *BinSearchTree) Remove(t T) {
bst.Lock()
defer bst.Unlock()
remove(bst.root, t)
}
遍历树
在本节中,我们将探索遍历树的不同方法,前序、中序和后序遍历,这里暂时只实现递归的方法。
前序
// PreOrder visits all nodes with pre-order traversing
func (bst *BinSearchTree) PreOrder(f func(T)) {
bst.Lock()
defer bst.Unlock()
preOrder(bst.root, f)
}
// preOrder internal recursive function to traverse pre-order
func preOrder(root *Node, f func(T)) {
if root != nil {
f(root.val)
inOrder(root.left, f)
inOrder(root.right, f)
}
}
中序
// InOrder visits all nodes with in-order traversing
func (bst *BinSearchTree) InOrder(f func(T)) {
bst.Lock()
defer bst.Unlock()
inOrder(bst.root, f)
}
// inOrder internal recursive function to traverse in-order
func inOrder(root *Node, f func(T)) {
if root != nil {
inOrder(root.left, f)
f(root.val)
inOrder(root.right, f)
}
}
后序
// PreOrder visits all nodes with pre-order traversing
func (bst *BinSearchTree) PreOrder(f func(T)) {
bst.Lock()
defer bst.Unlock()
preOrder(bst.root, f)
}
// preOrder internal recursive function to traverse pre-order
func preOrder(root *Node, f func(T)) {
if root != nil {
f(root.val)
inOrder(root.left, f)
inOrder(root.right, f)
}
}
其他
本文还提供了一些其他方法,如:
- Max()、Min():获取二叉搜索树中最大或最小值
- Print():打印二叉搜索树
// Min returns the minimal value stored in the tree
func (bst *BinSearchTree) Min() *T {
bst.RLock()
defer bst.RUnlock()
root := bst.root
if root == nil {
return nil
}
for {
if root.left == nil {
return &root.val
}
root = root.left
}
}
// Max returns the maximal value stored in the tree
func (bst *BinSearchTree) Max() *T {
bst.RLock()
defer bst.RUnlock()
root := bst.root
if root == nil {
return nil
}
for {
if root.right == nil {
return &root.val
}
root = root.right
}
}
func (bst *BinSearchTree) Print() {
bst.Lock()
defer bst.Unlock()
fmt.Println("------------------------------------------------")
stringify(bst.root, 0)
fmt.Println("------------------------------------------------")
}
func stringify(root *Node, level int) {
if root != nil {
format := ""
for i := 0; i < level; i++ {
format += " "
}
format += "---[ "
level++
stringify(root.left, level)
fmt.Printf(format+"%d\n", root.val)
stringify(root.right, level)
}
}
单元测试
import (
"testing"
)
const (
t1 T = iota + 1
t2
t3
t4
t5
t6
t7
t8
t9
t10
t11
)
func InitTree() *BinSearchTree {
bst := NewBinSearchTree()
bst.Insert(t3)
bst.Insert(t2)
bst.Insert(t4)
bst.Insert(t9)
bst.Insert(t5)
bst.Insert(t6)
bst.Insert(t10)
bst.Insert(t1)
bst.Insert(t7)
bst.Insert(t8)
return bst
}
func TestBinSearchTree_Insert(t *testing.T) {
bst := InitTree()
bst.Print()
bst.Insert(t11)
bst.Print()
}
func TestBinSearchTree_InOrder(t *testing.T) {
var ret []T
bst := InitTree()
bst.InOrder(func(t T) {
ret = append(ret, t)
})
expected := []T{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
if !isSameSlice(ret, expected) {
t.Errorf("Traversal order incorrect, got %v", ret)
}
}
// isSameSlice returns true if the 2 slices are identical
func isSameSlice(a, b []T) bool {
if a == nil && b == nil {
return true
}
if a == nil || b == nil {
return false
}
if len(a) != len(b) {
return false
}
for i := range a {
if a[i] != b[i] {
return false
}
}
return true
}
部分测试结果:
=== RUN TestBinSearchTree_Insert
------------------------------------------------
---[ 1
---[ 2
---[ 3
---[ 4
---[ 5
---[ 6
---[ 7
---[ 8
---[ 9
---[ 10
------------------------------------------------
------------------------------------------------
---[ 1
---[ 2
---[ 3
---[ 4
---[ 5
---[ 6
---[ 7
---[ 8
---[ 9
---[ 10
---[ 11
------------------------------------------------
--- PASS: TestBinSearchTree_Insert (0.00s)
PASS