📝个人主页:五敷有你
🔥系列专栏:算法分析与设计
⛺️稳中求进,晒太阳

动态规划
概念
- 动态规划法离不开一个关键词,拆分 ,就是把求解的问题分解成若干个子阶段,前一问题的结果就是求解后一问题的子结构。
- 在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。
- 依次解决各子问题,最后一个子问题就是初始问题的解。
适用性
适用动态规划的问题必须满足最优化原理和无后效性。
最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性。
解题思路
1.确定最优子结构:比如我们要求的结果F(X)的最优子结构可能为F(X-1)和F(X-2)
2.列转移方程:根据最优子结构可以列出转移方程F(X)=F(X-1)+F(X-2)
3.确定边界值:确定问题的边界,即当F(n)有可以确定的具体的值
以上概述是纯粹是为了显得官方一点,下面我们开始说人话
动态规划法
确定最优子结构——》列转移方程——》确定边界值
问题
比对两条序列:
YKRDKPHVNIGTIGHVDHGKTTLTAAITSVLAKERGITISTAHVEYQTDKRHYAHIDCPGHADYIKNDGPMPQTREHILLARQVNVPALVVFLNKVDILLELVEMELRELLTEYGFPGDDIPIIKGSALNIMELMD
IGHVDHGKTTLTAAITSVLAKERGITISTAHVIKNMITGAAQMDGAILVVAGTDGPMPQTREHILLARQVNVPALVVFLNKVDIALLELVEMELRELLTEYGFPGDDIPIIKGSALNALNEKAIMELMDAVDDYIP
比对计分策略: p (a, a) = 1 p (a, b) = 0 a != b p (a, -) = p ( -, b) = -1
实验要求:
运行动态规划算法程序,分析四种打分方法的运行结果。
总源码:
# 应用动态规划算法计算比对,得到最佳得分,输出比对序列
# 匹配4,不匹配0,空位-1
def compare(seq_1: str, seq_2: str) -> tuple:
############################
"""
传入两条序列,进行动态规划并返回结果矩阵
Args:
seq_1: 序列1
seq_2: 序列2
Returns:
list_score, list_route:包含得分及路线矩阵的元组
"""
############################
list_route = [[] for i in range(len(seq_1) + 1)] # 路线记录矩阵
list_score = [[] for i in range(len(seq_1) + 1)] # 得分矩阵
# 1 表示当前位置的最优比对路径来源于对角线方向,即 seq_1 和 seq_2 在这个位置匹配。
# 2 表示当前位置的最优比对路径来源于上方,即 seq_1 在这个位置与空位匹配。
# 3 表示当前位置的最优比对路径来源于左侧,即 seq_2 在这个位置与空位匹配。
# 初始化得分矩阵
for row in range(0, len(seq_2) + 1):
for col in range(0, len(seq_1) + 1):
# 在这个特殊情况下,开头的缺失往往有不同的惩罚值,这取决于具体的应用场景和算法设计。
# 在这个代码中,缺失的惩罚值为 -1,表示每引入一个空位扣除1分。
# 表示将seq_2与空位比对的得分。
# 在这个特殊的情况下,第一列的得分矩阵用于表示seq_2中的每个字符与空位之间的比对得分。
# 比对得分是负值,每向下移动一行,得分减小,表示引入了一个空位。
if col == 0:
# 第一列的所有数据都引入一个空位 p (a, -) = p ( -, b) = -1
list_score[row].append(-row)
# 第一列的所有数据都来自上面
list_route[row].append(2)
# 表示将seq_1与空位比对的得分。
# 同样,第一行的得分矩阵用于表示seq_1中的每个字符与空位之间的比对得分。
# 比对得分同样是负值,每向右移动一列,得分减小,表示引入了一个空位
elif row == 0:
list_score[0].append(-col)
list_route[0].append(3)
else:
# 对于不匹配的情况,将得分矩阵的相应位置设置为0。,先是默认全是0
# 二位矩阵的[row][col]添加0
list_score[row].append(0)
list_route[row].append(0)
# 开始计算得分和路径
vacancy = -1 #vacancy空缺就开始惩罚 p(a, -) = p( -, b) = -1
for row in range(1, len(seq_2) + 1):
for col in range(1, len(seq_1) + 1):
if seq_1[col - 1] == seq_2[row - 1]:
temp = 1 # p(a, a) = 4
else:
temp = 0 # p(a, b) = 0 a != b
# 打分
score = list_score[row - 1][col - 1] + temp
if score >= list_score[row - 1][col] + vacancy and score >= list_score[row][col - 1] + vacancy:
list_score[row][col] = score
# 得分来自斜对面
list_route[row][col] = 1
# 表示从上方的位置引入一个空位,并且计算得分。
elif list_score[row - 1][col] >= list_score[row][col - 1]:
list_score[row][col] = list_score[row - 1][col] + vacancy
# 得分来自上面
list_route[row][col] = 2
# 表示从左方的位置引入一个空位,并且计算得分。
else:
list_score[row][col] = list_score[row][col - 1] + vacancy
# 得分来自上面左边
list_route[row][col] = 3
return list_score, list_route
def output(seq_1: str, seq_2: str, score: list, route: list) -> None:
##########################
"""
根据传入的数据输出最佳得分和比对序列结果
Args:
seq_1: 序列1
seq_2: 序列2
score: 得分矩阵
route: 路线矩阵
Returns:
None
"""
##########################
# 在这个上下文中,align_1 和 align_2 是用来表示比对序列的字符串。这两个字符串的构建是通过动态规划算法的回溯过程获得的,用来展示两个输入序列在比对中的对应关系。
# 这两个字符串的构建是通过动态规划算法回溯的过程中的选择和记录,最终呈现出了比对的结果。在比对结果中,这两个字符串的相应位置表示对应序列的匹配或空位。
# align_1:表示比对后的第一个序列。在比对中,可能会有空位('-')和与另一个序列匹配的字符。这个字符串记录了第一个序列在比对中的情况。
align_1 = ""
# align_2:表示比对后的第二个序列。同样,可能包含空位和与另一个序列匹配的字符。这个字符串记录了第二个序列在比对中的情况。
align_2 = ""
# locate 是用来表示比对序列中的匹配和不匹配的标记字符串。
# 在 output 函数中,locate 的构建是通过比对 align_1 和 align_2 中的字符来判断是否匹配。
# 如果两个字符相同,就用 "|" 表示匹配,否则用空格表示不匹配。
locate = ""
row = len(seq_2)
col = len(seq_1)
best = score[row][col]
while True:
if row == 0 and col == 0:
break
#如果 list_route[row][col] 的值为 1,说明当前位置的最优路径来源于对角线,即 seq_1 和 seq_2 在这个位置匹配。
# 因此,在比对序列 align_1 和 align_2 的过程中,将当前位置的字符添加到两个序列中,并向左上角移动一步。
if route[row][col] == 1:
align_1 += seq_2[row - 1]
align_2 += seq_1[col - 1]
row -= 1
col -= 1
# 如果 list_route[row][col] 的值为 2,说明当前位置的最优路径来源于上方,即 seq_1 在这个位置与空位匹配。
# 在比对序列的过程中,将当前位置的 seq_2 中的字符添加到 align_1 中,同时在 align_2 中添加一个空位('-'),然后向上移动一步。
elif route[row][col] == 2:
align_1 += seq_2[row - 1]
align_2 += "-"
row -= 1
# best的前驱是左角
# 如果list_route[row][col]的值为3,说明当前位置的最优路径来源于左侧,即seq_2在这个位置与空位匹配。
# 在比对序列的过程中,将当前位置的seq_1中的字符添加到align_2中,同时在align_1中添加一个空位('-'),然后向左移动一步。
else:
align_1 += "-"
align_2 += seq_1[col - 1]
col -= 1
# 这是在进行对比 好看
for index in range(0, len(align_1)):
if align_1[index] == align_2[index]:
locate += "|"
else:
locate += " "
# 输出结果
print(f"The best score is: {best}")
print(f"Alignment sequences:")
print(f"{align_2[::-1]}\n{locate[::-1]}\n{align_1[::-1]}")
# Main Program
fir_seq = "YKRDKPHVNIGTIGHVDHGKTTLTAAITSVLAKERGITISTAHVEYQTDKRHYAHIDCPGHADYIKNDGPMPQTREHILLARQVNVPALVVFLNKVDILLELVEMELRELLTEYGFPGDDIPIIKGSALNIMELMD"
sec_seq = "IGHVDHGKTTLTAAITSVLAKERGITISTAHVIKNMITGAAQMDGAILVVAGTDGPMPQTREHILLARQVNVPALVVFLNKVDIALLELVEMELRELLTEYGFPGDDIPIIKGSALNALNEKAIMELMDAVDDYIP"
result = compare(fir_seq, sec_seq)
output(fir_seq, sec_seq, result[0], result[1])
第一部分代码
def compare(seq_1: str, seq_2: str) -> tuple:
#####################
"""
传入两条序列,进行动态规划并返回结果矩阵
Args:
seq_1: 序列1
seq_2: 序列2
Returns:
list_score, list_route:包含得分及路线矩阵的元组
"""
#####################
#为二位数组申请空间
list_route = [[] for i in range(len(seq_1) + 1)] # 路线记录矩阵
list_score = [[] for i in range(len(seq_1) + 1)] # 得分矩阵
# 1 表示当前位置的最优比对路径来源于对角线方向,即 seq_1 和 seq_2 在这个位置匹配。
# 2 表示当前位置的最优比对路径来源于上方,即 seq_1 在这个位置与空位匹配。
# 3 表示当前位置的最优比对路径来源于左侧,即 seq_2 在这个位置与空位匹配。
# 初始化得分矩阵
for row in range(0, len(seq_2) + 1):
for col in range(0, len(seq_1) + 1):
if col == 0:
#第一列的所有数据每引入一个空位罚分-1 p (a, -) = p ( -, b) = -1
list_score[row].append(-row)
#第一列的所有数据都来自上面
list_route[row].append(2)
elif row == 0:
#第一行的所有数据来自左边,每引入一个空位罚分 -1
list_score[0].append(-col)
list_route[0].append(3)
else:
#0 暂时做一个占位符
list_score[row].append(0)
list_route[row].append(0)
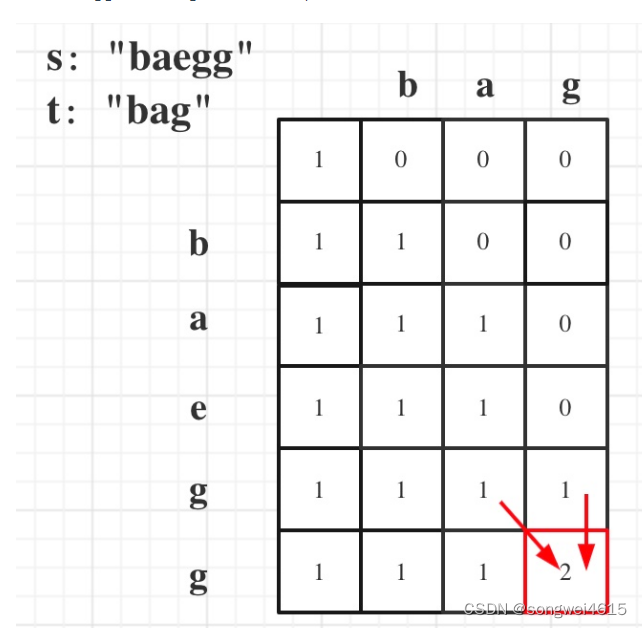
运行到这的结果是如下
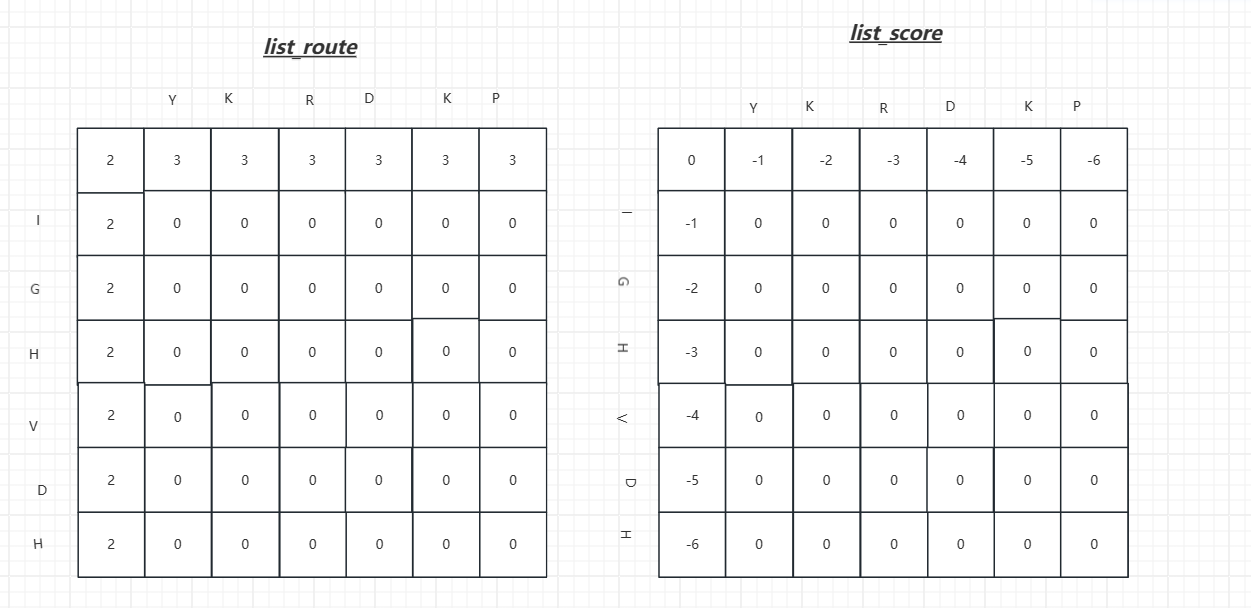
接下来开始计算得分与路径
# 开始计算得分和路径
vacancy = -1 #vacancy空位就开始惩罚 p(a, -) = p( -, b) = -1
for row in range(1, len(seq_2) + 1):
for col in range(1, len(seq_1) + 1):
if seq_1[col - 1] == seq_2[row - 1]:
temp = 4 # p(a, a) = 4
else:
temp = 0 # p(a, b) = 0 a != b
# 打分
score = list_score[row - 1][col - 1] + temp
if score >= list_score[row - 1][col] + vacancy and score >= list_score[row][col - 1] + vacancy:
list_score[row][col] = score
# 得分来自斜对面
list_route[row][col] = 1
# 表示从上方的位置引入一个空位,并且计算得分。
elif list_score[row - 1][col] >= list_score[row][col - 1]:
list_score[row][col] = list_score[row - 1][col] + vacancy
# 得分来自上面
list_route[row][col] = 2
# 表示从左方的位置引入一个空位,并且计算得分。
else:
list_score[row][col] = list_score[row][col - 1] + vacancy
# 得分来自上面左边
list_route[row][col] = 3
return list_score, list_route
结果如下:

开始回溯构建align_1 和 align_2
他们 是用来表示比对序列的字符串。这两个字符串的构建是通过动态规划算法的回溯过程获得的,用来展示两个输入序列在比对中的对应关系。
- align_1:表示比对后的第一个序列。在比对中,可能会有空位('-')和与另一个序列匹配的字符。这个字符串记录了第一个序列在比对中的情况。
- align_2:表示比对后的第二个序列。同样,可能包含空位和与另一个序列匹配的字符。这个字符串记录了第二个序列在比对中的情况。
这两个字符串的构建是通过动态规划算法回溯的过程中的选择和记录,最终呈现出了比对的结果。在比对结果中,这两个字符串的相应位置表示对应序列的匹配或空位
def output(seq_1: str, seq_2: str, score: list, route: list) -> None:
##########################
"""
根据传入的数据输出最佳得分和比对序列结果
Args:
seq_1: 序列1
seq_2: 序列2
score: 得分矩阵
route: 路线矩阵
Returns:
None
"""
##########################
align_1 = ""
align_2 = ""
locate = ""
row = len(seq_2)
col = len(seq_1)
best = score[row][col]
while True:
if row == 0 and col == 0:
break
#如果 list_route[row][col] 的值为 1,说明当前位置的最优路径来源于对角线,即 seq_1 和 seq_2 在这个位置匹配。
# 因此,在比对序列 align_1 和 align_2 的过程中,将当前位置的字符添加到两个序列中,并向左上角移动一步。
if route[row][col] == 1:
align_1 += seq_2[row - 1]
align_2 += seq_1[col - 1]
row -= 1
col -= 1
# 如果 list_route[row][col] 的值为 2,说明当前位置的最优路径来源于上方,即 seq_1 在这个位置与空位匹配。
# 在比对序列的过程中,将当前位置的 seq_2 中的字符添加到 align_1 中,同时在 align_2 中添加一个空位('-'),然后向上移动一步。
elif route[row][col] == 2:
align_1 += seq_2[row - 1]
align_2 += "-"
row -= 1
# 如果list_route[row][col]的值为3,说明当前位置的最优路径来源于左侧,即seq_2在这个位置与空位匹配。
# 在比对序列的过程中,将当前位置的seq_1中的字符添加到align_2中,同时在align_1中添加一个空位('-'),然后向左移动一步。
else:
align_1 += "-"
align_2 += seq_1[col - 1]
col -= 1构建locate
locate 是用来表示比对序列中的匹配和不匹配的标记字符串。在 output 函数中,locate 的构建是通过比对 align_1 和
align_2 中的字符来判断是否匹配。如果两个字符相同,就用 "|" 表示匹配,否则用空格表示不匹配。
# 这是在进行对比 好看
# 这是在进行对比 好看
for index in range(0, len(align_1)):
if align_1[index] == align_2[index]:
locate += "|"
else:
locate += " "
输出结果即可
# 输出结果
print(f"The best score is: {best}")
print(f"Alignment sequences:")
print(f"{align_2[::-1]}\n{locate[::-1]}\n{align_1[::-1]}")
可能遇到的问题
为什么每向下移动一行,得分减小
在这个动态规划比对算法中,得分矩阵的初始化是为了考虑序列的开头与空位(gap)之间的比对得分。具体来说,得分矩阵的第一列对应着将 seq_2 与空位比对的得分。
比对下面的逻辑:
- 匹配:
当序列中的字符匹配时,得分增加。在这个算法中,匹配的得分为4,因此对角线方向的得分会比上方或左方高。
- 缺失(引入空位):
当序列中的字符与空位匹配时,得分减小。在这个算法中,引入空位的惩罚值为-1,因此每引入一个空位,得分就减小1。
所以,得分矩阵的第一列是为了表示 seq_2 中的每个字符与空位之间的比对得分。由于引入了空位,因此每向下移动一行,就意味着在 seq_2 中引入了一个空位,从而得分减小。这种初始化反映了在比对序列的开头时引入空位的惩罚,因为通常在序列的开头引入空位可能导致整体比对得分下降。
结果分析
1. The best score is: 75
- 这里的 "75" 是比对的最佳得分。在你的比对算法中,得分是根据匹配和不匹配的规则计算得出的。这个得分表示在最优比对路径下,两个序列之间的相似性。
2.Alignment sequences:
- 这部分显示了两个比对的序列,其中 "-" 表示引入了空位。
- align_1
- align_2
3.“ | ”
- 这一行是比对序列的标记,"|" 表示对应的位置上,两个序列的字符是匹配的。
所以,这个比对的结果告诉你,通过引入空位,"YKRDKP" 和 "IGHVDH" 在某些位置上可以比对,而得分为2是在最优路径下的相似性得分。比对的结果表明,在比对的过程中,第一个序列中的字符 "Y" 与第二个序列中的字符 "I" 不匹配,并且在 "IGHVD-H" 的比对序列中引入了一个空位。
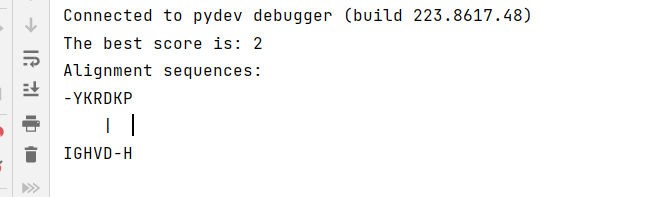
最佳得分概念、总长度,序列长度,
"最佳得分" 是比对算法计算的最优比对的得分,表示两个序列之间的相似性。
- "总长度" 是指比对后的序列总长度。这个总长度包括了引入的空位以及匹配的字符。
- "序列长度" 则是原始未比对的两个输入序列中较长的那个的长度。这个值是不变的,因为它只考虑了原始序列的长度而不考虑比对。
在比对过程中,为了使两个序列对齐,可能需要在某些位置引入空位。这就导致了比对后的序列长度会大于原始序列的长度。在你的结果中,"引入空位" 的值为 16,表示在比对的过程中引入了16个空位,因此 "总长度" 为 "序列长度" 加上引入的空位数。
同时, "匹配数目" 为 105,表示在比对的过程中有105个位置的字符是匹配的。这些匹配的字符会占据 "总长度" 的一部分。
结果

为什么斜着走也开空位了没有惩罚?
因为斜着走没有引入空位,下面这段代码在进行总长度的序列拼接时并没有引入空位
#如果 list_route[row][col] 的值为 1,说明当前位置的最优路径来源于对角线,即 seq_1 和 seq_2 在这个位置匹配。
# 因此,在比对序列 align_1 和 align_2 的过程中,将当前位置的字符添加到两个序列中,并向左上角移动一步。
if route[row][col] == 1:
align_1 += seq_2[row - 1]
align_2 += seq_1[col - 1]
row -= 1
col -= 1