排序第五篇归并排序

news2024/11/24 22:58:33

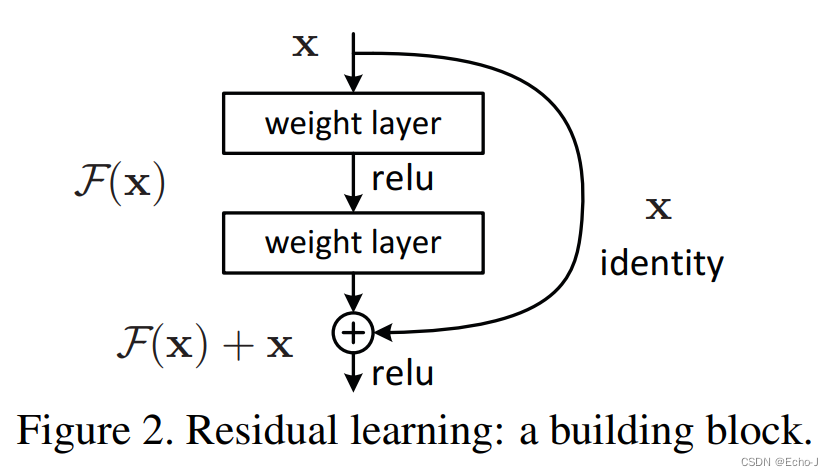
一简介

归并排序(Merge Sort) 的基本思想是：首先将待排序文件看成 $n$ 个长度为1的有序子文件，把这些子文件两两归并，得到 $\frac{n}{2}$ 个长度为 2 的有序子文件；

然后再把这 $\frac{n}{2}$ 个有序的子文件两两归并，如此反复，直到最后得到一个长度为 $n$ 的有序文件为止，这种排序方法称为二路归并排序。

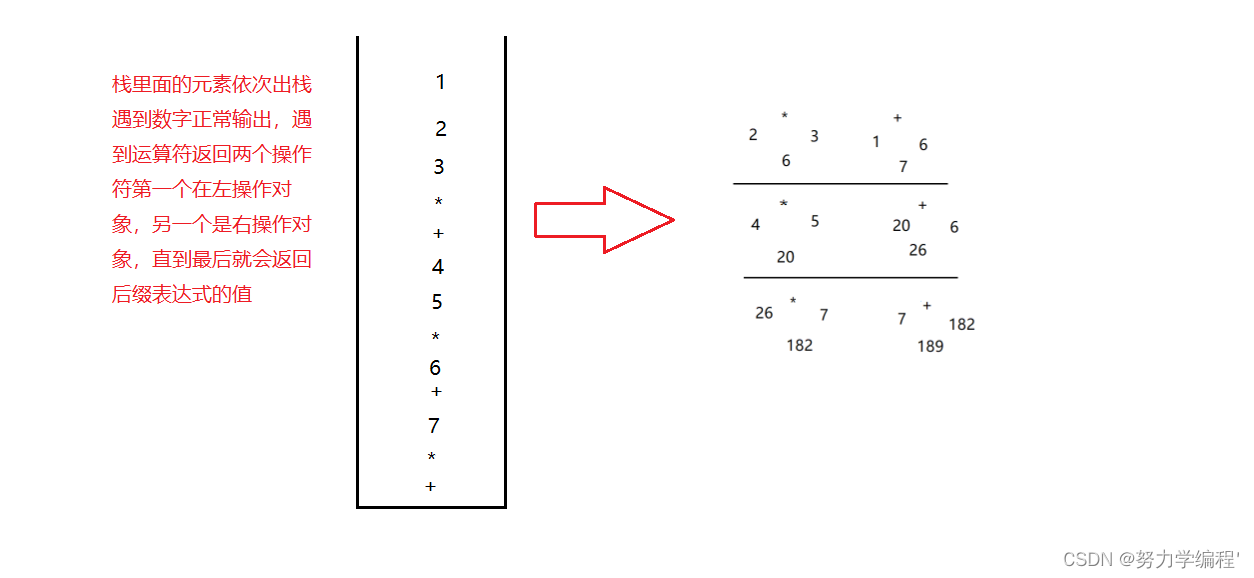
在本文中，我们讨论的归并排序特指二路归并排序. 看一个示意图:
在这里插入图片描述

二实现过程

归并排序的核心操作是将数组中前后相邻的两个有序序列归并为一个有序序列.
以java为例，看一个demo。

public class MergeSort {

    public static void main(String[] args) {
        Integer[] array = new Integer[]{30,45,10,30,50};
        System.out.println("归并排序初始顺序\n"+ Arrays.toString(array));
        mergeSort(array);
        System.out.println("归并排序最后顺序\n"+Arrays.toString(array));
    }

    static void mergeSort(Integer[] arr) {
        sort(arr, 0, arr.length - 1);
    }

    /***
     * 将两个有序序列归并为一个有序序列
     */
    static void sort(Integer[] arr, int low, int high) {
        if (low >= high) {
            return;
        }
        int mid = low + (high - low) / 2;
        sort(arr, low, mid);
        sort(arr, mid + 1, high);
        merge(arr, low, mid, high);
    }

    static void merge(Integer[] arr, int low, int mid, int high) {
        //定义了一个临时数组
        int[] temp = new int[high - low + 1];
        int i = low, j = mid + 1, k = 0;

        while (i <= mid && j <= high) {
            temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
        }
        while (i <= mid) {
            //将原数组从下标 low~middle 中剩余的复制到 temp
            temp[k++] = arr[i++];
        }
        while (j <= high) {
            //将原数组从下标 middle+1 ~ high 中剩余的复制到 temp
            temp[k++] = arr[j++];
        }

        for (i = 0; i < k; i++) {
            arr[low + i] = temp[i];
        }
    }
}

程序运行结果
在这里插入图片描述

归并排序算法

归并排序算法可看作递归算法，虽然有的书写成不是递归算法同样实现了。

三步骤

第一步：一趟归并排序的基本思想是，在某趟归并中，设各子文件长度为len(最后一个子文件的长度可能会小于len), 则归并前 $R [1.. n]$ 共有 $\frac{n}{len}$ 个有序子文件。调用归并操作对子文件进行归并时，必须对子文件的个数可能是奇数、最后一个子文件和长度可能小于 $l e n$ 这两种特殊情况进行处理：

若子文件个数为奇数，则最后个子文件无需和其他子文件归并；
若子文件个数为偶数，则要注意最后一对子文件中后一个子文件的区间上界为 $n$ .

第二步：归并排序的过程需要进行 $log_{2}$ ${n}$ 趟。每一趟排序的操作，就是将两个有序子文件进行归并，
而每一对有序子文件归并时，
记录的比较次数均小于等于记录的移动次数，
记录移动的次数均等于文件中记录的个数，即每一趟归并的时间复杂度为 $O (n)$ 。
因此归并排序的时间复杂度为 $O(nlog_{2}$ $n$ $)$ .
从上述例子可以看出，空间复杂度为 $O (n)$