目录
1 概述
2 蒙特卡洛模拟方法介绍
3 拉格朗日乘子法
4 规模化电动汽车充电负荷预测计算方法
5 Matlab代码实现

1 概述
电动汽车EV(Electric Vehicle)具有清洁环保、高效节能的优点,不仅能缓解化石能源危机,而且能够有效地减少温室气体的排放。2015年10月,国务院发布加快EV充电基础设施建设的指导意见,指出到2020年充电基础设施能满足500万辆EV充电需求,预计未来几年我国EV的保有量将大幅增长。然而,规模化EV的无序充电会加大电网负荷的峰谷差,并对电力系统的规划、配电网的电能质量和经济运行以及稳定性带来显著的影响,反之.对EV的充电行为进行有序优化控制,充分发挥EV作为分布式储能元件的优势,能够实现削峰填谷、平抑可再生能源出力波动的功能,并为电网提供调峰、调频等辅助服务。本文利用蒙特卡洛模拟法和拉格朗日松弛法模拟出电动汽车负荷曲线,同时求解出无序充电功率曲线,作为有序充电曲线的对比基础。
2 蒙特卡洛模拟方法介绍
计算机模拟中的蒙特卡洛法也被称为随机抽样技术或统计检验方法,该方法最重要的特点是它是一种基于概率统计理论的方法。随着科学技术的发展和电子计算机的发明,蒙特卡洛法以其描述物理发展特点和物理实验过程的优点,在各个领域得到了广泛的应用。
在这篇文章有讲解和代码:蒙特卡罗法(随机模拟法)
蒙特卡洛模拟程序结构非常简单,随机数带入公式计算出结果,虽然没有毕竟最优的过程,模拟次数较少时很难得到满意的结果,而蒙特卡罗方法能够真实地模拟实际问题发生过程,故解决问题也比较实际,这也因此在交通运输、机械仿真、物理实验等常见到蒙特卡洛模拟步骤。
蒙特卡洛模拟用法主要是嵌套于仿真模型中,虽然在比赛中不常用,一般在工业生产中,常会遇到拟定几个方案,这时就可以根据不同的模型及规则条件求得结果的分布情况,以评价方案的优劣。
在这篇文章用Matlab实现:整数规划蒙特卡洛模拟(Matlab实现)
3 拉格朗日乘子法
之前在高中就有一直听到拉格朗日,拉格朗日是一个很牛的大佬。在学习SVM的时候,居然也见到了他的身影。让我们了解一下拉格朗日乘子法的具体内容。
在学习过程中,有时会遇到一些最优化问题。这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值(无论最大最小值都可以转化为最小值),二者均是求解最优化问题的方法不同之处在于应用的情形不同。
一般情况下,最优化问题会碰到下面三种:
无约束条件
等式约束条件
不等式约束条件
基本的拉格朗日乘子法就是求函数在约束条件
下的极值的方法。其主要思想是将约束条件函数与原函数联立,从而求出使原函数取得极值的各个变量的解。拉格朗日乘子法是在支持向量机为了更好的求解间距的方法。
在求解最优问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法,在有等式约束时使用拉格朗日乘子法,在有不等式约束的时候使用KTT条件。
这篇文章对拉格朗日乘子法有所总结和应用:
(非线性规划Python)计及动态约束及节能减排环保要求的经济调度
4 规模化电动汽车充电负荷预测计算方法
经过原理及模型研究,假定各用途电动汽车均处于无序充电的状态,具体的计算方法如下:
(1)计算车辆的初始荷电状态和充电所需时长。电动汽车动力电池的剩余电量直接关系到电动汽车的充电所需时间。对于电动汽车的充电所需时间,文章运用电动汽车动力电池的荷电状态( state of charge,SOC)来进行计算。假设电池消耗电量与行驶距离成正比,为已行驶距离,
为电动模式下最大续航里程。此处假定每种不同用途的电动汽车每公里的耗电量相同,最后一次出行结束时的剩余电量由下式计算所得:

式中SOC1为完成充电时的电池荷电状态,SOC2为上一次完成充电时的电池荷电状态。
计算电动汽车充电所需时间T,可以通过将电池容量C、起始荷电状态SOC和充电功率Р求
得,具体公式如下:

(2)计算某一种用途电动汽车在第i个充电负荷计算点时的总充电负荷。本文将每天计算为1440分钟,每15分钟计算一次充电负荷,共计96个充电负荷计算点,计算预测北京市各用途的电动汽车充电负荷,得到各用途电动汽车充电负荷。某一种用途电动汽车的充电负荷的预测计算方法如下:

其中表示第n 台某一种用途电动汽车结束充电的时刻,
表示第n台某种用途电动汽车开始充电的时刻,T表示第n台某种用途电动汽车充电所需时间。某一种用途电动汽车在第 i个充电负荷计算点时的总充电负荷
可由以下方法计算得到

表示第n台电动汽车在第i个充电负荷计算点时的充电负荷,N表示某一种用途电动汽车的保有量。
(3)通过叠加各用途电动汽车的充电负荷得到总的电动汽车充电负荷。第i个充电负荷计算点的总电动汽车充电负荷的计算方式如公式(4-6)所示:

式中,Nc,Nt,Nb分别表示在i时刻充电的电动私家车、电动出租车、电动公交车的数量;,
,
分别表示在i时刻电动私家车、电动出租车、电动公交车的充电负荷大小。
部分代码:
%利用蒙特卡洛模拟法模拟出电动汽车负荷曲线
%同时求解出无序充电功率曲线,作为有序充电曲线的对比基础
clc;clear;
Ntest=100;%仿真程序 车辆数
SOC_end=0.9;
Pbiao=15;%充电功率为15kW
nn=0.9;%充电效率为0.9
Pcharge=Pbiao*nn;%实际充电的功率
Cbattery=30; %电池容量
distance=unifrnd(30,80,1,Ntest); %Ntest辆车 每辆车的单程距离
judge=0.15*distance/Cbattery; %单程耗电SOC
SOC=rand(1,Ntest).*(1-judge)+judge; %初始SOC
......
%解有序充电模型
%分时电价赋值
price=zeros(1,96);
for j=1:33-1
price(j)=0.365;%谷电价0.365元/kWh
end
for j=33:4*8+1-1
price(j)=0.869;%峰电价 元/kWh
end
for j=4*8+1:4*17+1-1
price(j)=0.687;%平电价 元/kWh
end
for j=4*17+1:4*21+1-1
price(j)=0.869;%峰电价 元/kWh
end
for j=4*21+1:4*24+1-1
price(j)=0.687;%平电价 元/kWh
end
deltaT=15/60;%15min折算成小时
cost=0;%购电电价
S=zeros(Ntest,96);
%充电开始时间折算成96点形式
J1=zeros(1,Ntest);
J2=zeros(1,Ntest);
J3=zeros(1,Ntest);
J4=zeros(1,Ntest);
for temp=1:Ntest
J1(temp) =round(4*time1(temp)+1);
J2(temp) =round(4*time2(temp)+1);
J3(temp) =round(4*time3(temp)+1);
J4(temp) =round(4*time4(temp)+1);
end
%是否充电记录数组 1表示充电
yesfirst=zeros(1,Ntest);
yessec=zeros(1,Ntest);
%S(ij)赋初值 也就是无序充电初值
for i=1:Ntest
%到达单位后的充电情况
if(J2(i)-J1(i)~=0)
yesfirst(1,i)=1;
jstart=J1(i);
jend=J2(i);
for temp=jstart:jend
S(i,temp)=1;
end
end
.......
lambda=0.1*ones(1,96);%拉格朗日乘子初值
v=1;
obj=10000000000000000;%初值足够大
jingdu=0.1;
a=1;
b=0.1;
die=100;
while((v<4)&&(die>jingdu))
L=zeros(1,Ntest);
x=zeros(1,96);
SS=zeros(Ntest,96);
%执行智能充电单元
run('ZN.m');
myk=1/(a+b*v);
temp=5087*ones(1,96);
mybsload=bsload(1,1:96);
myh=mybsload+Pcharge*sum(S_yx)-temp;
Tlambda=lambda;
lambda=lambda+myk*myh/norm(myh);
die=norm(lambda-Tlambda,2)/norm(Tlambda);
v=v+1;
end
PSS=zeros(1,97);
PSS(1,1:96)=sum(SS)*Pbiao;
PSS(1,97)=PSS(1,1);
Syouxu=bsload+PSS;
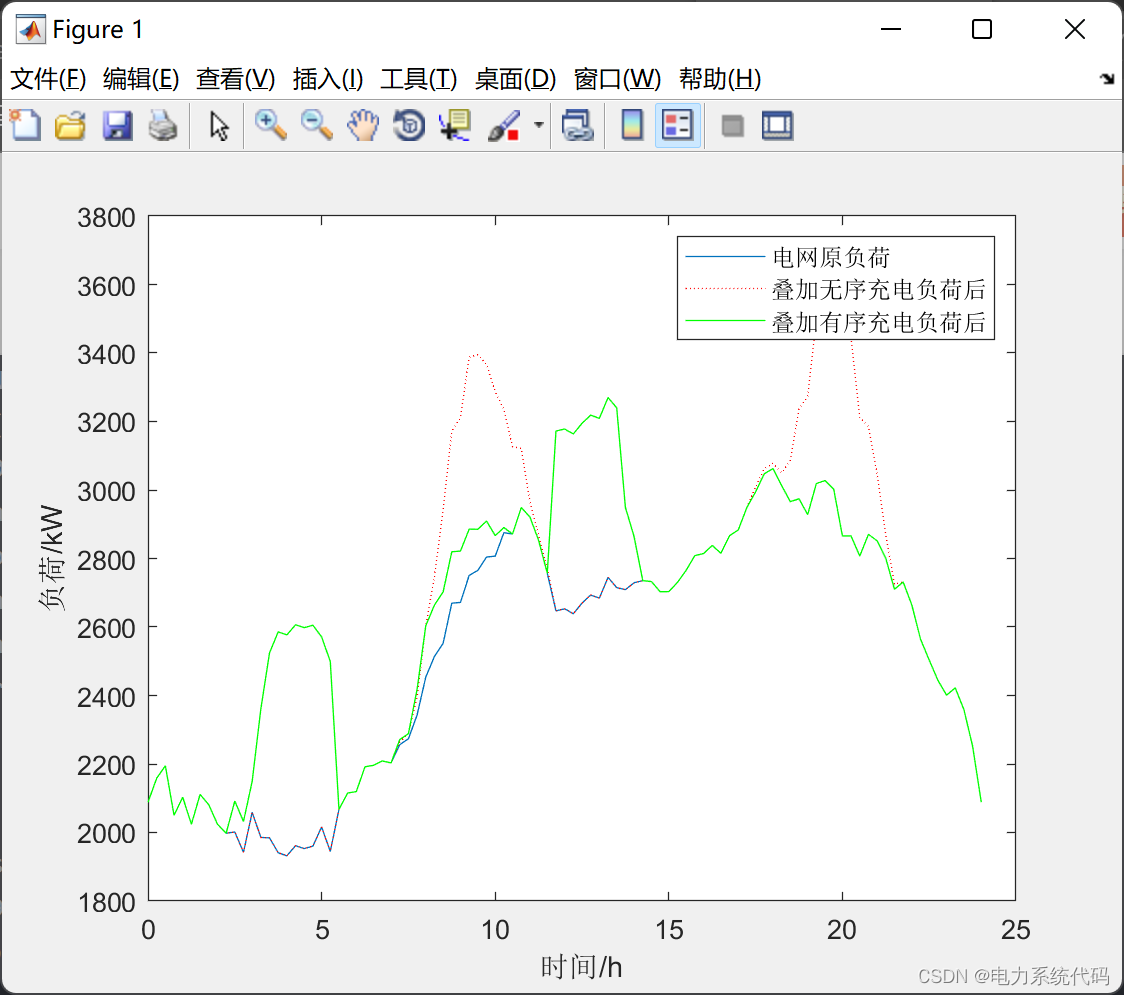
xt=0:0.25:24;
plot(xt,bsload,xt,Swuxu,'r:',xt,Syouxu,'g');
legend('电网原负荷','叠加无序充电负荷后','叠加有序充电负荷后');
xlabel('时间/h');
ylabel('负荷/kW');5 Matlab代码实现