例题——N阶楼梯上楼问题

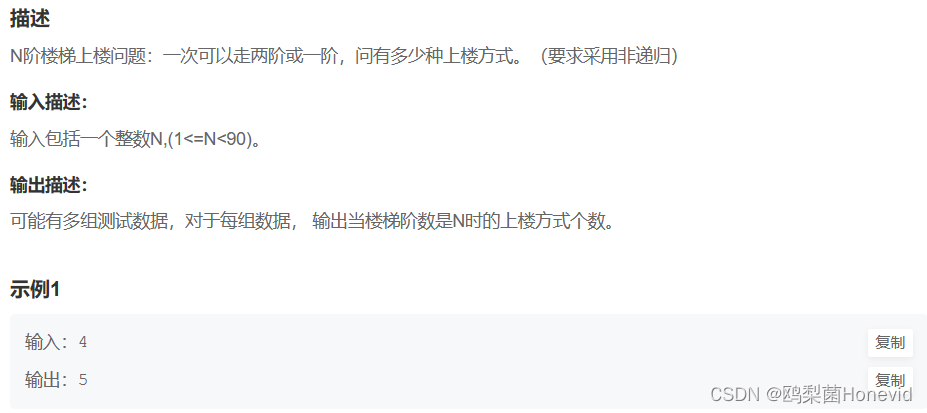
分析

• 大事化小：爬N层有F(N)种可能，有$F(N)=F(N-1)+F(N-2)$
• 小事化了：$F(1)=1，F(2)=2$

递归代码

#include <cstdio>
#include <string>
#include <map>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <climits>
//#include <bits/stdc++.h>
using namespace std;
int variant(int n){
    if (n==1){
        return 1;
    }else if(n==2){
        return  2;
    }
    return variant(n-1)+ variant(n-2);
}

int main() {
    int n;
    while(scanf("%d",&n)!=EOF){
        printf("%d", variant(n));
    }
    return 0;
}

递归的问题

问题：会大量出现重复计算的情况，导致时间复杂度非常高

解决：空间换时间

优化的递归代码

#include <cstdio>
#include <string>
#include <map>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <climits>
//#include <bits/stdc++.h>
using namespace std;

int F[100];
int feibonaci(int n){
    if (F[n]!=-1){
        return F[n];
    }
    if (n==1||n==2){
        F[n] = n;
        return n;
    } else{
        F[n] = feibonaci(n-1)+ feibonaci(n-2);
        return F[n];
    }
}

int main() {
    int n;
    while(scanf("%d",&n)!=EOF){
        for (int i = 0; i < n; ++i) {
            F[i]=-1;
        }
        printf("%d", feibonaci(n));
    }
    return 0;
}

动态规划特点

• 从小问题合并成为大问题

动态规划三要素

1. 状态：定义一个状态描述问题（子问题，小问题：原问题的简化版本）
2. 阶段：子问题的解决方案=================>基于已经解决的问题
3. 决策：如何从一个状态转移到另一个状态=====>不能有回头路，即不能有类似$F(N)=F(N-1)+F(N+1)$出现

动态规划解决问题步骤

1. 利用递归解决问题
2. 寻找重复计算的子问题
3. 设计状态描述这些重复的子问题，通过递推的回归设计阶段变换描述问题转移路径

动态规划代码

#include <cstdio>
#include <string>
#include <map>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <climits>
//#include <bits/stdc++.h>
using namespace std;
int dp[100];
int feibonachi(int n){
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; ++i) {
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n];
}

int main() {
    int n;
    while(scanf("%d",&n)!=EOF){
        printf("%d", feibonachi(n));
    }
    return 0;
}