 167. 木棒 - AcWing题库
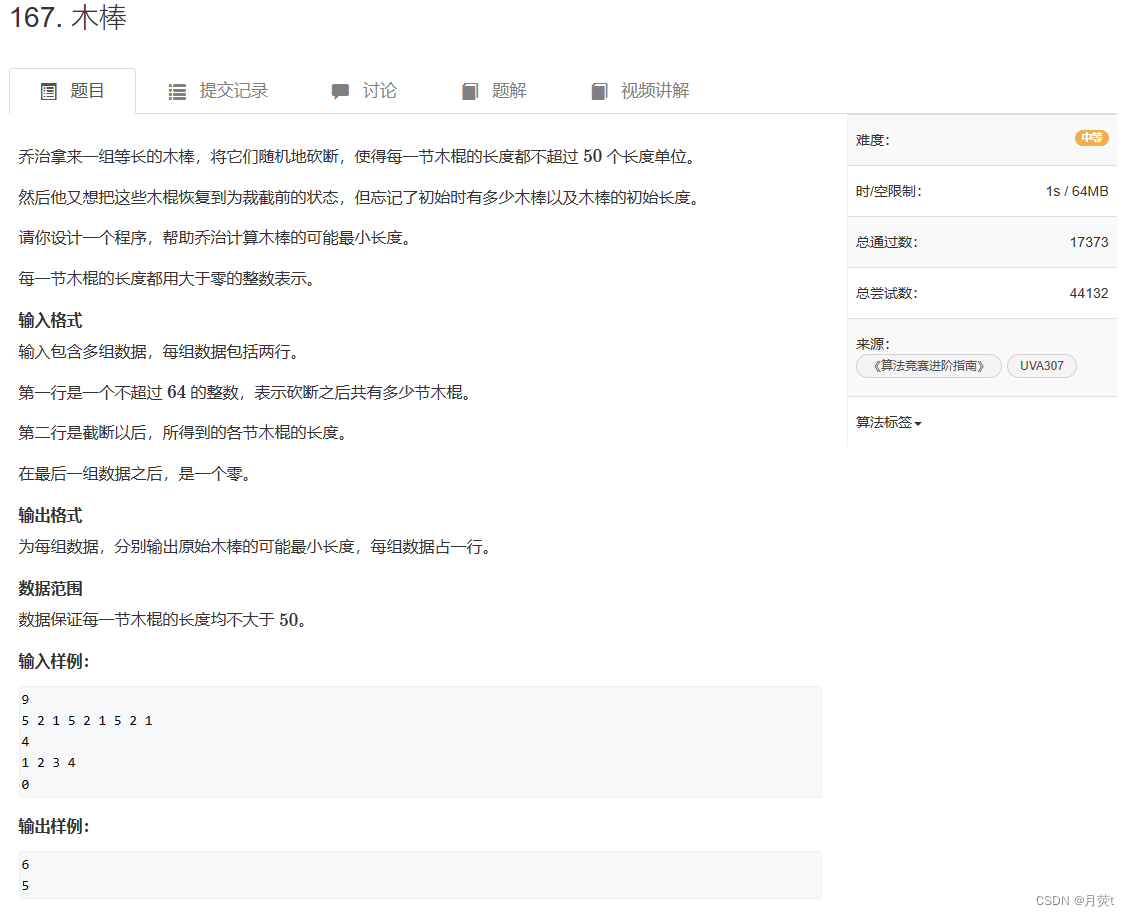
167. 木棒 - AcWing题库
所需知识:dfs,剪枝
思路:首先,将木棍的长度从所有小木棍的最大值开始遍历,遇到的第一个能使所有的小木棍组合成长度相等的大木棍时,则为最优答案,如果想暴力做的话(不考虑剪枝),会超时,所以需要用到剪枝。
剪枝一:因为所有小木棍都要被用来组成大木棍,所以小木棍的总长度一定为大木棍长度的倍数;
剪枝二:将小木棍从大到小排列并组成大木棍使小木棍按顺序排列(以免多种排列,例3 2 1,1 2 3),较大的木棍能占据更大的空间,之后放小木棍的数量就较少一些;遍历的时候直接从小木棍的最大值遍历,因为大木棍不可能由比自己大的木棍组成;
剪枝三:如果一根木棍在第一个位置无解(即此时的len不能使所有小木棍组成n个长度为len的大木棍),则此方案无解;
证明1:
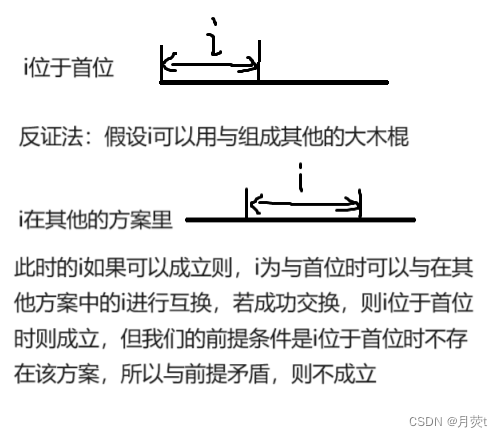
剪枝四:如果一根木棍在最后一个位置无解,则此方案无解;
证明2:与位于首位一样的思路,利用反证法,若最后一个无解,又因为木棍是按照顺序排列的,所以最后一根小木棍,必定放在下一根大木棍的首位,若该方案有解,则两种方案的第i跟木棍可以交换,所以与前提条件矛盾,无解;
剪枝五:若某小木棍放在某位置无解,则与之长度相同的小木棍,也无解,思路同上,利用反证法推导出来矛盾,即可证明该命题不成立;则跳过与i长度相同的木棍;
第一遍看不懂可以多思考几遍,可以自己拿笔在草稿纸上画一画,正所谓“眼看千遍,不如手写一遍”,此题暴力思路并不难,难在剪枝的处理,要将这所有的剪枝一次性想到确实很难,不然很容易TLE;
C++代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 70;
int n,sum,len;
bool st[N];
int w[N];
bool dfs(int x,int l,int t){//x表示当前为第几组木棍,l表示当前木棍的长度,st表示当前木棍的序号
if(x*len==sum) return true;
if(l==len) return dfs(x+1,0,0);
for (int i = t; i <= n; i ++ ){
if(st[i]) continue;//若该木棍被使用过则继续用下一个
if(l+w[i]>len) continue;//若该木棍太长,则继续用下一个
st[i]=true;
if(dfs(x,l+w[i],t+1)) return true;
st[i]=false;
//走到这里的时候dfs(x,l+w[i],t+1)为false,则是无解的时候
if(!l) return false; //若为第一根则直接返回false
if(l+w[i]==len)return false;//若为最后一根根则直接返回false
//若存在与第i根相同的木棍,则直接跳过
int j=i;
while(j<=n&&w[j]==w[i])j++;
i=j-1;
}
return false;
}
int main()
{
while(cin>>n,n){//若输入为0,则停止
//因为有多组数据,要清0
memset(st,0,sizeof st);
sum=0;
len=1;
for (int i = 1; i <= n; i ++ ){
cin>>w[i];
sum+=w[i];
len=max(len,w[i]);
}
sort(w+1,w+1+n);
reverse(w+1,w+1+n);
while(1){
if(sum%len==0&&dfs(0,0,1)){
cout<<len<<endl;
break;
}
len++;
}
}
return 0;
}此题还有注意的事项:
1.输入为0停止
while(cin>>n,n);2.因为有多组数据,每次记得将数据重新初始化:
memset(st,0,sizeof st);
sum=0;
len=1;