相机标定是计算机视觉和机器视觉领域中的一项基本技术,它的主要目的是通过获取相机的内部参数(内参)和外部参数(外参),以及镜头畸变参数,建立起现实世界中的点与相机成像平面上对应像素点之间准确的位置关系。
基本原理
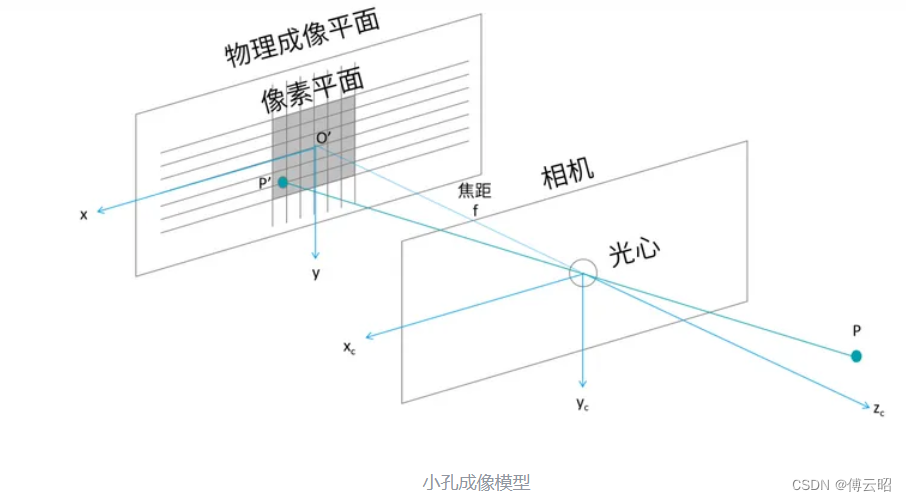
相机标定的基本原理是通过一系列的数学变换和几何模型,将现实世界中的三维坐标点(世界坐标系)转换为相机成像平面上的二维坐标点(图像坐标系)。
坐标系转换
- 世界坐标系:现实世界中的点用三维坐标表示。
- 相机坐标系:以相机光心为原点的三维坐标系。
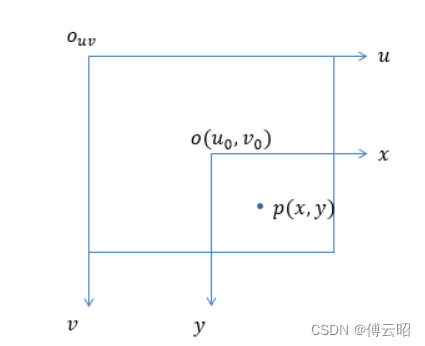
- 成像平面坐标系(图像坐标系):在相机坐标系中,通过成像平面上的点来表示图像中的点。
- 像素坐标系:在成像平面坐标系的基础上,进一步考虑像素的尺寸,以像素为单位。
数学模型
相机标定的数学模型通常基于小孔成像模型。该模型假设光线是直线,且相机内没有畸变。
一个典型的相机标定过程包括以下步骤:
- 建立几何关系:使用一个已知尺寸的标定板(如棋盘格)放置在相机前不同的位置和角度,获取多个视角的图像。
- 特征提取:从每个图像中提取出标定板的角点,这些角点在标定板上的位置是已知的(世界坐标系)。
- 坐标转换:利用相机的内参(焦距、主点等)和外参(相机相对于标定板的位置和方向),以及畸变参数,将世界坐标系中的点转换为像素坐标系中的点。
- 参数估计:通过最小化重投影误差(实际图像点与通过模型计算得到的图像点之间的差异),使用优化算法(如最小二乘法)来求解相机参数。

相机参数
- 内参:焦距(f)、主点(c_x, c_y)、成像平面与相机坐标系之间的比例因子(s)。
- 外参:描述相机在世界坐标系中的位置和方向,由旋转矩阵(R)和平移向量(t)组成。
- 畸变参数:由于镜头制造和安装的原因,实际成像与理想成像存在偏差,这包括径向畸变(k_1, k_2, k_3)和切向畸变(p_1, p_2)。
标定的目的
- 畸变校正:通过校正镜头畸变,生成更接近真实世界的图像。
- 三维重建:在已知相机参数的情况下,可以从多个图像中重构出物体的三维结构。
步骤
1. 准备标定板
- 标定板:通常使用具有明显特征的图案,如黑白相间的棋盘格或圆点图案。
- 尺寸:标定板的实际尺寸需要已知,以便于后续转换计算。
2. 拍摄标定图像
- 使用相机拍摄多张标定板在不同角度和位置的照片。确保标定板在每张照片中至少有一部分是可见的。
3. 特征提取
- 从每个图像中提取标定板的特征点(如棋盘格的角点)。
4. 建立世界坐标系与图像坐标系的关系
- 世界坐标系:假设标定板平面为世界坐标系的XOY平面,标定板上的点可以精确测量。
举例
假设我们有一个10x7的棋盘格,每个格子的大小是1cm x 1cm。
- 世界坐标系:以棋盘格的左上角为原点(0,0,0),每个格子的角点可以按照厘米给出坐标。
5. 相机参数初始化
- 首先需要估计相机参数的初始值,这可以通过一些基本假设来完成,例如假设相机的焦距、主点位于图像中心等。
6. 参数优化
- 使用最小化重投影误差的方法(如张氏标定法、Levenberg-Marquardt算法等)来优化相机参数。
- 重投影误差是指实际观察到的图像点与通过当前相机参数计算得到的图像点之间的差异。
7. 畸变校正
- 一旦获得了相机的内参和畸变参数,就可以对图像进行畸变校正。
举例
- 假设相机由于镜头原因产生了径向畸变,我们可以通过畸变参数来校正图像,使得图像中的直线看起来更加直线。
张氏标定法
张氏标定法(Zhang's Method)是由张正友博士在1998年提出的一种高效且实用的相机标定方法。该方法使用一个平面棋盘格作为标定图案,通过从不同角度拍摄多张图像来标定相机的内参和外参。以下是张氏标定法的基本步骤:
-
准备标定板:使用一个平面棋盘格作为标定图案,棋盘格上的角点坐标是已知的。
-
拍摄标定图像:从不同角度和位置拍摄多张标定板的图像。确保标定板在每张图像中至少有一部分是可见的。
-
提取角点坐标:从每个图像中提取标定板的角点坐标。这些坐标是图像坐标。
-
建立世界坐标系与图像坐标系的关系:假设标定板平面为世界坐标系的XOY平面,标定板上的点可以精确测量。因此,可以建立标定板上的点在世界坐标系和图像坐标系之间的对应关系。
-
初始化相机参数:首先估计相机的内参(焦距、主点等)和外参(相机在世界坐标系中的位置和方向)的初始值。
-
优化相机参数:使用优化算法(如Levenberg-Marquardt算法)最小化重投影误差,即实际观测到的图像点与通过当前相机参数计算得到的图像点之间的差异。通过多次迭代优化,不断调整相机参数,直到重投影误差最小。
-
畸变校正:一旦获得了相机的内参和畸变参数,就可以对图像进行畸变校正。
张氏标定法具有以下优点:
- 高效:只需使用一个平面棋盘格作为标定图案,拍摄多张图像即可。
- 实用:不需要精确知道相机与标定板之间的位姿关系,只需从不同角度拍摄图像即可。
- 精度高:通过优化算法可以精确估计相机的内参和畸变参数。
- 鲁棒性:对于图像质量、光照条件等变化具有较强的鲁棒性。
因此,张氏标定法被广泛应用于相机标定领域,成为计算机视觉和机器人导航等领域的重要技术。
具体步骤详述
a. 特征提取
- 使用OpenCV等计算机视觉库,可以检测出棋盘格的角点。
- 例如,使用OpenCV的
findChessboardCorners()函数。
b. 构建映射关系
- 对于每一张标定图像,提取出的角点在世界坐标系中的位置是已知的。
- 使用相机内参和外参将这些点映射到图像坐标系。
c. 参数优化
- 使用优化算法(如OpenCV中的
calibrateCamera()函数)来计算相机参数。 - 这个过程会最小化所有标定图像上的重投影误差。
d. 畸变校正
- 使用
undistort()函数和计算出的内参、畸变参数来校正图像。
通过以上步骤,我们可以获得一个准确的相机模型,这个模型可以用于后续的视觉任务,如三维重建、机器人导航等。相机标定是一个精确且系统的过程,它要求在标定过程中尽可能减少误差,以确保标定结果的准确性。
为什么至少两张图才能测量内参?
相机内参的测量需要至少两张图的原因在于,单个视角的图像无法提供足够的信息来唯一确定相机的内参。以下是详细解释:
-
单一视角的局限性:单张图像只能提供一个视角下的信息,无法提供关于相机内参的完整信息。例如,无法确定焦距、主点位置等参数。
-
缺乏深度信息:单张图像无法提供深度信息,因为缺乏其他视角的比较。这使得无法准确判断图像中点的真实位置和大小。
-
几何约束不足:为了准确估计内参,需要多个视角下的图像点来建立几何约束。这些约束有助于确定相机内参,如焦距和主点位置。
-
重投影误差最小化:内参的估计通常涉及最小化重投影误差,即实际观测到的图像点与通过内参计算得到的理论图像点之间的差异。这需要多个视角下的图像点来提供足够的数据点。
-
非线性优化:内参的估计通常涉及非线性优化过程,这个过程需要多个数据点来稳定和收敛到全局最小值。
-
畸变参数估计:畸变参数的估计也需要多个视角,因为畸变会随着图像中的位置变化而变化。
因此,为了准确估计相机的内参,通常需要至少两张图像,从不同视角捕捉同一标定板。这些图像提供了多个视角下的信息,有助于建立几何约束,并最小化重投影误差,从而估计出相机的内参。
为什么一般建议拍很多张来进行标定?
在相机内参标定中,一般建议拍摄多张标定板图像,原因如下:
-
提高准确性:更多的图像意味着更多的数据点,这有助于提高内参估计的准确性。每个图像提供了独特的视角,有助于更好地约束内参的估计。
-
减少噪声影响:单张图像可能受到噪声、光照变化等因素的影响。通过拍摄多张图像,可以从多个视角观察标定板,从而平均这些随机误差,提高标定结果的稳定性。
-
增加覆盖范围:多张图像可以提供更全面的覆盖范围,包括标定板的不同部分和不同方向。这有助于捕捉相机的内参在不同条件下的表现。
-
改善优化过程:在最小化重投影误差的优化过程中,更多的数据点有助于算法更好地收敛到全局最优解,并减少陷入局部最优解的风险。
-
畸变估计:畸变参数的估计尤其需要多张图像,因为畸变会随着图像中的位置变化而变化。多张图像可以提供更多关于畸变的分布信息。
-
验证和交叉检验:多张图像可以用来验证和交叉检验标定结果。通过比较不同图像中的标定板点,可以确保内参估计的一致性和准确性。
-
鲁棒性:在实际应用中,相机可能会遇到各种不同的场景和光照条件。拍摄多张图像有助于提高标定结果的鲁棒性,使其在各种条件下都能保持准确性。
因此,为了获得更准确、更稳定的相机内参估计,通常建议拍摄多张标定板图像,最好涵盖不同的视角、位置和光照条件。这样可以确保标定结果在实际应用中的有效性和可
 从棋盘格--》像素坐标,需要左乘相机外参和内参。
从棋盘格--》像素坐标,需要左乘相机外参和内参。
单应性(Homography)变换。可以简单的理解为它用来描述物体在世界坐标系和像素坐标系之间的位置映射关系。对应的变换矩阵称为单应性矩阵。
单应矩阵=相机内参*外参
假设两张图像中的对应点对齐次坐标为(x',y',1)和(x,y,1),单应矩阵H定义为:
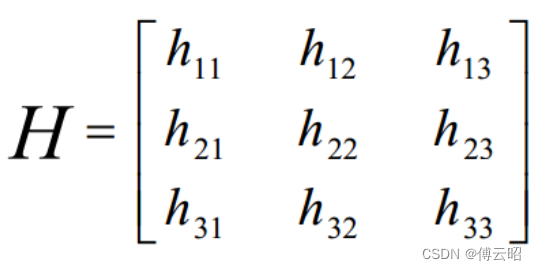
由于单应矩阵H包含了||H||=1约束,因此根据线性方程组,8自由度的H我们至少需要4对对应的点才能计算出单应矩阵。 这也回答了前面图像校正中提到的为何至少需要4个点对的根本原因。
但是,以上只是理论推导,在真实的应用场景中,我们计算的点对中都会包含噪声。比如点的位置偏差几个像素,甚至出现特征点对误匹配的现象,如果只使用4个点对来计算单应矩阵,那会出现很大的误差。因此,为了使得计算更精确,一般都会使用远大于4个点对来计算单应矩阵。另外上述方程组采用直接线性解法通常很难得到最优解,所以实际使用中一般会用其他优化方法,如奇异值分解、Levenberg-Marquarat(LM)算法等进行求解。
因为棋盘标定图纸中所有角点的空间坐标是已知的,这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的,如果我们得到这样的N>=4个匹配点对(越多计算结果越鲁棒),就可以根据LM等优化方法得到其单应矩阵H。
本质上:已经知道多组2D-3D对应点的关系,计算单应矩阵H解从而获取相机内参K,通过最小化重投影误差来获取相机最佳内参。当最后迭代出一个内参K后,不同的2D-3D对应点的重投影误差是不一样的,去掉大的,保留小的,然后继续拍照,重复循环。
参考:
张正友标定法-完整学习笔记-从原理到实战 - 知乎 (zhihu.com)