通过测向交叉定位的方法,按理只需2根测向线即可得出定位点的位置。但由于误差的存在,求出的定位点位置存在一定的偏差。为了得到更加精确的定位点位置,需要对定位点进行冗余测量,从而得到多个定位点,然后通过定位点估计算法得到更加接近真实定位点的位置。
一、基于DBSCAN密度聚类滤除异常定位点
输入参数:
TargetPoint:测量定位点的集合,单位km;
epsilon:ε邻域的半径,单位km;
minPts:最小点数,用于判为同一类的最少点数量;
输出参数:
idx:TargetPoint数组中,属于同一类的索引标志。值为1说明是同一类。
TargetPoint_Cluster:筛选后属于同一类的定位点集合。
%% 对定位点进行聚类,DBSCAN密度聚类
% 定义参数
epsilon = 15; % ε邻域的半径,单位与定位点的坐标单位相同
minPts = 20; % 最小点数,判为同一类的最小点数量
% 进行DBSCAN聚类
idx= DBSCAN(TargetPoint,epsilon,minPts);%TargetPoint为需要进行聚类筛选的所有定位点位置坐标,idx为同一类标志
TargetPoint_Cluster=TargetPoint((idx~=0),:);%筛选聚类后的结果
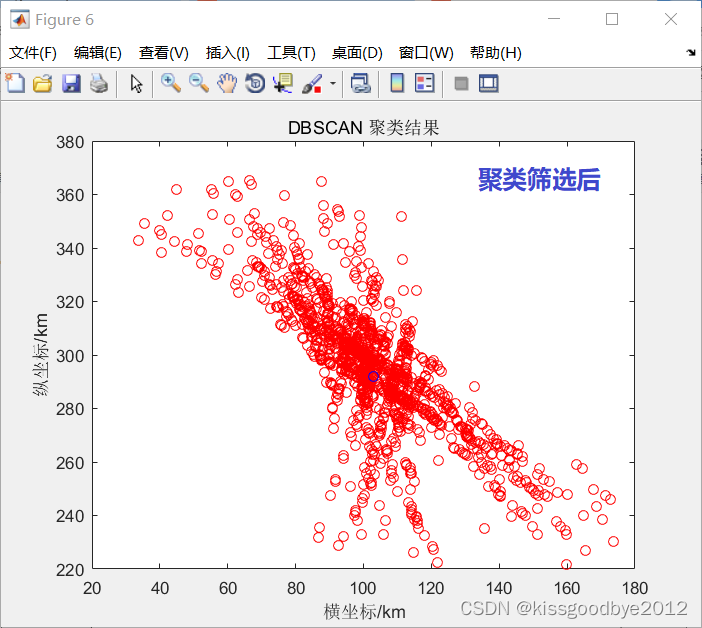
% 可视化聚类结果
figure(6)
plot(TargetPoint_Cluster(:,2),TargetPoint_Cluster(:,1),'ro');
title('DBSCAN 聚类结果');
xlabel('横坐标/km');
ylabel('纵坐标/km');1.1 DBSCAN密度聚类算法Matlab程序
输入参数:
X:测量定位点的集合,单位km;
epsilon:ε邻域的半径,单位km;
minPts:最小点数,用于判为同一类的最少点数量;
输出参数:
idx:X数组中,属于同一类的索引标志。值为1说明是同一类。
isnoise:X数组中,属于噪声点的索引标志。值为1说明是噪声类。
function [IDX, isnoise]=DBSCAN(X,epsilon,MinPts) % DBSCAN聚类函数
C=0; % 统计簇类个数,初始化为0
n=size(X,1); % 把矩阵X的行数数赋值给n,即一共有n个点
IDX=zeros(n,1); % 定义一个n行1列的矩阵
D=pdist2(X,X); % 计算(X,X)的行的距离
visited=false(n,1); % 创建一维的标记数组,全部初始化为false,代表还未被访问
isnoise=false(n,1); % 创建一维的异常点数组,全部初始化为false,代表该点不是异常点
for i=1:n % 遍历1~n个所有的点
if ~visited(i) % 未被访问,则执行下列代码
visited(i)=true; % 标记为true,已经访问
Neighbors=RegionQuery(i); % 查询周围点中距离小于等于epsilon的个数
if numel(Neighbors)<MinPts % 如果小于MinPts
% X(i,:) is NOISE
isnoise(i)=true; % 该点是异常点
else % 如果大于MinPts,且距离大于epsilon
C=C+1; % 该点又是新的簇类中心点,簇类个数+1
ExpandCluster(i,Neighbors,C); % 如果是新的簇类中心,执行下面的函数
end
end
end % 循环完n个点,跳出循环
function ExpandCluster(i,Neighbors,C) % 判断该点周围的点是否直接密度可达
IDX(i)=C; % 将第i个C簇类记录到IDX(i)中
k = 1;
while true % 一直循环
j = Neighbors(k); % 找到距离小于epsilon的第一个直接密度可达点
if ~visited(j) % 如果没有被访问
visited(j)=true; % 标记为已访问
Neighbors2=RegionQuery(j); % 查询周围点中距离小于epsilon的个数
if numel(Neighbors2)>=MinPts % 如果周围点的个数大于等于Minpts,代表该点直接密度可达
Neighbors=[Neighbors Neighbors2]; %#ok % 将该点包含着同一个簇类当中
end
end % 退出循环
if IDX(j)==0 % 如果还没形成任何簇类
IDX(j)=C; % 将第j个簇类记录到IDX(j)中
end % 退出循坏
k = k + 1; % k+1,继续遍历下一个直接密度可达的点
if k > numel(Neighbors) % 如果已经遍历完所有直接密度可达的点,则退出循环
break;
end
end
end % 退出循环
function Neighbors=RegionQuery(i) % 该函数用来查询周围点中距离小于等于epsilon的个数
Neighbors=find(D(i,:)<=epsilon);
end
end1.2 效果展示
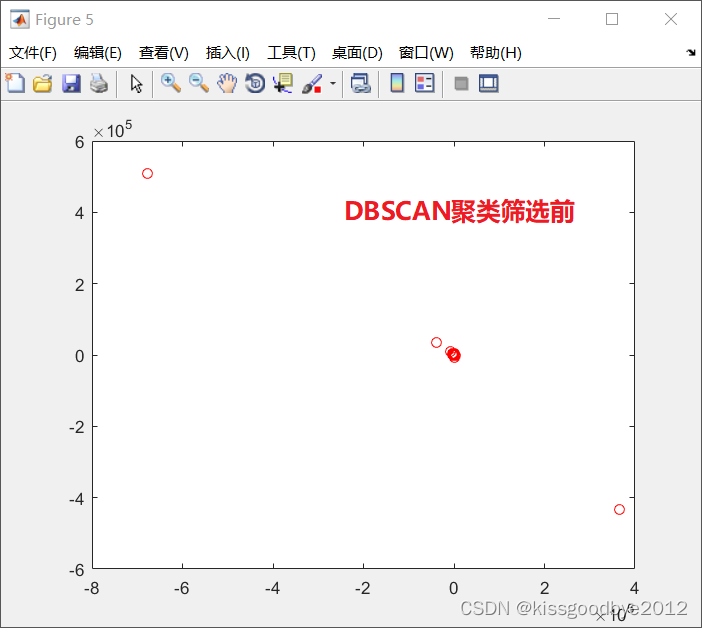
二、最小二乘法求定位点估计值
2.1 算法原理
第一步:由测向原理出发,化简为矩阵形式
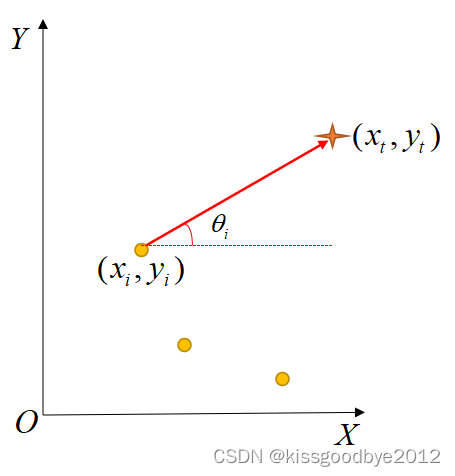
测向线从测量节点指向目标定位点,如图所示,则由直角坐标系下直线的倾斜角定义可得:
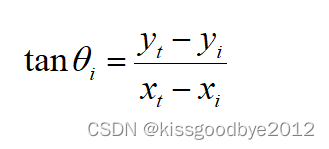
将其化简为AX=B的矩阵形式,如下:
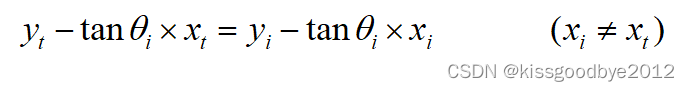
其中,A、X和B矩阵如下所示:
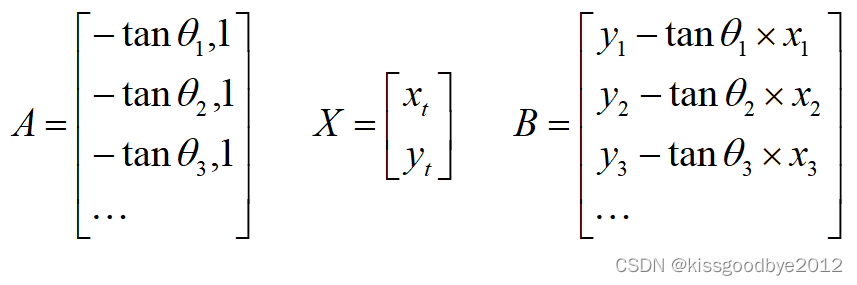
第二步:引入误差项并用最小二乘法求解
由于测向存在误差,因此代入各测量节点坐标和测向值时,上式不能成立。由此引入误差矩阵E(矩阵维度:与矩阵B相同),则上面的矩阵表达式更正为:
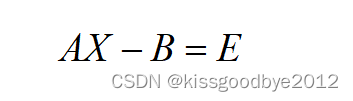
最小二乘法原理:认为该误差的平方和最小时的定位点,为最佳的定位点估计。
该误差的平方和为误差矩阵E的二范数的平方,则
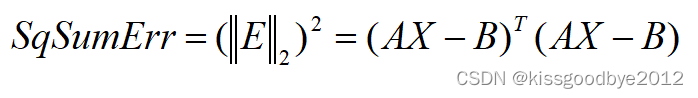
为求得误差平方和的最小值,对其求导数,导数为0时的X即为最佳的定位点估计。

则导数为0时的X为:
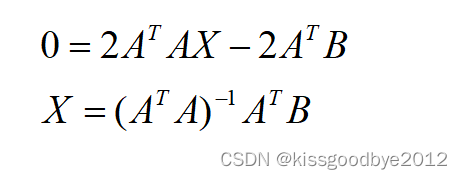
矩阵求导的部分运算法则如下:
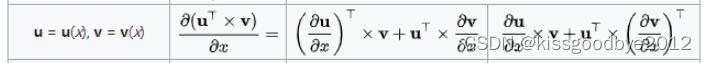
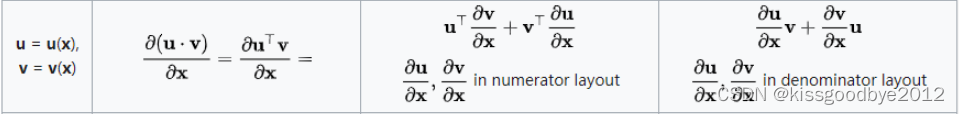
矩阵转置运算法则如下:

2.2 最小二乘法Matlab代码
输入参数:
AOA:测向线对应的地理正北方位,单位度;
R:测量节点的坐标,单位自定;
输出参数:
LocFinalPoint:估计的定位点位置坐标,单位与R保持一致。
%% 最小二乘法求最终定位点
for i=1:size(AOA,2)
A(i,:)=[-tand(Azimuth2ElevationAngle(AOA(i))),1];%倾斜角
B(i)=R(i,2)-tand(Azimuth2ElevationAngle(AOA(i)))*R(i,1);
end
LocFinalPoint=inv(A'*A)*(A'*B');%最小二乘计算结果2.3 效果展示
真实坐标点位置:(100,300)
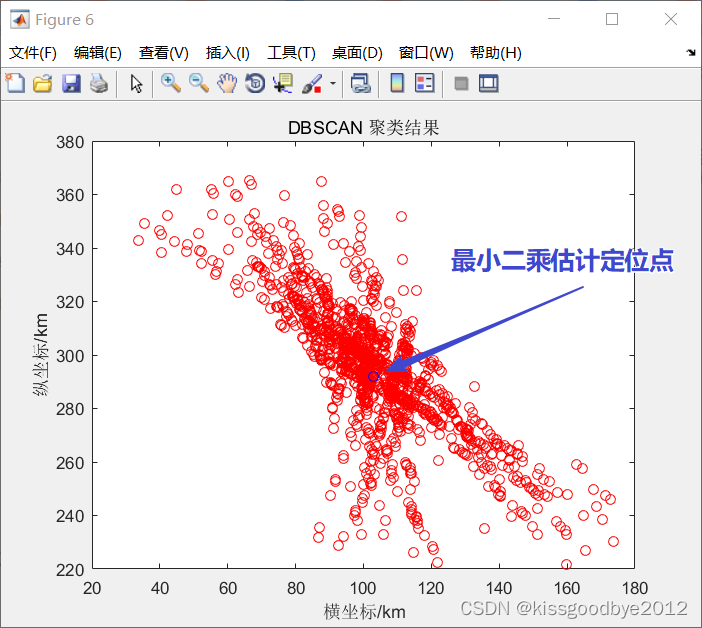
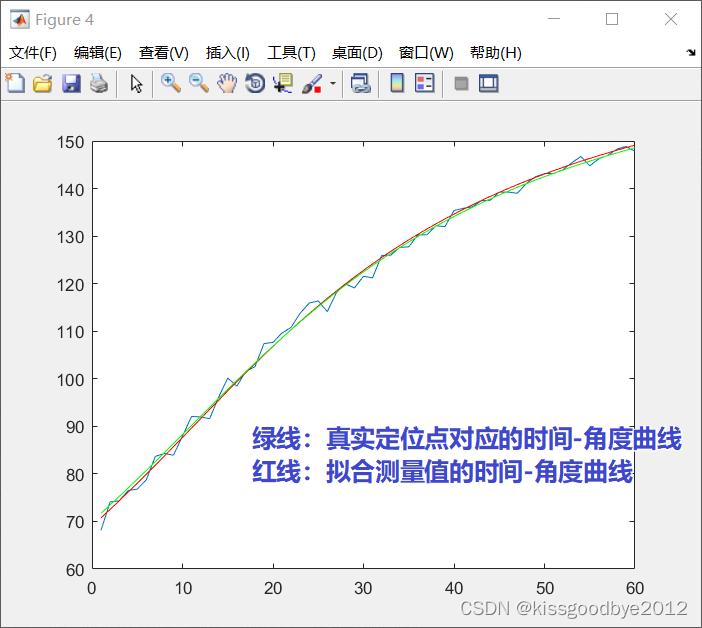
三、利用一元3次方程拟合时间-角度曲线
输入参数:
AOA:测向线对应的地理正北方位,单位度;
输出参数:
yfit:一元3次方程拟合后,对应的地理正北方位,单位度;
%% 三次方程拟合时间-角度曲线后,利用最小二乘法求最终定位点
% 使用polyfit进行线性拟合,1是线性拟合的参数
p = polyfit(1:60,Azimuth2ElevationAngle(AOA), 3);
% 使用polyval计算拟合值
yfit = polyval(p, 1:60);3.1 效果展示
从下图看出,拟合后的时间-角度曲线更加靠近真实定位点对应的时间-角度曲线,使用拟合后的时间-角度曲线,利用最小二乘法估计的定位点坐标更加接近真实定位点。