❀❀❀ 文章由@不准备秃的大伟原创 ❀❀❀
♪♪♪ 若有转载,请联系博主哦~ ♪♪♪
❤❤❤ 致力学好编程的宝藏博主,代码兴国!❤❤❤
halo铁汁们,没错又是你们人见人爱,花见花开的大伟啊,今天也是周六,大伟心情也是非常的美妙啊~ 所以就迫不及待的给大家来更新我们的博客啦,那么今天要学习的内容就是大家早已棋盘不已的二叉树啦,但是在学习二叉树之前,铁汁们有没有把堆认真的学完呢?没有?赶快去看!:堆
OK,那么废话不多说,我们开始今天的学习内容吧!
那么我们上一篇博客也是简单的介绍了一下二叉树的基本概念,那么今天我们就来看一看二叉树的一些操作以及代码的实现。
首先呢,我们先来思考一下一个很重要的问题:我们的二叉树,用什么方法实现好呢?是数组,还是链式结构?
回想一下,我们的堆是不是用数组的方法实现的,但是有一点不知道大家有没有注意到大伟上一篇在介绍堆时说的一句话:“堆的逻辑结构是啥样的?和完全二叉树一个样”,也就是说,我们的完全二叉树也就是用和堆一样的实现方法:数组(这样可以保证数据浪费量很小,大家可以想一想为什么)。
那么问题来了,如果是别的二叉树呢?如果深度比较深,但是最后一层只有一个数据呢?这个时候的空间浪费是不是就是比较大了? 所以,普通的二叉树(当然包括完全二叉树)我们使用链式结构实现就比较银杏。
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,咱们此刻手动快速创建一棵简单的二叉树,快速进入二叉树的操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。 OK不OK?(^▽^ )
铁汁们还记得上一篇博客里面我们提到的二叉树是怎么实现的吗?没错,左孩子右兄弟法,于是我们结构体中就需要一个left指针,一个right指针,还需要一个当前节点的数据data。OK,前提需要已经准备好了,现在,开码!
BT.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树(直接在.c中实现)
BTNode* BTCreate();
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root,int x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);BT.c
手动创建一个二叉树:
BTNode* BTCreate()
{
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
BTNode* n7 = BuyBTNode(7);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
n5->left = n7;
return n1;
} 逻辑结构如下: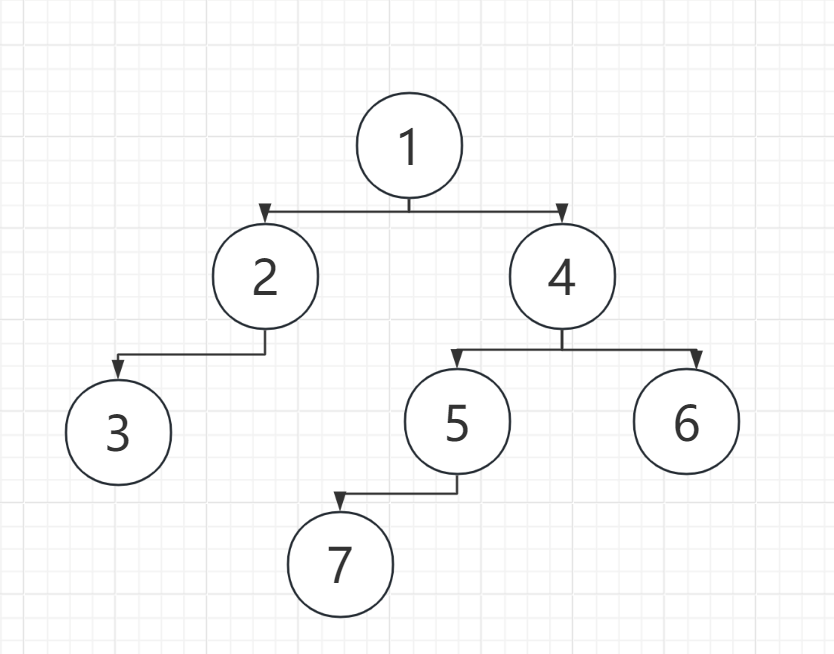
销毁二叉树:
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL) return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
//从根节点开始,递归释放左右节点
free(root);
}二叉树节点个数:
int BinaryTreeSize(BTNode* root)
{
//若根不为空,则递归向下找,每到一个节点加一
return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}二叉树叶子节点个数:
int BinaryTreeLeafSize(BTNode* root)
{
//若根为空
if (root == NULL) return 0;
//若根不为空,但是没有孩子节点,才加一
if (root && root->left == NULL && root->right == NULL) return 1;
//递归向下寻找
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}二叉树第k层节点个数:
int BinaryTreeLevelKSize(BTNode* root, int k)
{
//若当前节点为空,则返回为0
if (root == NULL) return 0;
//若寻找到需要的寻找的层数的某一个节点,则返回1
if (k == 1) return 1;
//从根依次往下找,并且使的k == 1时,就是需要的层数
return BinaryTreeLevelKSize(root->left, --k) + BinaryTreeLevelKSize(root->right, --k);
}
二叉树查找值为x的节点:
BTNode* BinaryTreeFind(BTNode* root,int x)
{
if (root == NULL) return false;
if (root->data == x) return root;
//若需要寻找的值不是根节点,则需要记录一下后面的值为x的节点,以便于返回上一层
BTNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1) return ret1;
BTNode* ret2 = BinaryTreeFind(root->right, x);
if (ret2) return ret2;
return NULL;
}铁汁们肯定还不知道前序遍历是个啥玩意吧,哈哈。那么乘次机会,大伟把前序遍历,中序遍历,后序遍历已经层序遍历都给大家讲一讲:
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
1. 前序遍历 —— 访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历 —— 访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历 —— 访问根结点的操作发生在遍历其左右子树之后。
4. 层序遍历 —— 从根节点开始按照一层一层的访问节点
实例如下图: 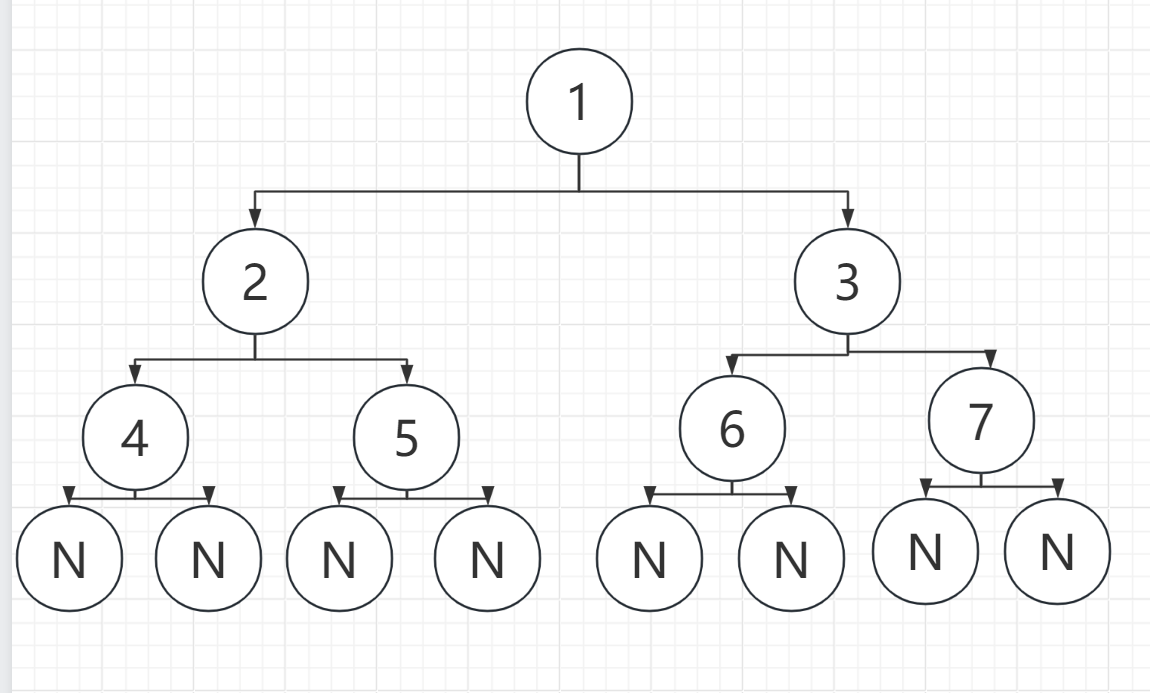
前序遍历是: 1 2 4 N N 5 N N 3 6 N N 7 N N
中序遍历是: N 4 N 2 N 5 N 1 N 6 N 3 N 7 N
后序遍历是: N 7 N 3 N 6 N 1 N 5 N 2 N 4 N
层序遍历是: 1 2 3 4 5 6 7 N N N N N N N N
二叉树前序遍历 :
根据逻辑,我们知道每个最小子树,前序遍历都是 左-根-右的方式遍历的,那接下来我们来看看代码:
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
//先打印当前根节点
printf("%d ", root->data);
//再向下往左找
BinaryTreePrevOrder(root->left);
//再向下往右找
BinaryTreePrevOrder(root->right);
}
二叉树的中序遍历:
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
//先从根节点往左找
BinaryTreeInOrder(root->left);
//等左边最小子树找完了再打印
printf("%d ", root->data);
//再往右找
BinaryTreeInOrder(root->right);
}二叉树的后序遍历:
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
//先从根节点往右找
BinaryTreePostOrder(root->right);
//等右边最小子树找完了再打印
printf("%d ", root->data);
//再找向左找
BinaryTreePostOrder(root->left);
}二叉树的层序遍历:
这个就比较困难了,其实也没有什么很好的方法,不过一般人估计也不会想到,大伟这里就直接给大家答案吧:我们需要借助队列来实现二叉树的层序遍历,那么思路是什么样子的呢?
其实我们实现层序就是要借助队列的性质:后进先出,我们就先把根节点放进队列,然后放根的左节点,再放右节点,将根打印出来后出队列,将队头出队列,将根改为队列的的头,再进当前队头的左右节点,依次循环,直到队列为空。代码简单(这里就不给队列的一系列的操作了,忘记的,或者想去复习复习的铁汁们点这里 :-> 队列)
void LevelOrder(BTNode* root)
{
Queue q;
if (root == NULL)
return;
//队列初始化
QueueInit(&q);
//入队列
QueuePush(&q, root);
//若队列不为空
while (!QueueEmpty(&q))
{
printf("%d\n", QueueFront(&q)->val);
BTNode* a = root->left;
BTNode* b = root->right;
//出队列的头
QueuePop(&q);
//若左不为空
if (a)
QueuePush(&q, a);
//若右不为空
if (b)
QueuePush(&q, b);
//若不为空,则根改为当前队列的头
if (!QueueEmpty(&q))
root = QueueFront(&q);
}
}判断二叉树是不是完全二叉树:
其实我们判断二叉树是不是完全二叉树也有很多办法,但是大伟这里讲一种不是很常见的方法,但是是很容易理解的方法:那就是先假设二叉树是一个完全二叉树,然后通过最后一层所有孩子节点的下标的索引来判断,若有下标索引超过实际二叉树的总节点个数,那么这个二叉树就不是完全二叉树了。代码如下:
bool BinaryTreeComplete(BTNode* root, int index,int n) {
//n为二叉树的总节点个数
// 如果当前节点为空,直接返回 true
if (root == NULL) {
return true;
}
// 如果当前节点的索引超过节点总数,则返回 false
if (index >= n) {
return false;
}
// 递归检查左子树和右子树
return BinaryTreeComplete(root->left, 2 * index + 1,n) &&
BinaryTreeComplete(root->right, 2 * index + 2,n);
}OK,到这里我们所有的二叉树的基本操作就写完了,那么接下来,来玩玩?
test.c
int main()
{
BTNode* root = BTCreate();
//总节点个数
int n = BinaryTreeSize(root);
printf("%d\n", n)
//前序
BinaryTreePrevOrder(root);
printf("\n");
//中序
BinaryTreeInOrder(root);
printf("\n");
//后序
BinaryTreePostOrder(root);
printf("\n");
if (BinaryTreeComplete(root, 0,n))
printf("是完全二叉树");
else
printf("不是完全二叉树");
return 0;
} 我们来看一看结果: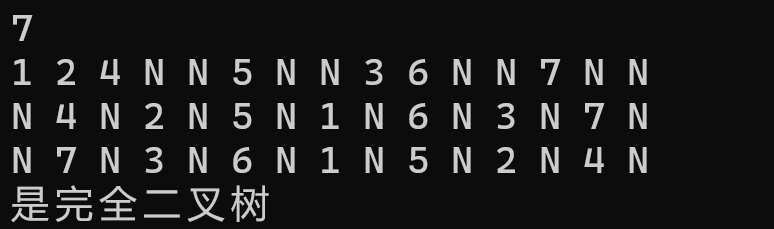
是不是和我们想的一模一样呢~ <(* ̄▽ ̄*)/
其实大伟对递归部分的讲解不是十分详细,但是也是希望铁汁们能好好理解,其实我们学到这里最重要的还是代码的练习量,所以当铁汁们没事做的时候,多刷刷题,多理解理解,O不O K?
到这里本篇博客已经可以是完结了,接着二叉树后面就是排序了,在紧接着就进入c++啦,下篇文章我会对大家介绍数据结构初阶的最后一个内容,请大家继续支持大伟,谢啦!!☆⌒(*^-゜)v
·你要做一个不动声色的大人了。不准情绪化,不准偷偷想念,不准回头看。去过自己另外的生活。你要听话,不是所有的鱼都会生活在同一片海里。---村上春树
本篇博客也就到此为止了,送大家一碗鸡汤,勉励自己以及这世界上所有追逐梦想的赤子趁年华尚好努力提升自己,莫欺少年穷!