1 基本概念

相关性，是指两个变量或者两个系列变量的关联程度，也就是，其中一方变量的变化会影响另外一方变量的变化。

相关性分为三种关系，正相关、负相关以及不相关。

正相关，从单调递增的角度看，其中一方变量的最大值对应另外一方变量的最大值。

负相关，从单调递增的角度看，其中一方变量的最大值对应另外一方变量的最小值。

不相关，不管从任何角度看，其中一方变量与另外一方变量没有关系，也就是，双方变量的变化都不会相互影响。

相关系数，用于度量两个变量或者两个不同系列变量之间的相关程度的数值，简单的相关系数的计算公式的定义如下所示：

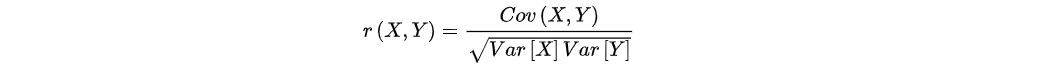
如上所示，r表示X与Y之间的相关系数，r的绝对小于或者等于1，其中，Cov(X,Y)是协方差，Var[X]是X的方差，Var[Y]是Y的方差。r的绝对值越大，则X与Y的相关程度越大，r的绝对值越小，则X与Y的相关程度越小，当r等于0，则X与Y之间不相关。

如上所示，是某企业的广告投入与产出的数据。

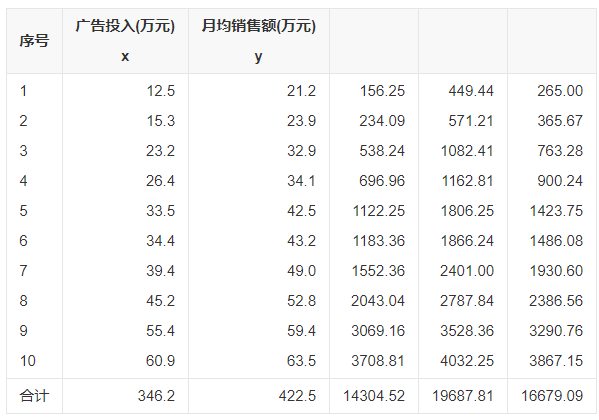
如上所示，计算其相关系数是0.9942，说明广告投入与产出之间发生高度的正相关的关系。

协方差，用于衡量两个变量之间的总体误差，其计算公式的定义如下所示：

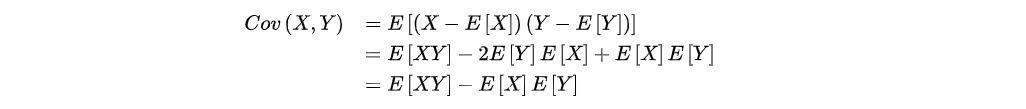
如上所示，E|X|与E|Y|是两个随机变量X与Y的期望值。

方差，用于计算每一个变量与总体均数之间的差异，其计算公式的定义如下所示：

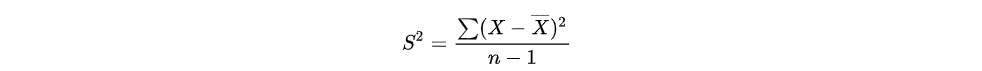
如上所示，S2的平方是样本方差，X为变量，X—为样本均值，n为样本数。

标准差，方差等于标准差的平方，其计算公式的定义如下所示：

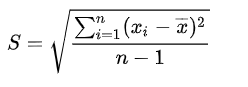
如上所示，标准差的S与方差的S是表示相同的度量。

皮尔森相关系数（Pearson’s correlation），是用于度量两个变量或者两个系列变量X与Y之间的相关性，其计算公式的定义如下所示：

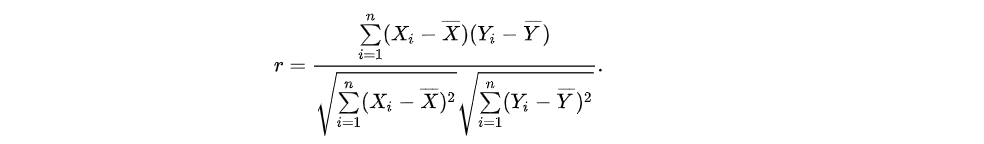
如上所示，Xi与Yi是表示样本X与样本Y，其中，X—与Y—分别表示X与Y的均值。

斯皮尔曼相关系数（Spearman’s correlation），是对样本数据从单调的角度划分为等级，再按照样本数据的等级计算皮尔森相关系数，其计算公式的定义如下所示：

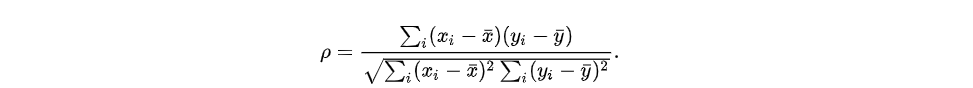
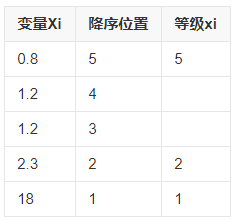
如上所示，其计算公式与皮尔森相关系数的计算公式一样，使用单调的方式按照等级划分样本数据如下所示：

假设检验（Hypothesis testing），该统计分析思想是基于小概率事件作为判断依据，而对提前做出假设的事件H0进行判断，如果小概率事件发生，则假设的事件H0错误，如果小概率的事件不发生，则假设的事件H0正确，因此，小概率事件发生的概率越小，则假设的事件H0越有说服力。

卡方检验（ChiSquareTest），该统计分析思想是统计数据样本的实际观测值与推断值之间的偏离程度，实际观测值与推断值之间的偏离程度决定卡方值的大小，如果卡方值越大，二者的偏差程度就越大，如果卡方值越小，二者的偏差程度就越小，如果二者的值完全相等，则卡方值等于0。

皮尔森卡方检验（Pearson's chi-squared test），该卡方检验是最有名的卡方检验方法之一，而独立性检验是该检验最常用的手段。

独立性检验（X2），根据次数判断两类数据样本是彼此相关的或者是相互独立的，其检验方式的描述是，假设存在两个分类变量X与Y，X对应的列表是{x1,x2}，Y对应的列表是{y1,y2}，则其计算方式如下所示：

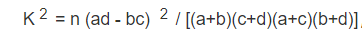
如上所示，计算出随机变量K2 的值，K2 的平方越大，说明X与Y有关系的可能性越大，常用的对照表如下所示：

如上所示，如果K2的值等于6.109，则由以上的对照表可知，5.024≤6.109<6.635，从而，X与Y有关系的概率等于1-0.025等于0.975，即发生的概率是97.5%，因此，X与Y之间有很大可能发生关联关系。

2 基本统计

Apache Spark提供的基本统计包括相关性、假设检验以及汇总，以下章节分别从代码的角度描述这些基本的统计，Spark技术框架目前支持的开发语言包括Python、Java以及R语言。

相关性

相关性的计算是统计学领域中常用的操作，用于分析不同两个变量之间的相关程度。Spark的机器学习技术框架（spark.ml）提供对多系列数据集进行双相关系数的计算，其中包括前面所描述的皮尔森相关系数（Pearson’s correlation）、斯皮尔曼相关系数（Spearman’s correlation）。

如上所示，是Spark技术框架提供Java语言的机器学习的工具集，对输入的数据样本集进行皮尔森相关系数（Pearson’s correlation）、斯皮尔曼相关系数（Spearman’s correlation）的计算。

其中，data是创建了一个4行记录的数据集，每行记录包括4个double类型元素，sparse函数是存储稀疏的列表，稀疏存储方式不存储0值的元素，当列表中的0值元素个数很多的时候，使用稀疏存储方式可以充分利用存储空间，dense函数是存储稠密列表，稠密存储方式存储0值的元素，当列表中的0值元素个数很少的时候，使用稠密存储方式可以提供数据存取的效率。

其中，schema是定义一个数据类型，相当于一个数据库对应的数据表，其字段是features。df是转换成数据框架的形式处理数据集。

其中，Correlation.corr对输入的特征数据集进行相关度的计算，r1输出皮尔森相关系数，r2输出斯皮尔曼相关系数。

假设检验

该统计分析方式在统计学上是一个非常强大的工具，用于检测不同数据样本集合之间是否是显著地发生关联，或者是偶然地发生关联。Spark.ml目前支持皮尔森独立性卡方检测，对每个特征与标签的对应关系进行皮尔森独立性检测，其代码如下所示：

如上所示，data创建一个数据样本集，共计6行数据记录，每行记录包括两列，第一列是标签，第二列是特征集，第二列的每个特征集是包括两个double类型的数值。

其中，schema定义一个类似数据库的数据表格，包括两列，label对应数据样本的第一列标签，featrues对应数据样本的第二列特征集。

其中，df是根据data以及schema创建的数据框架，r是使用spark技术框架计算的卡方检测的结果，该结果中显示每两个输入数据集元组之间发生关联的可能性的统计数据。

汇总分析

数据汇总分析是统计学的一种常用的数据分析方法，spark技术框架提供的汇总分析方法包括列式的最大值（max）、最小值（min）、总和（sum）、方差（variance），标准差（std）、非0值个数、总数个数，其代码如下所示：

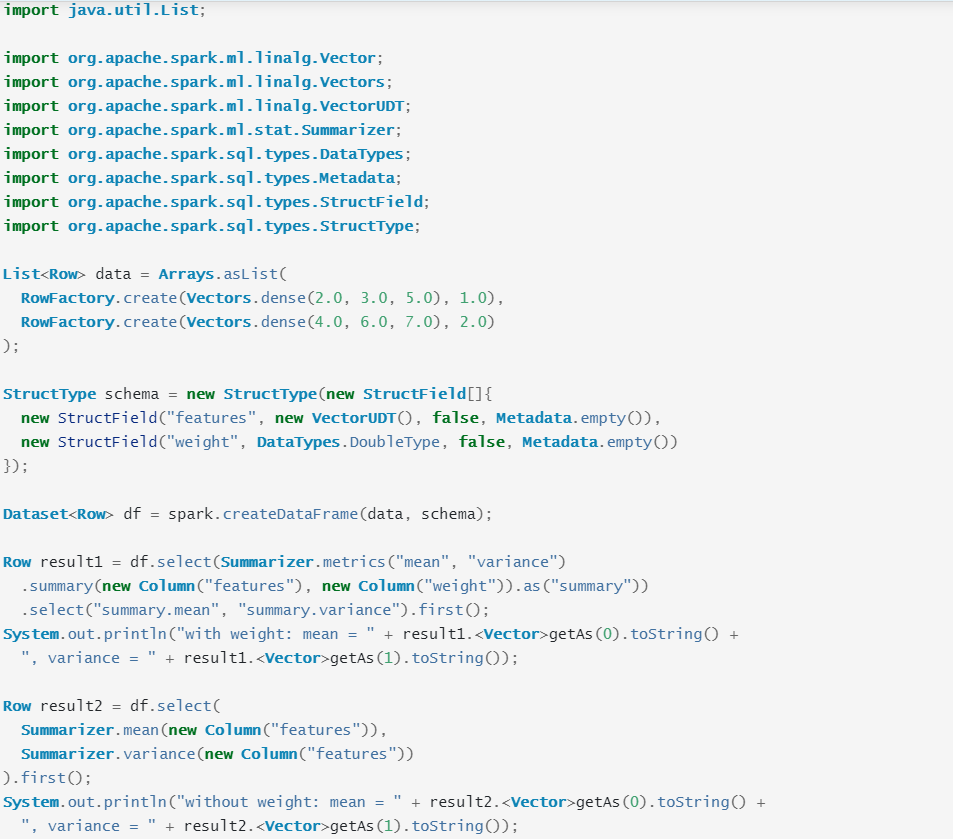
如上所示，data定义一个数据样本集，包括两行记录，每行记录中，第一列表示特征集，第二列表示特征集对应权重值。

其中，schema定义一个类似数据库的数据表格，features表示第一列的特征集，weight表示第二列权重值。

其中，df使用data与schema创建一个数据框架，result1以及result2是计算所得的数据统计分析的结果。

（未完待续）