一、题目描述
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk:
- 每一对相邻的单词只差一个字母。
- 对于 1 <= i <= k 时,每个 si 都在 wordList 中。注意, beginWord 不需要在 wordList 中。
- sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0 。
示例 ——

二、思路
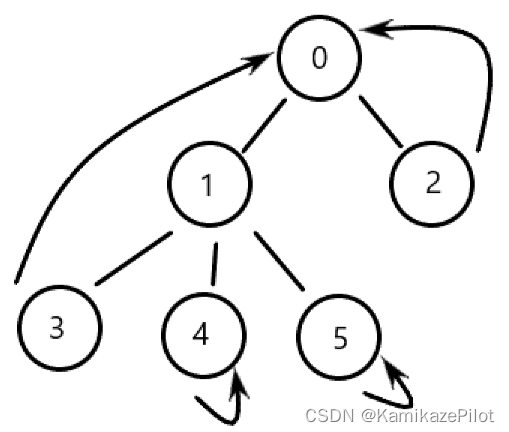
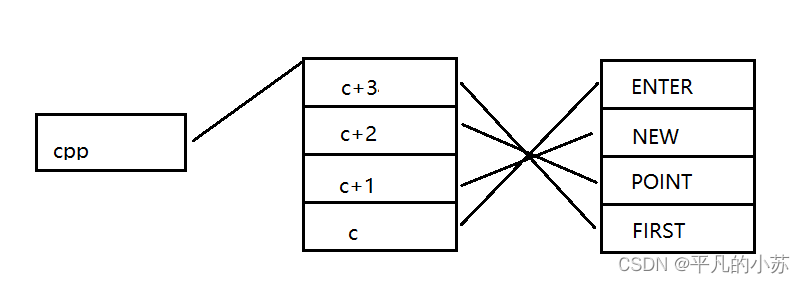
- 最关键的点 : 将单词转化为图中节点,将单词间的关系转化为图的边 —— 只有理解了这个,我们才能理解在本题中对图深搜的使用
- 问题转化:理解了上述后,问题就转化为求图中两个节点间的最近路径长度
- 广度优先搜索 : 我们使用广度优先搜索遍历来求解图中两个节点间的最近路径长度的问题,问题的答案为 —— 搜索到目标节点时,树的深度
对这部分思路的图解如下 :

三、代码
在写代码的过程中,为了使得我们的思路更加清晰,我们需要明确以下几点 :
- 建图
- 提前建立好图,太繁琐,不采用
- 在广度优先搜索过程中,建立图 —— 具体采用的方式为,判断 curWord 只改变一个字母可以转换为那些图中的单词 (该单词要求不能被使用过)
- 广度优先搜索
Queue—— 用于存放搜索过程中树的每一层的节点 (广度优先搜索遍历必用)visit数组 —— 用于记录节点是否被遍历过,对这部分的实现,可以有多种方式。我在实现时,采用set记录遍历过的节点,以判断set中是否存在的形式判断当前节点是否被遍历过。
完整代码:
// 127. 单词接龙
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
if(!wordList.contains(endWord) || wordList.size() == 0){
return 0;
}
int res = 1; // 包括起始点
Queue<String> queue = new LinkedList<>();
queue.offer(beginWord);
Set<String> visit = new HashSet<>(); // 记录是否使用过
visit.add(beginWord);
while (!queue.isEmpty()){
int size = queue.size();
for(int i=0; i<size; i++){ // 遍历当前层
String cur = queue.poll();
if(canChangeTo(queue, cur, endWord, wordList, visit)){ // 构建图
return res+1;
}
}
res++;
}
return 0;
}
// 建立图,找和 cur 相邻的节点
public boolean canChangeTo(Queue<String> queue, String cur, String endWord, List<String> wordList, Set<String> visit){
for(int i=0; i<wordList.size(); i++){ // 遍历所有点
String temp = wordList.get(i);
if(visit.contains(temp)){ // 排除已经用过的点
continue;
}
if(oneLetter(cur, temp)){ // 判断是否相邻
if(temp.equals(endWord)){ // 找到了目标节点,直接返回
return true;
}
queue.offer(temp); // 加入当前层队列
visit.add(temp); // 标记已经使用过
}
}
return false;
}
// 判断 cur 只变化一个单词是否可以得到 temp
public boolean oneLetter(String cur, String temp){
int cnt = 0;
for(int i=0; i<cur.length(); i++){
if(cur.charAt(i) != temp.charAt(i)){
cnt++;
}
if(cnt > 1){
return false;
}
}
return cnt == 1;
}