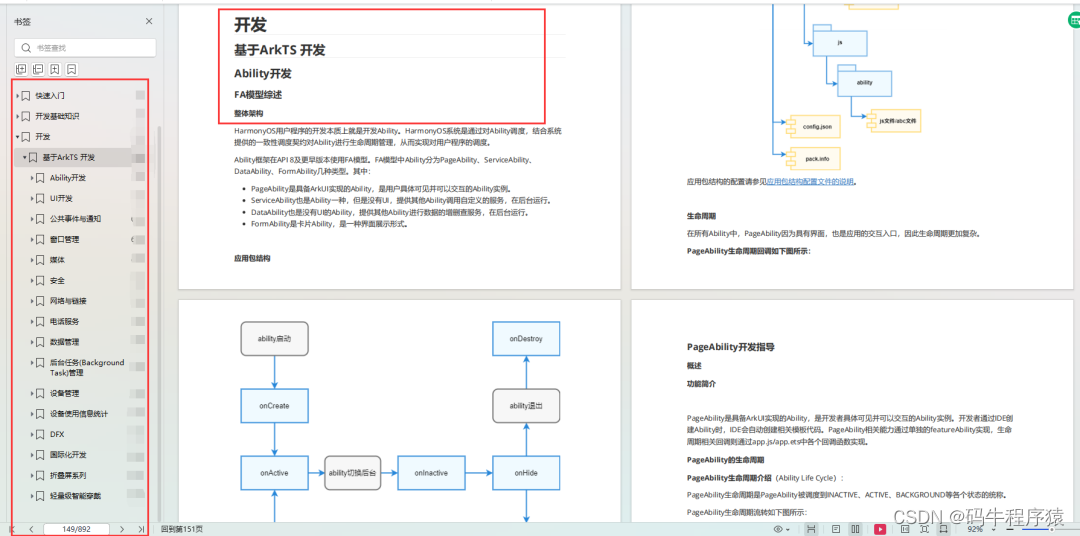
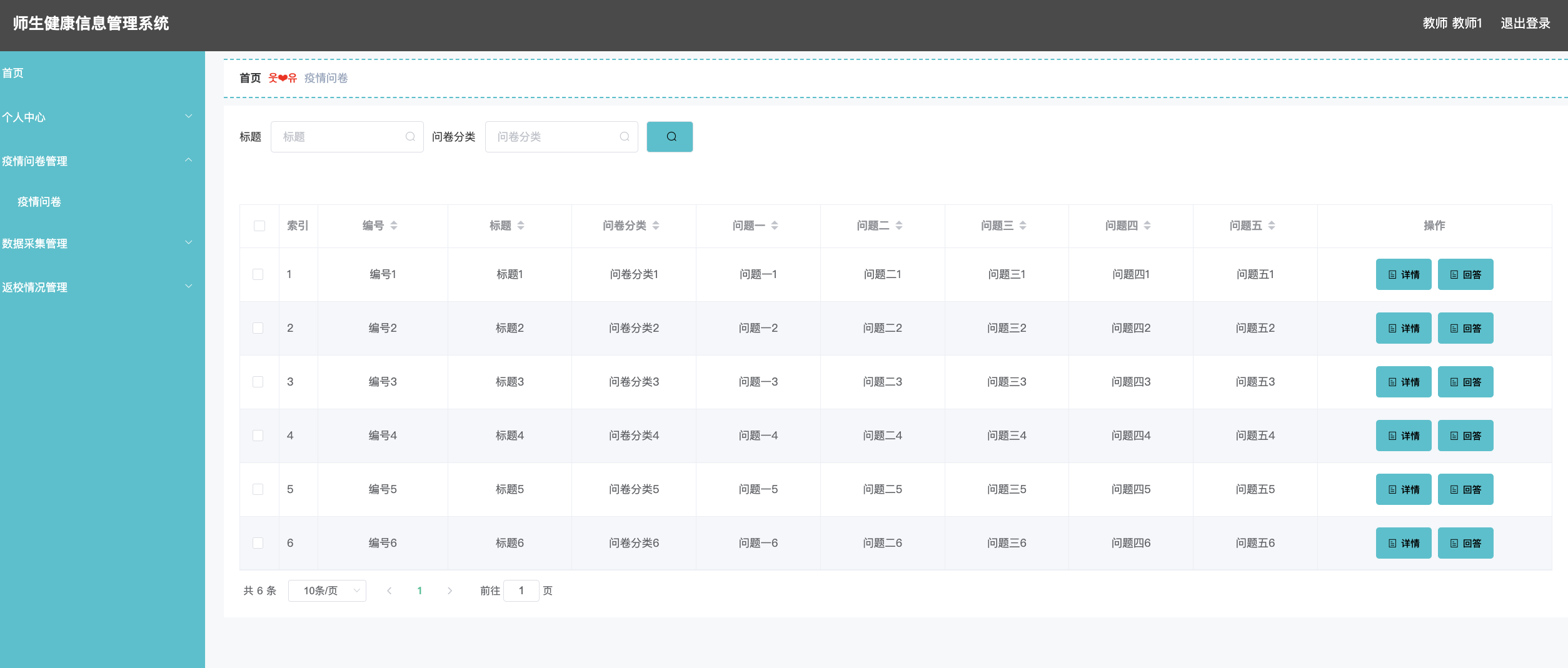
什么是堆
堆(Heap)是计算机科学中一类特殊的数据结构,通常是一个可以被看做一棵完全二叉树的数组对象。
完全二叉树
只有最下面两层节点的度可以小于2,并且最下层的叶节点集中在靠左连续的边界,只允许最后一层有空缺结点且空缺在右边,完全二叉树需保证最后一个节点之前的节点都齐全;
对任一结点,如果其右子树的深度为j,则其左子树的深度必为j或j+1
什么是大顶堆(最大堆)
大顶堆是一种完全二叉树,其每个父节点的值都大于或等于其子节点的值,即根节点的值最大,每个节点的两个子节点顺序没做要求,和之前的二叉查找树不一样。

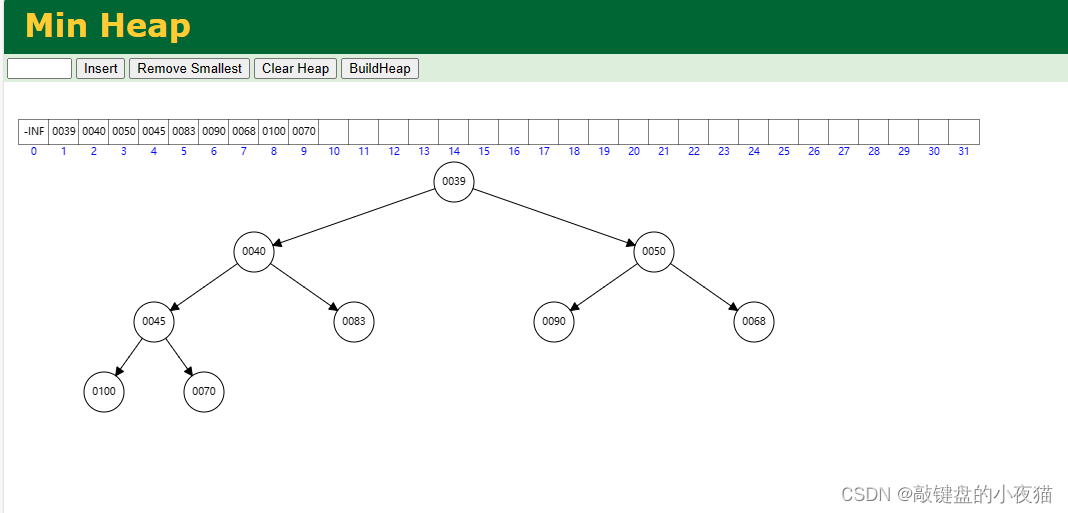
什么是小顶堆(最小堆)
小顶堆是一种完全二叉树,其每个父节点的值都小于或等于其子节点的值,即根节点的值最小。每个节点的两个子节点顺序没做要求,和之前的二叉查找树不一样

存储原理剖析
1)一般升序采用大顶堆,降序采用小顶堆;
2)堆是一种非线性结构,用数组来存储完全二叉树是非常节省空间,把堆看作一个数组
方便操作,一般数组的下标0不存储,直接从1节点存储;
3)堆其实就是利用完全二叉树的结构来维护一个数组;
4)数组中下标为 k 的节点:
左子节点下标为 2*k 的节点;
右子节点就是下标 为 2*k+1 的节点;
父节点就是下标为 k/2 取整的节点;
5)对节点在树中的上下移动
arr[k] 向上移动一层,则让k = k/2
arr[k] 向下移动一层,则让k=2 k 或 k=2 k+1

堆的定义通过公式描述:
大顶堆:arr[k] >= arr[2k+1] && arr[k] >= arr[2k]
小顶堆:arr[k] <= arr[2k+1] && arr[k] <= arr[2k]
应用场景简单介绍
优先级队列、高精度定时器、TopK问题 ...
下面我们将以高精度定时器案例进行讲解和代码实现。
二叉堆构建流程
新插入一个元素之后,就是往数组最后面追加数据,堆可能就不满足堆的特性,需要进行调整,重新满足堆的特点,即该公式:大顶堆:arr[k] >= arr[2k+1] && arr[k] >= arr[2k] ,小顶堆:arr[k] <= arr[2k+1] && arr[k] <= arr[2k],顺着节点所在的路径,向上对比,然后交换。


小顶堆演示动画:Heap Visualization (usfca.edu)
往堆中插入新元素,就是往数组中从索引0或1开始依次存放数据,但是顺序需要满足堆的特性如何让堆满足:
1)不断比较新节点 arr[k]和对应父节点arr[k/2]的大小,根据情况交互元素位置;
2)直到找到的父节点比当前新增节点大则结束;
3)无需关注同级节点;
大顶堆编码实现
大顶堆是一种完全二叉树,其每个父节点的值都大于或等于其子节点的值,即根节点的值最大。
public class Heap {
//用数组存储堆中的元素
private int[] items;
//堆中元素的个数
private int num;
public Heap(int capacity) {
//数组下标0不存储数据,所以容量+1
this.items = new int[capacity + 1];
this.num = 0;
}
/**
* 判断堆中 items[left] 元素是否小于 items[right] 的元素
*/
private boolean rightBig(int left, int right) {
return items[left] < items[right];
}
/**
* 交换堆中的两个元素位置
*/
private void swap(int i, int j) {
int temp = items[i];
items[i] = items[j];
items[j] = temp;
}
/**
* 往堆中插入一个元素,默认是最后面,++num先执行,然后进行上浮判断操作
*/
public void insert(int value) {
items[++num] = value;
up(num);
}
/**
* 使用上浮操作,新增元素后,重新堆化
* 不断比较新节点 arr[k]和对应父节点arr[k/2]的大小,根据情况交互元素位置
* 直到找到的父节点比当前新增节点大则结束
* <p>
* 数组中下标为 k 的节点
* 左子节点下标为 2*k 的节点
* 右子节点就是下标 为 2*k+1 的节点
* 父节点就是下标为 k/2 取整的节点
*/
private void up(int k) {
//父节点 在数组的下标是1,下标大于1都要比较
while (k > 1) {
//比较 父结点 和 当前结点 大小
if (rightBig(k / 2, k)) {
//当前节点大,则和父节点交互位置
swap(k / 2, k);
}
// 往上一层比较,当前节点变为父节点
k = k / 2;
}
}
/**
* 删除堆中最大的元素,返回这个最大元素
*/
public int delMax() {
int max = items[1];
//交换索引 堆顶的元素(数组索引1的)和 最大索引处的元素,放到完全二叉树中最右侧的元素,方便后续变为临时根结点
// 为啥不能直接删除顶部元素,因为删除后会断裂,成为森林,所以需要先交互,再删除
swap(1, num);
//最大索引处的元素删除掉, num--是后执行,元素个数需要减少1
items[num--] = 0;
//通过下浮调整堆,重新堆化
down(1);
return max;
}
/**
* 使用下沉操作,堆顶和最后一个元素交换后,重新堆化
* 不断比较 节点 arr[k]和对应 左节点arr[2*k] 和 右节点arr[2*k+1]的大小,如果当前结点小,则需要交换位置
* 直到找到 最后一个索引节点比较完成 则结束
* <p>
* 数组中下标为 k 的节点
* 左子节点下标为 2*k 的节点
* 右子节点就是下标 为 2*k+1 的节点
* 父节点就是下标为 k/2 取整的节点
*/
private void down(int k) {
//最后一个节点下标是num
while (2 * k <= num) {
//记录当前结点的左右子结点中,较大的结点
int maxIndex;
if (2 * k + 1 <= num) { //2 * k + 1 <= num 是判断 确保有右节点
//比较当前结点下的左右子节点哪个大
if (rightBig(2 * k, 2 * k + 1)) {
maxIndex = 2 * k + 1;
} else {
maxIndex = 2 * k;
}
} else {
maxIndex = 2 * k;
}
//比较当前结点 和 较大结点的值, 如果当前节点较大则结束
if (items[k] > items[maxIndex]) {
break;
} else {
//否则往下一层比较,当前节点k索引 变换为 子节点中较大的值
swap(k, maxIndex);
//变换k的值
k = maxIndex;
}
}
}
// 测试
public static void main(String[] args) {
Heap heap = new Heap(20);
heap.insert(42);
heap.insert(48);
heap.insert(93);
heap.insert(21);
heap.insert(90);
heap.insert(9);
heap.insert(3);
heap.insert(40);
heap.insert(32);
int top;
while ((top = heap.delMax()) != 0) {
System.out.print(top + ",");
}
}
}堆应用案例:高精度定时器
实现一个定时器的任务存储,支持很多不同时间的定时任务,要求高精度,1秒级别执行
方案一:
数据库建立一个task表,存储到数据库或Redis里面,每隔1秒扫描一遍定时任务列表,获取要执行的任务;
缺点:每次都需要遍历整个定时任务列表,有些很久才执行的任务,也需要被IO遍历,浪费CPU,由于列表比较大,每次遍历都耗时多;

方案二:
使用【小顶堆】数据结构存储,小顶堆的插入操作就是在最小堆最后插入一个节点,然后重新调整小顶堆的结构,每隔一秒扫下堆顶元素,删除堆顶元素进行执行任务即可,然后重新堆化
key规则是【年月日时分秒】比如:2024-03-29-23-41-22 作为key,堆顶的元素就是最小的。
优先级队列: 传统队列特性就是先进先出,支持优先级排序,优先级高的最先出队(大顶堆实现),优先级队列实现方式有多种,堆去实现属于高效的一种方案
Java的PriorityQueue就是通过二叉小顶堆实现,用一棵完全二叉树表示,通过数组来作为PriorityQueue的底层实现,JDK的PriorityQueue默认是最小堆,可以使用比较器来让它变成最大堆。
编码实现
public class MaxHeapPriorityQueue<T extends Comparable<T>> {
/**
* 用数组存储堆中的元素
*/
private T[] items;
/**
* 记录堆中的元素个数
*/
private int num;
public MaxHeapPriorityQueue(int capacity) {
//数组下标0,不存储数据,所有容量要+1
this.items = (T[]) new Comparable[capacity+1];
this.num = 0;
}
/**
* 判断队列是否为空
* @return
*/
public boolean isEmpty() {
return num==0;
}
/**
* 比较大小,item[left] 元素是否小于 item[right]的元素
*/
private boolean rightBig(int left, int right) {
return items[left].compareTo(items[right])<0;
}
/**
* 交互堆中两个元素的位置
*/
private void swap(int i, int j) {
T temp = items[i];
items[i] = items[j];
items[j] = temp;
}
/**
* 往堆中插入一个元素,默认是数组最后面,然后进行上浮操作,++num会先执行,第一个数组0索引不存储数据
*/
public void insert(T value) {
items[++num] = value;
up(num);
}
/**
* 使用上浮操作,新增元素后,重新堆化
* 不断比较新节点 arr[k]和对应父节点arr[k/2]的大小,根据情况交互元素位置
* 直到找到的父节点比当前新增节点大则结束
* <p>
* 数组中下标为 k 的节点
* 左子节点下标为 2*k 的节点
* 右子节点就是下标 为 2*k+1 的节点
* 父节点就是下标为 k/2 取整的节点
*/
private void up(int k) {
//父节点,在线数组的下标是1,数组索引大于1都要比较
while (k > 1) {
//比较 父节点 和 当前节点 的大小
if (rightBig(k / 2, k)) {
//如果当前节点比父节点大,则交互位置
swap(k / 2, k);
}
//当前节点往上一层,当前节点变成父节点
k = k / 2;
}
}
/**
* 使用下沉操作,堆顶和最后一个元素交换后,重新堆化
* 不断比较 节点 arr[k]和对应 左节点arr[2*k] 和 右节点arr[2*k+1]的大小,如果当前结点小,则需要交换位置
* 直到找到 最后一个索引节点比较完成 则结束
* <p>
* 数组中下标为 k 的节点
* 左子节点下标为 2*k 的节点
* 右子节点就是下标 为 2*k+1 的节点
* 父节点就是下标为 k/2 取整的节点
*/
private void down(int k) {
// 最后一个节点的下标是num
while (2 * k <= num) {
//记录当前节点的左右子节点,较大的节点
int maxIndex;
if (2 * k + 1 <= num) {
if (rightBig(2 * k, 2 * k + 1)) {
maxIndex = 2 * k + 1;
} else {
maxIndex = 2 * k;
}
} else {
maxIndex = 2 * k;
}
//比较当前节点和较大接的值,如果当前节点大则结束
if (items[k].compareTo(items[maxIndex]) > 0) {
break;
} else {
//否则往下一层比较,当前节点的k变为子节点中较大的值
swap(k, maxIndex);
k = maxIndex;
}
}
}
/**
* 删除堆中最大的元素,并且返回这个元素
*
* @return
*/
public T delMax() {
T maxValue = items[1];
//交换索引 堆顶的元素(数组索引1的)和 最大索引处的元素,放到完全二叉树中最右侧的元素,方便后续变为临时根结点
// 为啥不能直接删除顶部元素,因为删除后会断裂,成为森林,所以需要先交互,再删除
swap(1, num);
//最大索引处的元素删除,num--是后执行,元素个数需要减少1
items[num--] = null;
//通过下沉操作,重新堆化
down(1);
return maxValue;
}
}public class Task implements Comparable<Task> {
private int weight;
private String name;
public Task(String name,int weight){
this.weight = weight;
this.name = name;
}
public void doTask(){
System.out.println(name+" task 运行,权重 = "+weight);
}
@Override
public int compareTo(Task task) {
return this.weight - task.weight;
}
} public static void main(String[] args) {
MaxHeapPriorityQueue<Task> queue = new MaxHeapPriorityQueue(20);
queue.insert(new Task("99任务",99));
queue.insert(new Task("88任务",88));
queue.insert(new Task("200任务",200));
queue.insert(new Task("70任务",70));
queue.insert(new Task("300任务",300));
queue.insert(new Task("10任务",10));
//通过循环从队列中获取最大的元素
while(!queue.isEmpty()){
Task task = queue.poll();
task.doTask();
}
}