递归方法调用
:方法自己调用自己的现象就称为递归。
递归的分类
:
直接递归、间接递归。
直接递归:方法自身调用自己
public void methodA (){methodA ();}
间接递归:可以理解为A()方法调用B()方法,B()方法调用C()方法,C()方法调用A()方法。
public static void A (){B ();}public static void B (){C ();}public static void C (){A ();}
说明
:
递归方法包含了一种
隐式的循环
。
递归方法会
重复执行
某段代码,但这种重复执行无须循环控制。
递归一定要向
已知方向
递归,否则这种递归就变成了无穷递归,停不下来,类似于
死循环
。最终
发生
栈内存溢出
。
举例1:计算1 ~ n的和
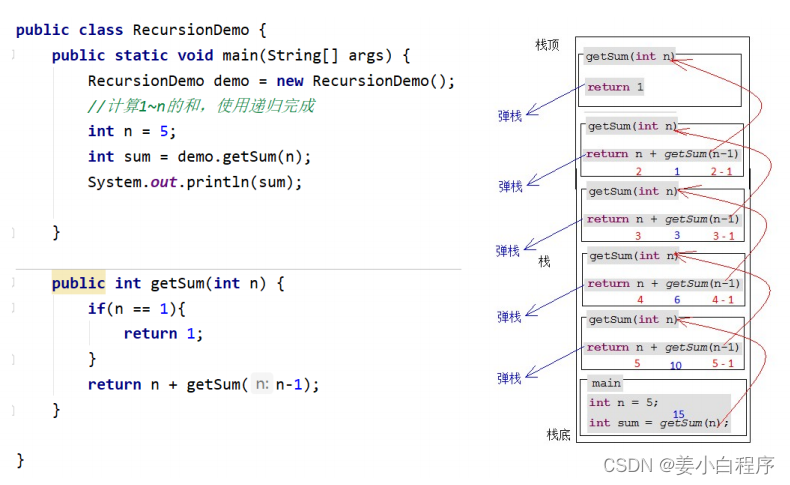
public class RecursionDemo {public static void main ( String [] args ) {RecursionDemo demo = new RecursionDemo ();// 计算 1~num 的和,使用递归完成int num = 5 ;// 调用求和的方法int sum = demo . getSum ( num );// 输出结果System . out . println ( sum );}/*通过递归算法实现 .参数列表 :int返回值类型 : int*/public int getSum ( int num ) {/*num 为 1 时 , 方法返回 1,相当于是方法的出口 ,num 总有是 1 的情况*/if ( num == 1 ){return 1 ;}/*num 不为 1 时 , 方法返回 num +(num-1) 的累和递归调用 getSum 方法*/return num + getSum ( num - 1 );}}
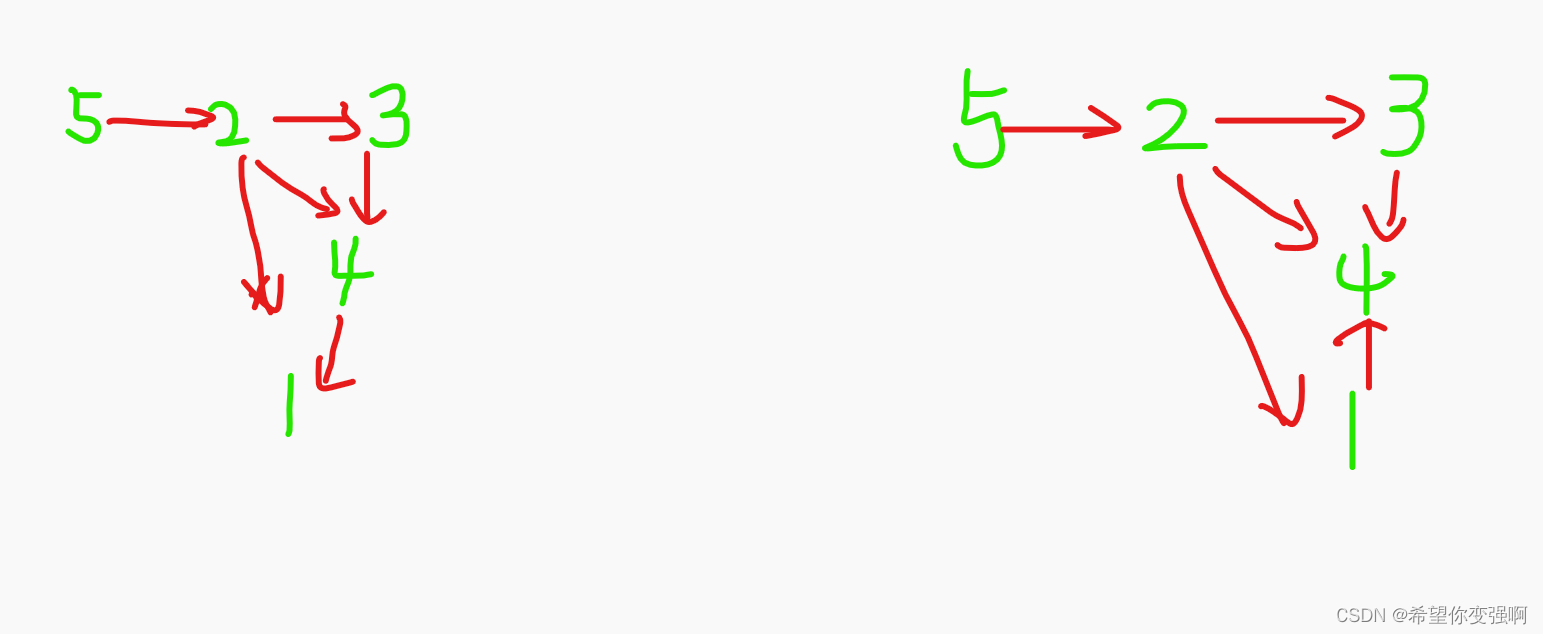
代码执行图解:
代码解释
/* * 当程序执行时,它会按照以下流程进行: 1. `main` 方法被调用。 2. 一个 `RecursionDemo` 类的对象 `demo` 被创建。 3. `n` 被赋值为 5。 4. 调用 `demo.getSum(n)` 方法,其中 `n` 的值为 5。 5. 进入 `getSum` 方法。 6. `n` 的值不为 1,因此程序执行 `return n + getSum(n - 1);`,其中 `n - 1` 的值为 4。 7. 程序递归调用 `getSum` 方法,将参数值 `4` 传递给它。 8. 再次进入 `getSum` 方法。 9. `n` 的值不为 1,因此程序执行 `return n + getSum(n - 1);`,其中 `n - 1` 的值为 3。 10. 程序递归调用 `getSum` 方法,将参数值 `3` 传递给它。 11. 再次进入 `getSum` 方法。 12. `n` 的值不为 1,因此程序执行 `return n + getSum(n - 1);`,其中 `n - 1` 的值为 2。 13. 程序递归调用 `getSum` 方法,将参数值 `2` 传递给它。 14. 再次进入 `getSum` 方法。 15. `n` 的值不为 1,因此程序执行 `return n + getSum(n - 1);`,其中 `n - 1` 的值为 1。 16. 程序递归调用 `getSum` 方法,将参数值 `1` 传递给它。 17. 再次进入 `getSum` 方法。 18. `n` 的值为 1,因此程序直接返回 1。 19. 回到上一层递归调用,将返回的值 1 加上当前层的 `n` 的值(为 2),得到结果 3,返回给上一层。 20. 继续返回上一层递归调用,将返回的值 3 加上当前层的 `n` 的值(为 3),得到结果 6,返回给上一层。 21. 继续返回上一层递归调用,将返回的值 6 加上当前层的 `n` 的值(为 4),得到结果 10,返回给上一层。 22. 继续返回上一层递归调用,将返回的值 10 加上当前层的 `n` 的值(为 5),得到结果 15,返回给上一层。 23. 回到 `main` 方法,将返回的结果 15 赋值给 `sum` 变量。 24. `System.out.println(sum);` 将结果打印到控制台上。 所以,程序的输出结果为 `15`。 * * * * */ }
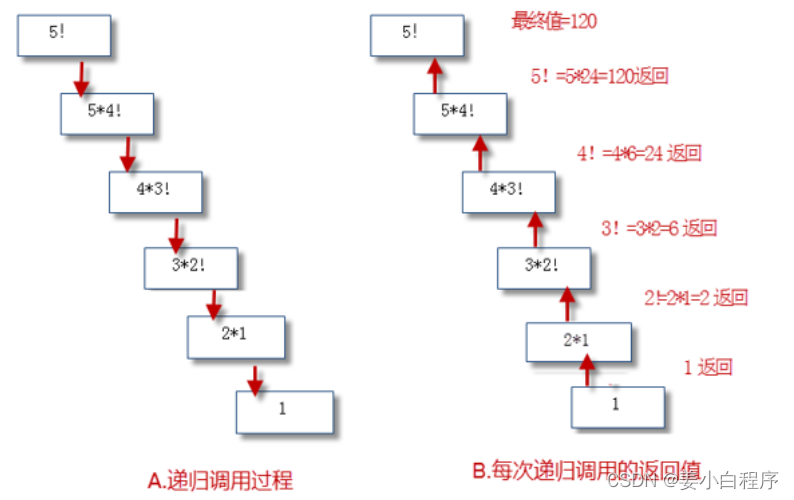
举例2:递归方法计算n!
public int multiply ( int num ){if ( num == 1 ){return 1 ;} else {return num * multiply ( num - 1 );}}
public int f ( int num ){if ( num == 0 ){return 1 ;} else if ( num == 1 ){return 4 ;} else {return 2 * f ( num - 1 ) + f ( num - 2 );}}
举例3:已知有一个数列:f(0) = 1,f(1) = 4,f(n+2)=2*f(n+1) + f(n),其中n是大于0的整数,求f(10)的值。
public int func ( int num ){if ( num == 20 ){return 1 ;} else if ( num == 21 ){return 4 ;} else {return func ( num + 2 ) - 2 * func ( num + 1 );}}
举例4:计算斐波那契数列(Fibonacci)的第n个值
斐波那契数列满足如下规律,
1
,
1
,
2
,
3
,
5
,
8
,
13
,
21
,
34
,
55
,....
即从第三个数开始,一个数等于前两个数之和。假设
f(n)
代表斐波那契数列的第
n
个值,那么
f(n)
满足:
f(n) = f(n-2) + f(n-1);
// 使用递归的写法int f ( int n ) { // 计算斐波那契数列第 n 个值是多少if ( n < 1 ) { // 负数是返回特殊值 1 ,表示不计算负数情况return 1 ;}if ( n == 1 || n == 2 ) {return 1 ;}return f ( n - 2 ) + f ( n - 1 );}// 不用递归int fValue ( int n ) { // 计算斐波那契数列第 n 个值是多少if ( n < 1 ) { // 负数是返回特殊值 1 ,表示不计算负数情况return 1 ;}if ( n == 1 || n == 2 ) {return 1 ;}// 从第三个数开始, 等于 前两个整数相加int beforeBefore = 1 ; // 相当于 n=1 时的值int before = 1 ; // 相当于 n=2 时的值int current = beforeBefore + before ; // 相当于 n=3 的值// 再完后for ( int i = 4 ; i <= n ; i ++ ) {beforeBefore = before ;before = current ;current = beforeBefore + before ;/* 假设 i=4beforeBefore = before; // 相当于 n=2 时的值before = current; // 相当于 n=3 的值current = beforeBefore + before; // 相当于 n = 4 的值假设 i=5beforeBefore = before; // 相当于 n=3 的值before = current; // 相当于 n = 4 的值current = beforeBefore + before; // 相当于 n = 5 的值....*/}return current ;}
举例5:面试题
宋老师,我今天去百度面试,遇到一个一个双重递归调用的问题,我琢磨了一下,完全不知道为什
么。打断点了,也还是没看懂为什么程序会那样走。您有空可以看一下,求指教。
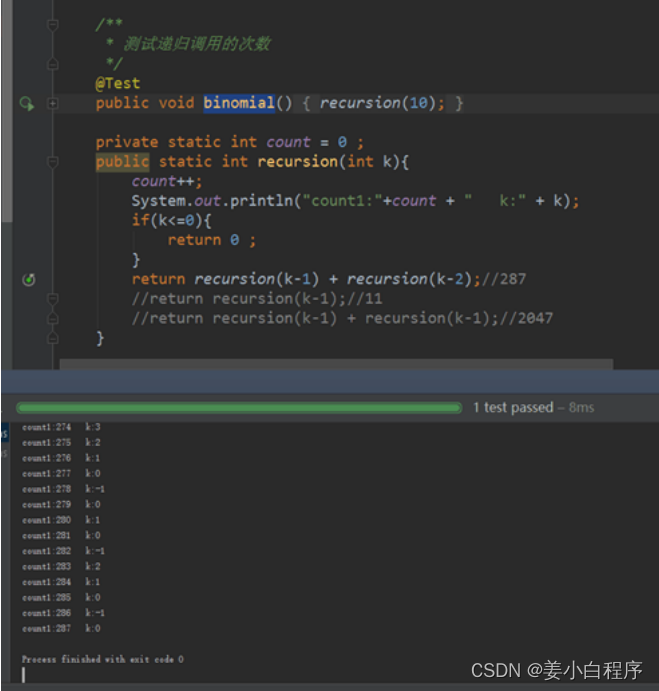
private int count = 0 ;public int recursion ( int k ) {count ++ ;System . out . println ( "count1:" + count + " k:" + k );if ( k <= 0 ) {return 0 ;}return recursion ( k - 1 ) + recursion ( k - 2 ); //287//return recursion(k - 1);//11//return recursion(k - 1) + recursion(k - 1);//2047}
剖析:
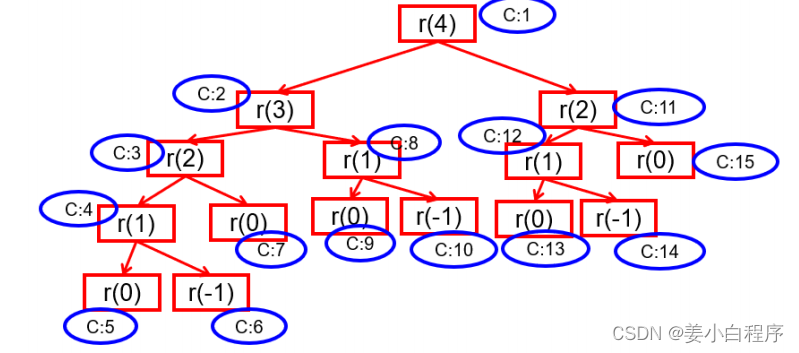
最后说两句:1. 递归调用会占用大量的系统堆栈,内存耗用多,在递归调用层次多时速度要比循环 慢的多 ,所以在使用递归时要慎重。2. 在要求高性能的情况下尽量避免使用递归,递归调用既花时间又 耗内存 。考虑使用循环迭 代。


![每日一题 --- 快乐数[力扣][Go]](https://img-blog.csdnimg.cn/direct/f118c99ed8fa4c7e8605e59ee937ce7b.png)