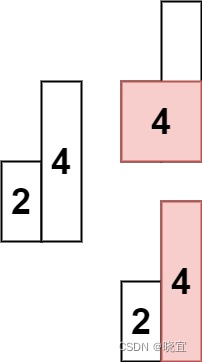
Hash

哈希算法：
    在记录的 存储位置 和它的 关键字 之间建立一种去特定的对应关系，使得每个关键字key对应一个存储位置；
    查找时，根据确定的对应关系，找到给定的 key 的映射。
    
        记录的存储位置 = f（关键字）
        
    我们把这种关系 f 称为  哈希函数（散列函数）；
     哈希表：                                                                                                                                                          采用这种 散列技术 将记录存储在一块  连续的存储空间，这块连续存储开空间称为哈希表或散列表。
    
    存储时，通过  散列函数  计算出记录的  散列地址；
    查找时，根据同样的  散列函数  计算记录的  散列地址，并按此  散列地址访问 记录。

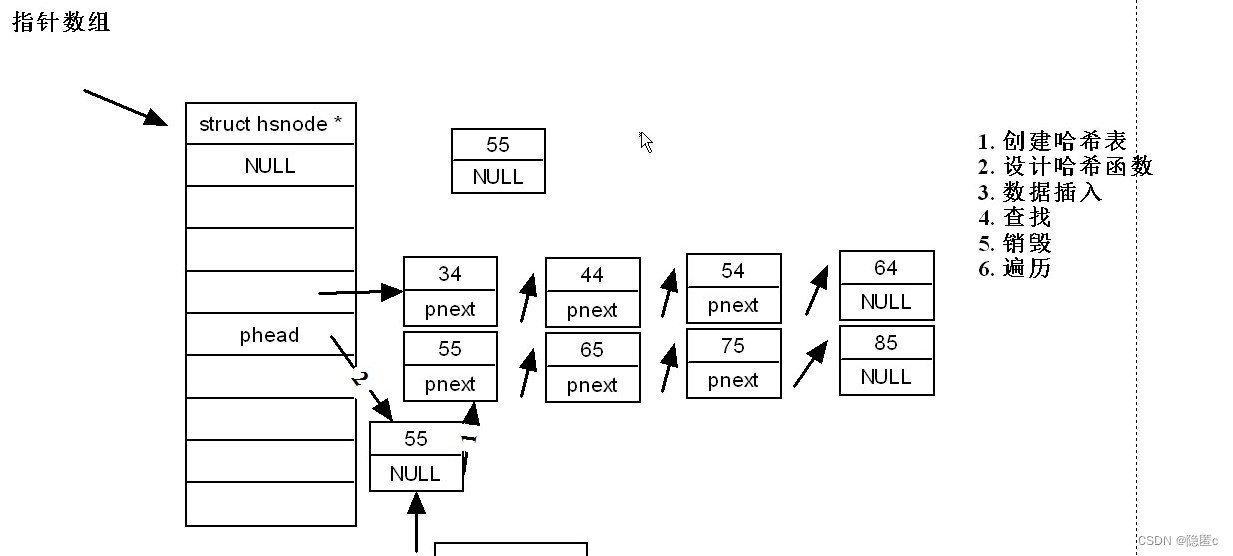
                           存地址的数组 hash_table[addr] ==>phead  功能

 
算法：
   解决特定问题求解步骤
   
   
   算法的设计，
    1.正确性，
        语法正确
        合法的输入能得到合理的结果。
        对非法的输入，给出满足要求的规格说明
        对精心选择，甚至刁难的测试都能正常运行，结果正确
    2. 可读性，便于交流，阅读，理解    高内聚 低耦合
    3. 健壮性，输入非法数据，能进行相应的处理，而不是产生异常
    4. 高效率  (时间复杂度)      
    5. 低存储（空间复杂度）

    算法时间复杂度
        执行这个算法所花时间的度量
        
        将数据量增长和时间增长用函数表示出来，这个函数就叫做时间复杂度。
        一般用大O表示法：O（n）-----时间复杂度是关于数据n的一个函数
        随着n的增加，时间复杂度增长较慢的算法时间复杂度低
    时间复杂度的计算规则
        1，用常数1 取代运行时间中的所有加法常数
        2，在修改后的运行函数中，只保留最高阶项。
        3，如果最高阶存在且系数不是1，则去除这个项相乘的常数。
        
        Fun(int a,int b)       O(1)
        {
    3        Int tmp = a;          O（1）    n              O（1）
            A = b;
            B = tmp;
        }
        for(i=0;i<n;i++)        O(n)     n       O(n)
        {
    3n        Int tmp = a;
            A = b;
            B = tmp;             O(n）
        }

        
        for (i = 1; i < n; i *= 2)    O(logn)      1*2*2*2*2*2... < n
    x    {
                                    2 ^x = n
                                 o(logn)
        }
        for(i=0;i<n;i++)        O(nlogn)    
        {
                for (i = 0; i < n; i *= 2)    o(logn)
                {
                                 
                }
        }
        
        
        for(i=0;i<n;i++)       o(n^2)
        {                                    
             for(j=i;j<n;j++)                    0    1        2              ...n-1
            {                                     
                Int tmp = a;                   3n   3(n-1)   3(n-2)             3
    n^2            A = b;                         
                B = tmp;                        3 (n + 1)n/2  ====>n^2
            }
        }
        
        O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
    

排序算法：

是否稳定：数据是否交换
                                                

                                                                 冒泡排序（稳定）

选择排序

                                                               

插入排序

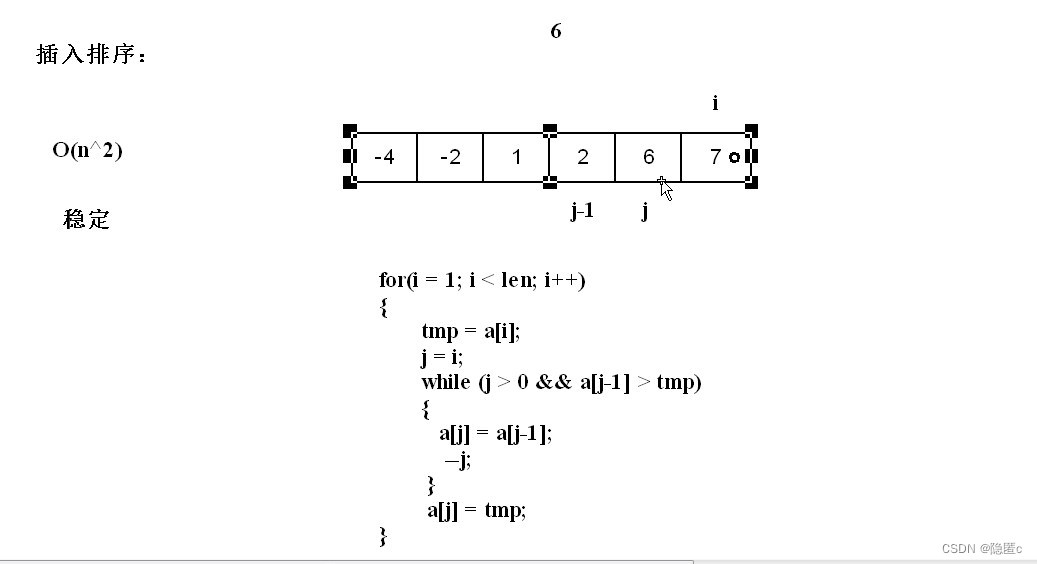
快速排序

二分查找：有序序列为前提，O(logn)时间复杂度