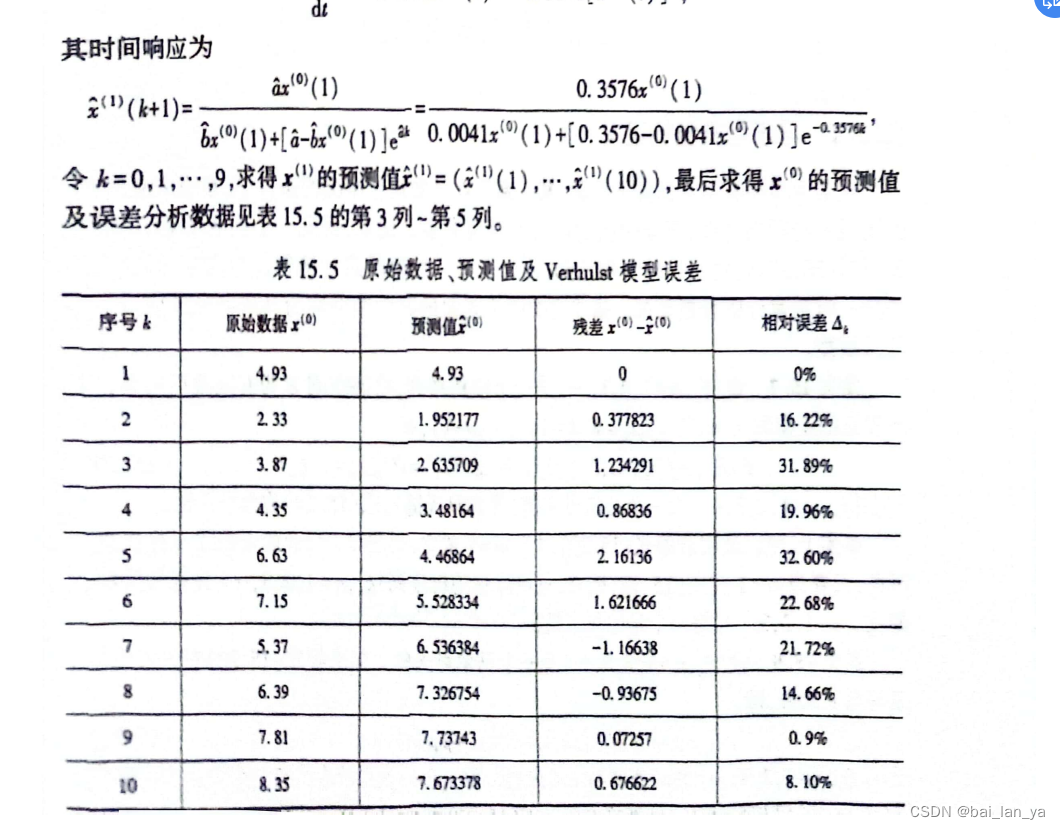
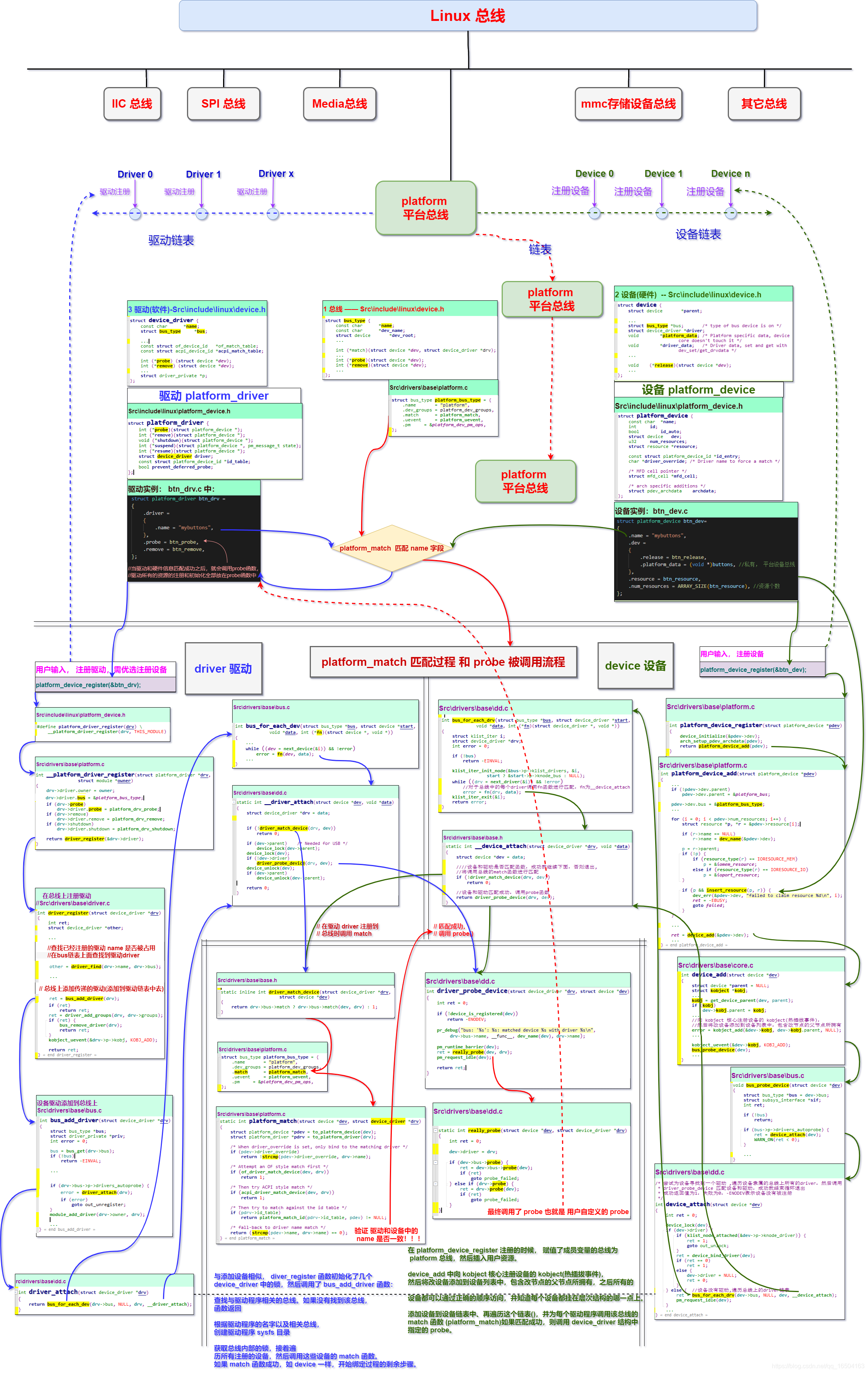
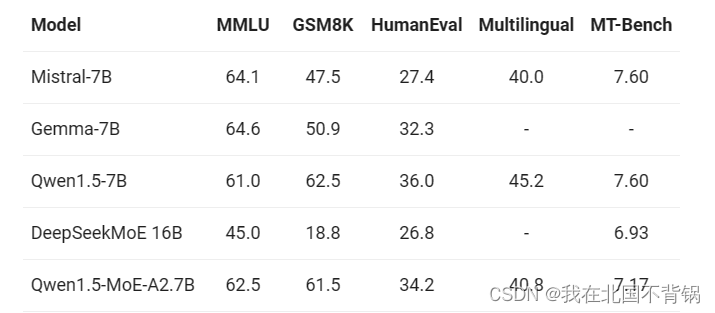
1,灰色系统简介
著名学者邓聚龙教授于20世纪70年代末、80年代初提出:
“ The诞生标志:邓教授第一篇灰色系统论文Control Problems of Grey Systems”,发表于北荷兰出版公司期刊 System & Control Letter,1982, No.5.
1.1 灰色系统,白色系统,黑色系统
- 白色系统是指一个系统的内部特征是完全已知的,即系统的信息是完全充分的。
- 黑色系统是指一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以观测研究。
- 灰色系统内的一部分信息是已知的,另一部分信息是未知的,系统内各因素间有不确定的关系。
1.2 灰色系统理论的主要内容
灰色系统理论经过20多年的发展,已基本建立起了一门新兴学科的结构体系,其主要内容包括以“灰色朦胧集”为基础的理论体系、以灰色关联空间为依托的分析体系、以灰色序列生成为基础的方法体系以灰色模型(GM)为核心的模型体系。以系统分析、评估、建模、预测、决策、控制、优化为主体的技术体系。
1.3 灰色系统理论的研究对象
“部分信息已知,部分信息未知”的“小样本、贫G信息”不确定性系统。
1.4 灰色系统理论的研究内容
灰哲学、灰生成、灰分析、灰建模、灰预测、灰决策、灰控制、灰评估、灰数学等。
1.5 灰色系统理论的应用领域
农业科学、经济管理、环境科学、医药卫生、矿业工程、教育科学、水利水电、图像信息、生命科学控制科学等。
1.6 比较
因素分析的基本方法过去主要采取回归分析、方差分析,主成分分析等办法,但是这种方法需要大量数据作为基础,计算量大。
而灰色系统理论采用的关联分析方法可以克服这个弊端。
灰色系统理论进行系统分析的方法:关联度分析法
2,关联度分析法
2.1 关联分析的背景
客观世界中的事物往往现象复杂,因素繁多。我们往往需要对系统进行因素分析,这些因素中哪些对系统来讲是主要的,哪些是次要的,哪些需要发展,哪些需要抑制,哪些是潜在的,哪些是明显的。一般来讲,这些都是我们极为关心的问题。事实上,因素间关联性如何、关联程度如何量化等问题是系统分析的关键和起点。
2.2,灰色关联分析法
- 灰色关联分析是灰色系统理论的一个分支,应用灰色关联分析方法对受多种因素影响的事物和现象从整体观念出发进行综合评价是一个被广为接受的方法.
- 基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近,相应序列之间关联度就越大,反之就越小。
2.3 灰色关联分析法的步骤
利用灰色关联分析进行综合评价的步骤是:
1.3.1.根据评价目的确定评价指标体系,收集评价数据。
设n个数据序列形成如下矩阵:
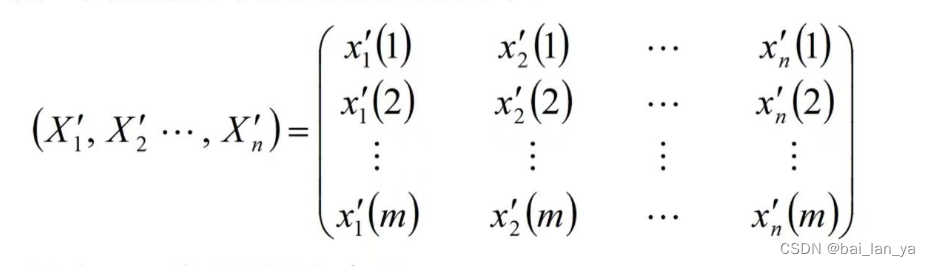
其中m 为指标的个数:

2.3.2 确定参考数据列参考数据列
应该是一个理想的比较标准可以以各指标的最优值(或最劣值)构成参考数据列,也可根据评价目的选择其它参照值,记作

2.3.3 常用的无量纲化方法
常用的无量纲化方法有均值化法(见(12-3)式)、初值化法(见(12-4)式)

2.3.4 逐个计算每个被评价对象指标序列
(比较序列)与参考序列对应元素的绝对差值即|x(k)-x(k)|(k=1…,mi=1.…n)n为被评价对象的个数)
2.3.5

2.3.6.计算关联系数
由(12>5)式,分别计算每个比较序列与参考序列对应元素的关联系数

式中p为分辨系数,在(0,1)内取值,若越小,关联系数间差异越大,区分能力越强。通常p取0.5

2.3.7.计算关联度
对各评价对象(比较序列)分别计算其个指标与参考序列对应元素的关联系数的均值,以反映各评价对象与参考序列的关联关系,并称其为关联度,记为:
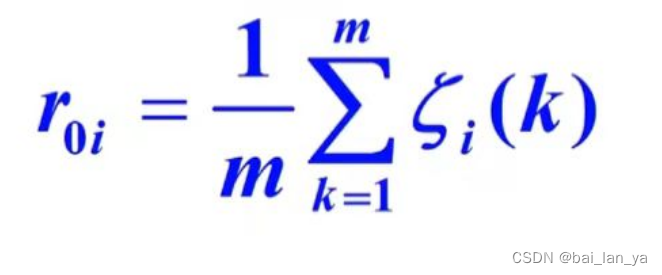
3.灰色关联分析的应用举例。
例1:利用灰色关联分析对6位教师工作状况进行综合评价
1.评价指标包括:专业素质、外语水平、教学工作量科研成果、论文、著作与出勤.
2.对原始数据经处理后得到以下数值,见下表

3.确定参考数据列:

4.计算x0(k)-xi(k),见下表
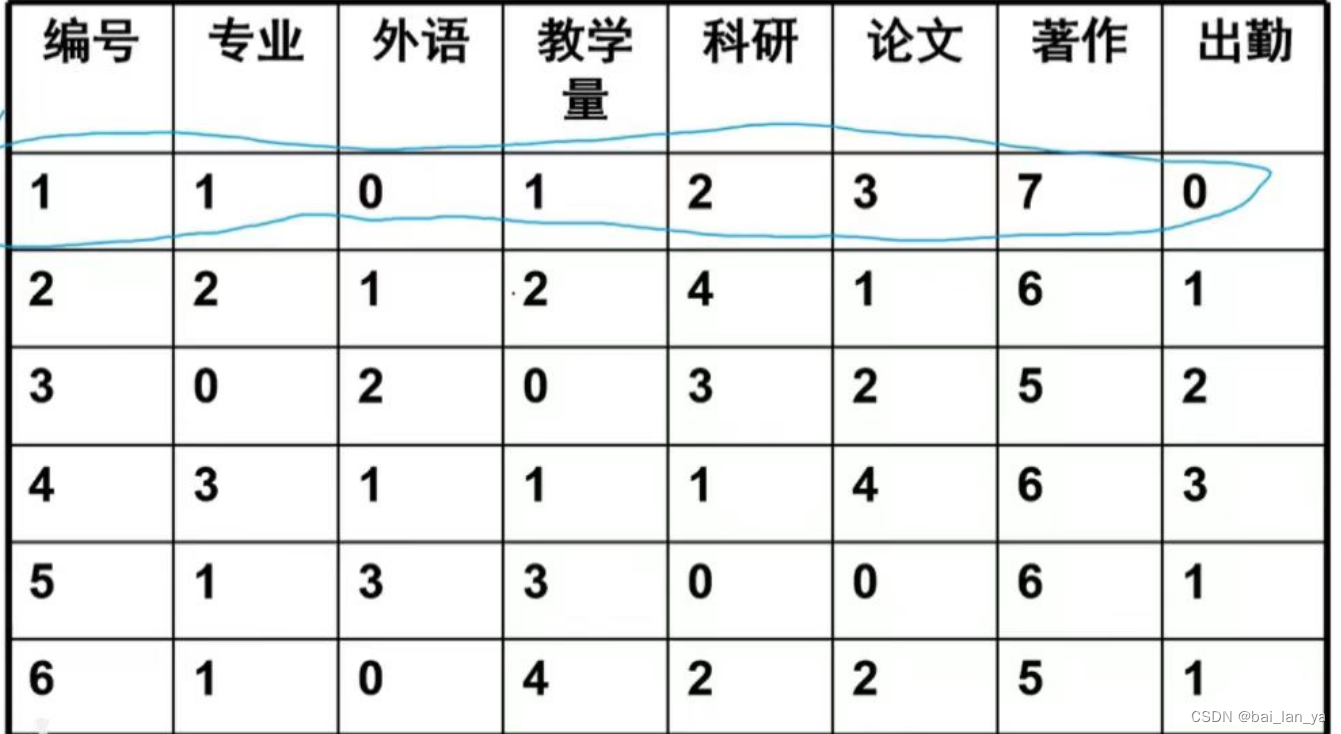
5,求最值

6.依据(12-5)式,p-0.5取计算,得

8.如果各指标在综合评价中所起的作用不同,可对关联系数求加权平均值即

9.依据各观察对象的关联度,进行排序,得出综合评价结果
小结(灰色关联分析法)
优点:
灰色关联分析法弥补了采用数理统计方法作系统分析所导致的遗憾。它对样本量的多少和样本有无规律都同样适用,而且计算量小,十分方便,更不会出现量化结果与定性分析结果不符的情况。缺点:
要利用该方法,这个系统必须是灰色系统。灰色系统中灰的主要含义是信息不完全性(部分性)和非唯一性,其中的“非唯一性”是灰色系统的重要特征,非唯一性原理在决策上的体现是灰靶思想,即体现的是决策多目标、方法多途径,处理态度灵活机动
4,灰色综合评价简介
灰色综合评价法是针对复杂大系统进行效能评估时,信息不完备、不全面、不充分的情况,所提出的一种评估方法,其基于灰色关联度分析
可分为:
单层次灰色综合评价
多层次灰色综合评价
4.1 单层次灰色综合评价
设有m个评价对象,每个评价对象有n个评价指标,第i个评价对象的第i个指标为
y(i=1,2,…,m;j=1,2,…,n)
4.1.1 确定最优指标集

4.1.2 构造原始矩阵
用最优指标集和评价对象的指标构成原始矩阵

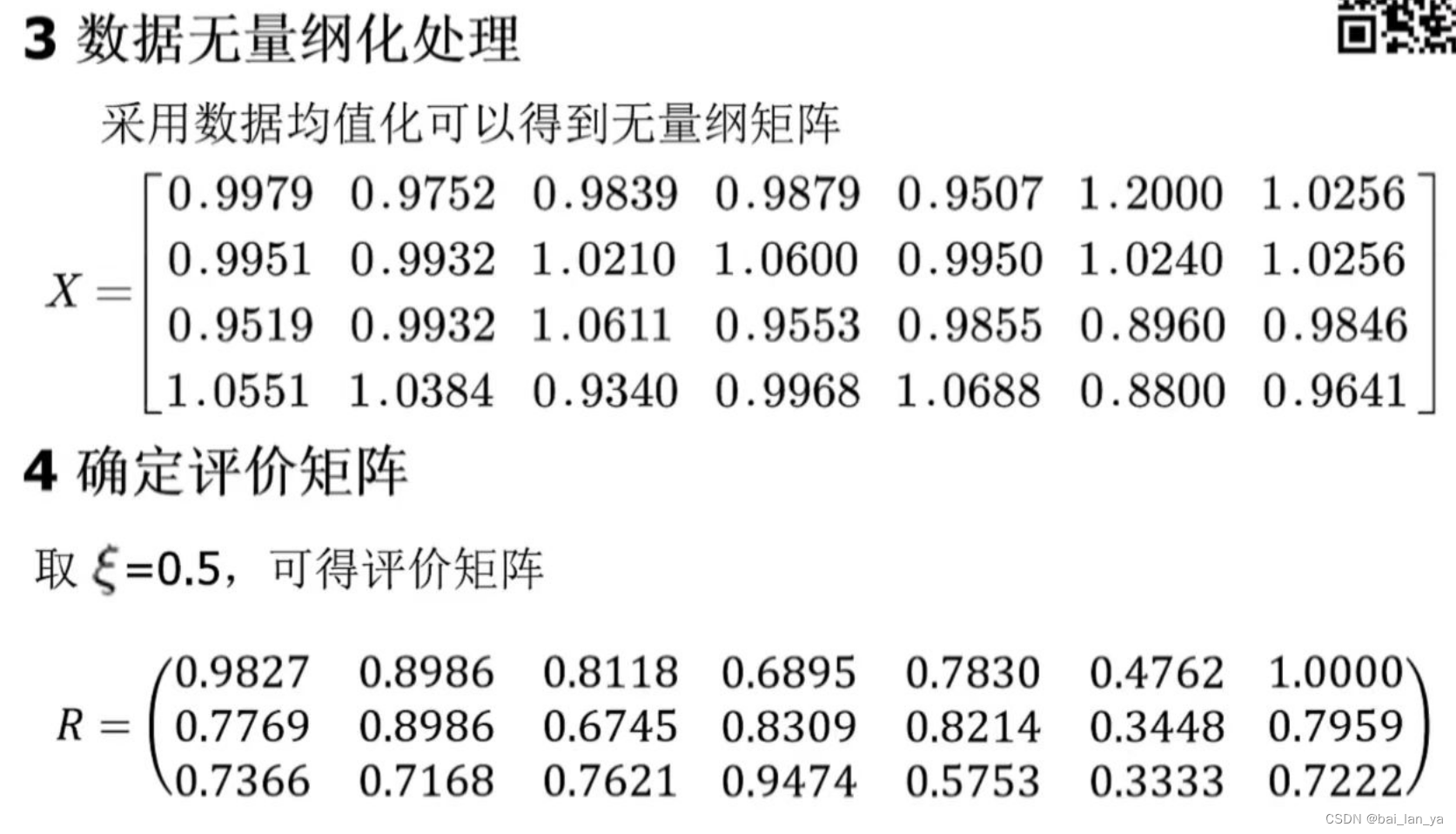
4.1.3 数据无量纲化处理
采用数据均值化处理,即将矩阵y的每列所有数据除以该列数据的平均值,即
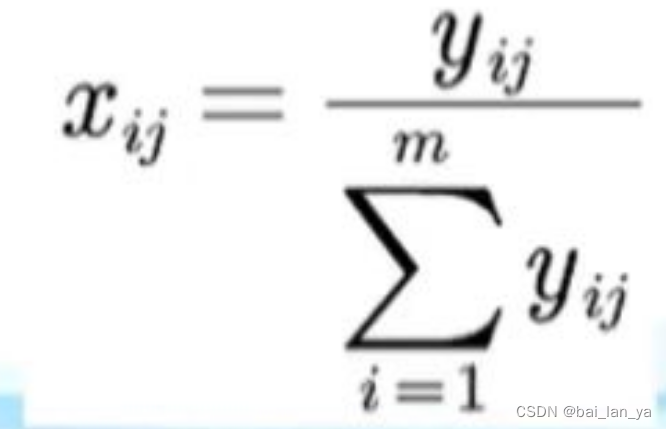
4.1.4 确定评价矩阵
以最优指标集为参考序列,各评价对象的指标为比较序列,计算第i个评价对象与第j个最优指标的灰色关联系数。
4.1.5灰色关联系数计算
利用下式计算
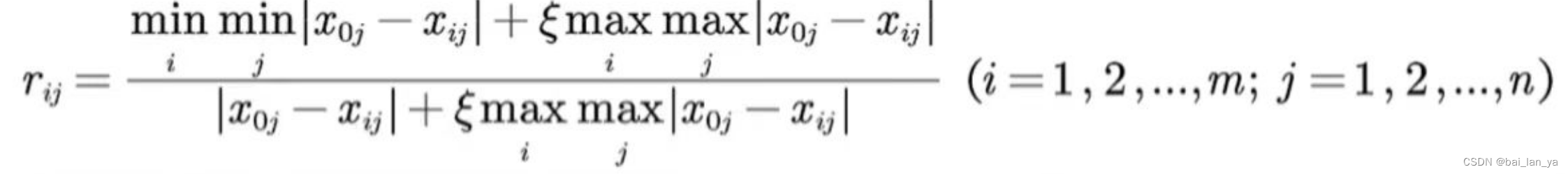
4.1.6 确定各评价指标的权重矩阵 Wj
依据各指标重要程度为其赋予相应权重Wj
4.1.7计算灰色关联度矩阵
各评价对象与最优指标之间的关联系数ri组成评价矩阵R,计算灰色关联度矩阵A:

其中,各评价对象的灰色关联度

灰色关联度越大,说明其相应的评价对象越接近于最优指标,据此便可排出各评价对象的优劣顺序。
4.多层次灰色综合评价及步骤
当评价对象的指标体系由不止一个层次构成时,需采用多层次综合评价模型。
多层次综合评价在单层次综合评价基础上进行,评价方法与单层次评价模型相似。
比如,第二层次的灰色关联度矩阵组成第一层次的评价矩阵,计算出第一层次的灰色关联度矩阵,进而得出评价结果,依次类推。
例1 单层次灰色综合评价例题
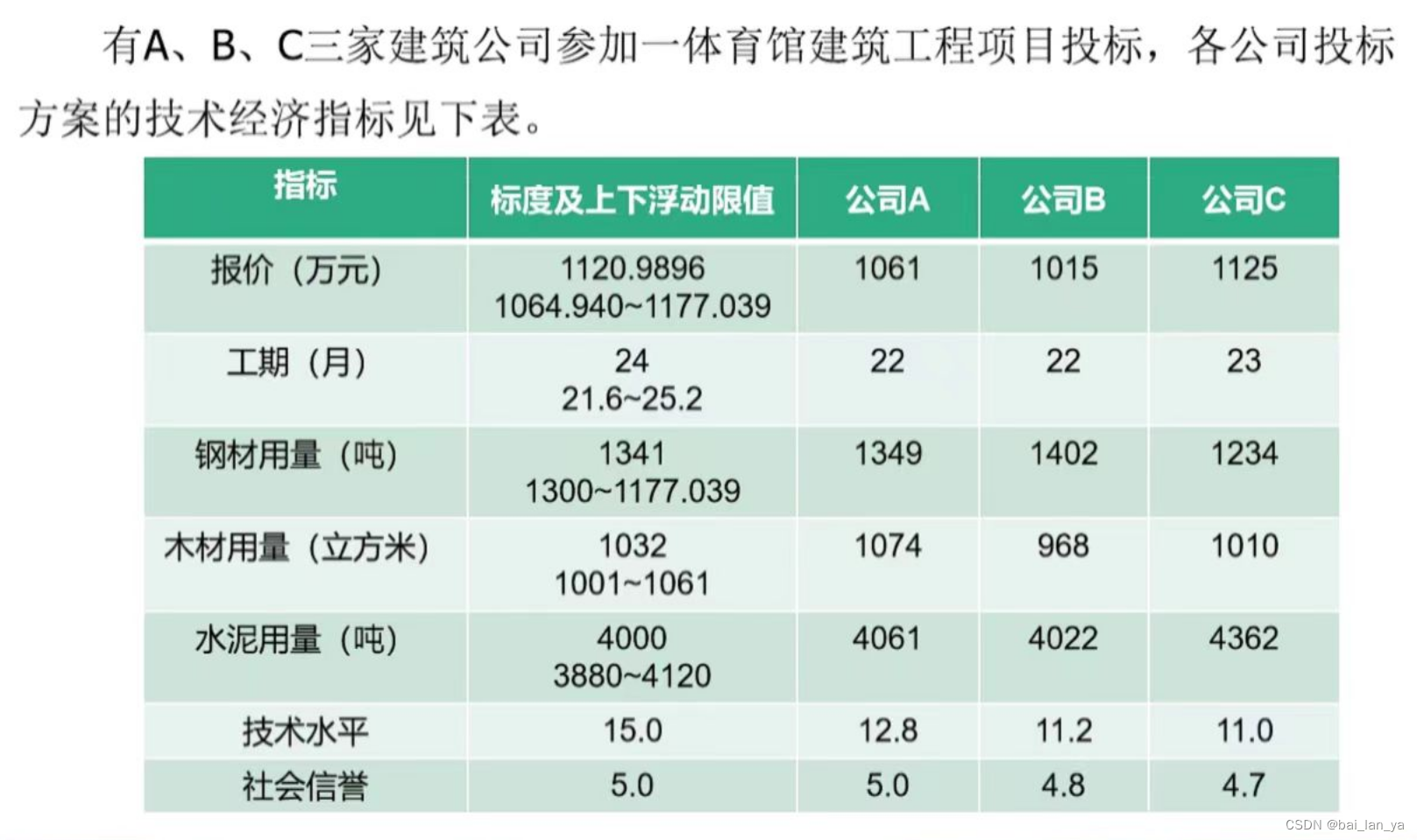
解答:


总结:
优点:
计算方法简单,综合能力较强,准确度较高,可以决定对象所属的设定类别。
缺点:
白化权函数较难确定
例题及用matlab解题


 matlab程序如下:
matlab程序如下:
clc,clear
x0=[41,49,61,78,96,104];%原始序列
n=length(x0);
x1=cumsum(x0);%计算1 次累加序列
a_x0=diff(x0);%计算1 次累减序列
z=0.5*(x1(2 :end)+x1 (1:end-1))';%计算均值生成序列
B=[-x0(2:end)',-z,ones(n-1,1)];
u = B\a_x0;%最小二乘法拟合参数
syms x(t);
x=dsolve(diff(x,2)+u(1)*diff(x)+u(2)*x==u(3),x(0)==x1(1),x(5)==x1(6));
%求符号解
xt=vpa(x,6);%显示小数形式的符号解
yuce=subs(x,t,0:n-1);%求已知数据点1次累加序列的预测值
yuce=double(yuce);%符号数转换成数值类型,否则无法做差分运算
x0_hat=[yuce(l),diff(yuce)];%求已知数据点的预测值
x0_hat =round(x0_hat);%四舍五入取整效
epoilon=x0-x0_hat;%求残差
delta=aba(epsilon./x0);%求相时误差