🎀个人主页： https://zhangxiaoshu.blog.csdn.net
📢欢迎大家：关注🔍+点赞👍+评论📝+收藏⭐️，如有错误敬请指正!
💕未来很长，值得我们全力奔赴更美好的生活！

前言

支持向量机（SVM）是一种强大的监督学习算法，常用于分类和回归分析。在POLSAR图像分类中，SVM可以被有效地应用。支持向量机具有对高维数据的处理能力、对于非线性分类问题的适应性、泛化能力强等优点，本文为基于SVM实现PLOSAR图像分类的一个小实例。

---

---

一、数据预处理

对于提供的原始数据ALLData.mat和标签数据label.mat来说，标签数据是包含背景0的，所以，在分类之前，我们首先需要将对应label为0的对于提供的原始数据删除。将原始数据ALLData.mat和标签数据label.mat读取并查看维度信息如下所示：

#读取mat数据
data_orginal = io.loadmat(r"D:/VSCode/Task_python/lab/homework/Image classification/PolSAR/ALLData.mat")["ALLData"]
label_original = io.loadmat(r"D:/VSCode/Task_python/lab/homework/Image classification/PolSAR/label.mat")["label"]
label = np.reshape(label_original, data_orginal.shape[0], order='F')

print("ALLData shape=",data_orginal.shape)
print("label shape=",label.shape)

输出为：

ALLData shape= (768000, 9)
label shape= (768000,)

可以看到ALLData和label共有768000条数据，其中ALLData的每一条数据是一个1*9的向量，label为一个数，为了后续清零操作的便利，我们将这两个数据拼接在一起，即使用：

data_o=torch.cat([torch.tensor(data_orginal),

torch.tensor(label).reshape(768000,1)],-1).numpy()，

这样我们便得到了一个768000*10的序列。

下面进行清零操作，首先，我们定义一个data数据，将第一个label不为0的数据赋值给data，之后遍历读取的原始拼接在一起的数据data_o，如果data_o[i][9]不等于0，我们就将data_o[i]拼接到data中，最后保存data，操作过程如下所示。

#数据清零
data=data_o[111135]
for i in range(111136,768000-1):
    if data_o[i][9]!=0:
        data=np.vstack((data,data_o[i]))
np.save('data.npy',data)

清零完成后，我们便得到了一个167712*10的数据，其中前9列是数据，后面一列为标签。

二、基于SVM的PLOSAR图像分类

1. SVM简介

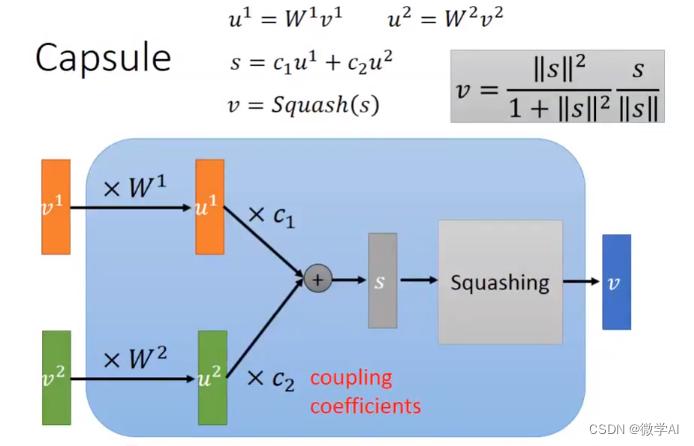
支持向量机（Support Vector Machine，SVM）是一种强大的监督学习算法，用于分类和回归分析。它的主要思想是找到一个最优的超平面，将不同类别的样本在特征空间中分隔开来，并且使得两侧距离最近的样本点到超平面的距离最大化。这些最接近超平面的样本点被称为支持向量，因此SVM也被称为最大间隔分类器。

SVM算法的基本原理和步骤如下：

• 数据准备：获取带有标签的训练数据集，每个样本包含特征和对应的类别标签。

• 选择核函数：SVM利用核函数来将数据从原始特征空间映射到更高维的特征空间，以便在高维空间中找到一个最优的超平面。常用的核函数包括线性核、多项式核、高斯核等。

• 构建优化问题：SVM的目标是找到一个最优的超平面，使得间隔最大化，并且能够正确地分类训练数据。这可以转化为一个凸优化问题，通常通过求解拉格朗日对偶问题来实现。

• 求解优化问题：通过优化算法（如序列最小最优化算法，SMO）来求解构建的优化问题，找到最优的超平面参数。

• 分类预测：对于新的未知样本，根据构建好的超平面参数和核函数来预测其类别。样本被分类到距离超平面一侧的类别中。

2. 分类实验

定义一个SVM分类器，这里我们直接使用sklearn来实现，然后我们的实验分别测试了当训练数据集比例为[0.1,0.3,0.5]时的准确率，同时测试了kernel的取值分别为[‘poly’,‘linear’,‘rbf’,‘sigmoid’]的准确率，共九组实验，其中实验过程代码如下所示，

acc=[]
kernel=['poly','linear','rbf','sigmoid']
train_size=[0.1,0.3,0.5]
for i in range(4):
    print("kernel=",kernel[i],"时：")
    for j in range(3):
        #划分训练集和测试集
        X_train,X_test,y_train,y_test = train_test_split(data, label, train_size=train_size[j], stratify=label)
        svm_model = SVC(kernel = kernel[i])
        svm_model.fit(X_train, y_train.reshape((-1, 1)).ravel())
        y_predict = svm_model.predict(X_test)
        acc.append(accuracy_score(y_test, y_predict))
        print("train_size=",train_size[j], "的分类准确率为: ", acc[i*3+j])

结果为：

• kernel= poly 时：
  train_size= 0.1 的分类准确率为: 0.6073366414691833
  train_size= 0.3 的分类准确率为: 0.6382166798695048
  train_size= 0.5 的分类准确率为: 0.7034797748521274
• kernel= linear 时：
  train_size= 0.1 的分类准确率为: 0.13331036630206505
  train_size= 0.3 的分类准确率为: 0.1748396494007615
  train_size= 0.5 的分类准确率为: 0.22277475672581568
• kernel= rbf 时：
  train_size= 0.1 的分类准确率为: 0.8272570077049973
  train_size= 0.3 的分类准确率为: 0.8719409875722962
  train_size= 0.5 的分类准确率为: 0.8772180881511162
• kernel= sigmoid 时：
  train_size= 0.1 的分类准确率为: 0.3574575496386005
  train_size= 0.3 的分类准确率为: 0.3508632952580516
  train_size= 0.5 的分类准确率为: 0.3413947719900782

实验数据如表所示。从实验结果中我们可以看到，使用SVM分类器的分类效果没有KNN的效果好，不同的kernel函数准确率差距较大，使用linear时，最高只有22%的准确率，但是在kernel函数为rbf时，其最高准确率可以达到87%。同时，我们可以看到，对于不同的训练数据集比例来说，较大的数据集更加能学习到更好的分类特征，这和KNN是一样的。对于不同的kernel函数来说，我们可以看到不同的kernel函数会对模型的准确度产生严重的影响，所以kernel函数的取值往往需要一个合适值，例如，在这一分类问题中rbf kernel函数相对其它kernel函数准确度更好。

train_size=0.1	train_size=0.3	train_size=0.5
poly	0.6071908891553653	0.6418964386408743
linear	0.13326399056585023	0.1747459518394535
rbf	0.8318614558006109	0.8727587117437117
sigmoid	0.394200382931079	0.40387056107803304

最后，我们使用训练好的模型将原始数据读入，并将分类的结果绘制成图片的形式，其结果如下图所示。

结合KNN的实验结果从整体上两个分类器所表现的行性能来看，KNN相对来说更加稳定一些，在KNN实验中，无论K的取值如何，它的最终结果总是保持在85-87%之间，但是反观SVM来说，它受kernel函数取值的影响太多，例如，在kernel函数为rbf时，其最高准确率可以达到87%。但是在kernel函数为linear时，最高准确率仅仅只有达到22%。总的来说，SVM分类器受到kernel函数很大程度上的影响。

---

文中有不对的地方欢迎指正、补充。