欢迎来到博主的专栏——C语言数据结构
博主ID：代码小豪

排序

现在有N个数据的序列，其对应的序列号为[r₁ ,r₂ ……r_n];将该序列对应的数据[k₁ ,k₂ ……k_n]排成满足递减或递减的序列的操作称为排序

插入排序

玩过斗地主的小伙伴都有过这种经历吧，拿到的牌是一些无序的牌组，这时候很难发现卡牌之间的组合，比如顺子、飞机。如果我们将牌顺好之后，牌与牌之间的关系就变得显而易见了。（顺牌：将扑克牌的点数排成升序或者降序）。

不知道大伙顺牌的方式是不是和我一样，比如一个点数为7的牌在大王的后面，我就将这个7插入与7最接近的两个点数的扑克牌之间。

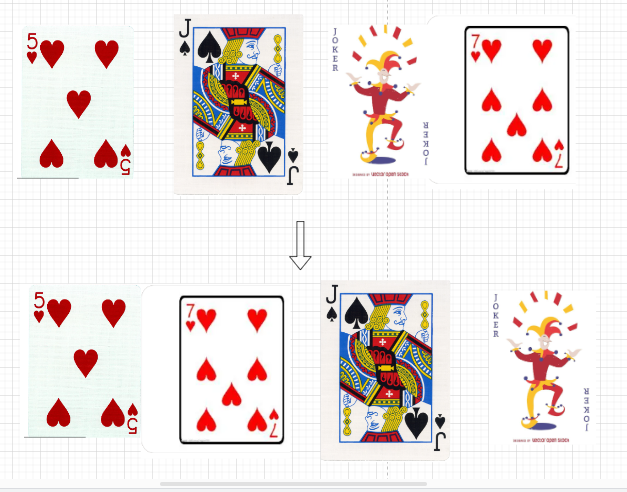
这个过程是怎样的呢？首先比较7和大王，7比大王小，向后比较，比较7和J，7比J小，向后比较，最后比较7和5, 7比5大，将7插入到5的后面。

细心观察可以发现，7之间的扑克牌已经升序排列了，这和平时打牌的时候一样，将7插入到5与J之间的前提是不是已经将5与J排好了才能插入？对于人来说，这是一个很简单的操作，因为人脑可以随机应变的将5与J拍好序，但是对于机器来说，它是需要一个固定的操作来完成的。我们需要一个稳定的逻辑来实现这种插入排序。

还是回到扑克牌，现在将这个牌型变得更加无序。

现在该如何用插入排序将这堆牌排成升序呢？

前面将7进行插入排序的时候，需要让7之间的扑克牌点数处于升序状态，从这里可以提炼出一个信息。

（1）若是想要用插入排序将一组数据排成升序，就要先将这个数据的前边数据排成升序
（2）结束插入排序后，这组数据会构成升序。

假如现在有N个数据，那么这N个数据用插入排序算法的思路就应该如下：

（1）为了让n能使用插入排序，将前n-1个数据排成升序，这样就能让n个数据排成升序
（2）为了让n-1个数据能构成升序，对n-1进行插入排序，这就需要先让前n-2个数据排成升序
……
（N-1）为了让前2个数据排成升序，就需要对第2个数据使用插入排序，此时就不存在前一个数据不符合升序的问题了。第一个数据无论如何都满足升序的要求。

从这里可以推断出，如果从第二个数据开始使用插入排序，一直到第N个数据，那么这堆数据就可以完成排序。

回到扑克牌，我们需要从第二张牌开始进行插入排序

7比大王小，继续往前比较，但是此时前面不在有点数了，于是将7放在大王的前面
5比大王小，继续向前比较，5又比7小，将5插入至7的前面。

j比大王小，继续向前比较，j比7大，插入至7的后面。

此时就完成了4个扑克牌的排序。

插入排序的代码如下：

void InsertSort(int* a, int n)//a是待排序数组，n是数组的元素个数
{
	int end = 0;
	for (int i = 1; i < n ; i++)
	{
		end = i;//从第2个数据开始插入排序，一直到第n个数，构成排序
		int tmp = a[end];//将进行插入排序的数据进行保存，方便找到位置后进行插入
		while (end > 0)
		{
			if (tmp < a[end - 1])
			{
				a[end] = a[end - 1];//将不符合条件的数据向后移动一位，空出空间。
				end--;//继续往前比较
			}
			else//找到适合的位置就退出循环，此时end位于合适的位置
			{
				break;
			}
		}
		a[end] = tmp;
	}
}

希尔排序

希尔排序是插入排序的改进版本，由Shell提出的一种排序算法。插入排序在某种情况下会变得高效，比如数据本就升序或者接近升序的状态，此时插入排序的时间复杂度接近O（N），而非常规情况下的O（N²）。

希尔排序就是利用了这个特点，如果我们可以在进行插入排序之前，先将无序的数据排列的接近有序，这样子插入排序的效率就会变得更高。

如何将数据变得接近有序呢？希尔排序中采用了一种预排序的方法，通过预排序可以简单的想将数据排列成接近有序的序列。预排序的思路如下：

（1）将整个序列分成多个子序列
（2）将子序列的的数据排成有序

那么问题就在于如何分割子序列了：现在有这么一堆无序数据： { 5,3,4,6,7,9,1,8,2 };我们简单将该序列分成3组{5,3，4}，{6,7，9}，{1,8，2}。进行预排序后的子序列变成{3，4，5}，{6，7，9}，{1，2，8}，合并子序列后的数据变成{3，4，5，6，7，9，1，2，8}，这个序列显然是不符合接近有序这个要求的。

想要序列变成接近有序，就需要让大的数据排在后面，小的数据排在前面，这样子的预排序才是有效的，于是希尔想出的预排序方法如下：
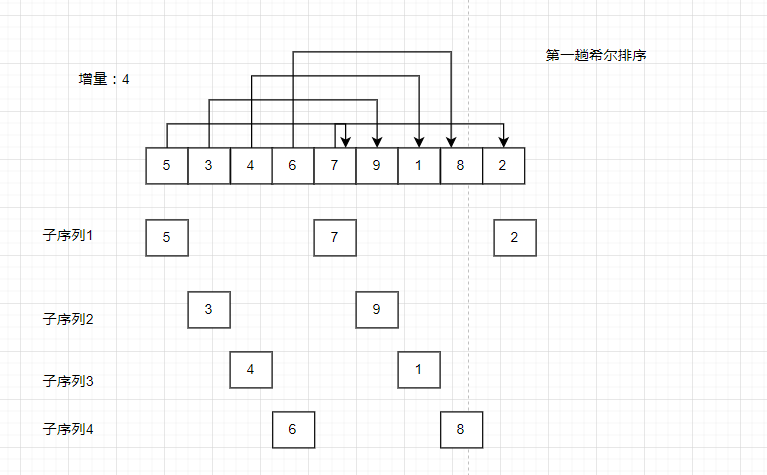
子序列不再是相邻的，而是跳跃的.,让相距某个增量的数据组成子序列。

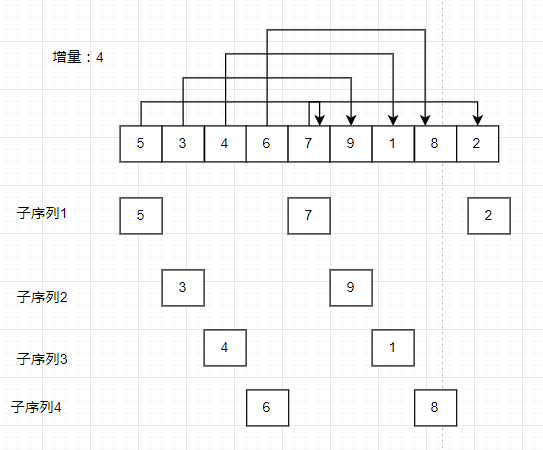
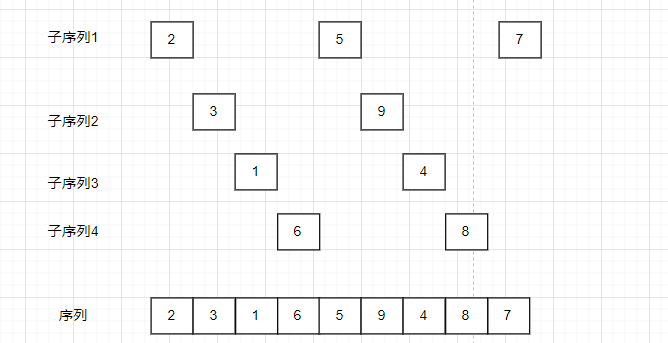
将子序列进行排序后的序列为

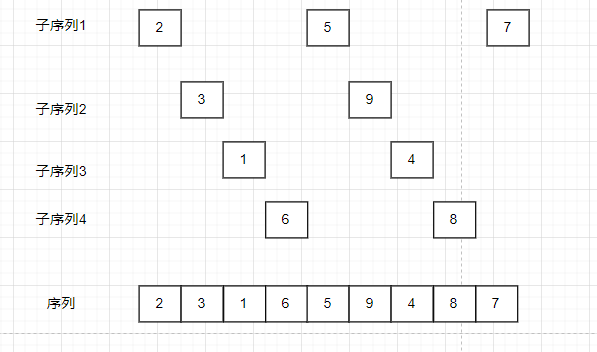
可以发现这个序列比预排序之前的序列更加有序。如果再对这个序列进行增量更小的预排序，这个序列将会更加更近有序。

那么如何选择预排序的增量呢？常用的方法有两个：一个是让增量等于前一次预排序的增量的一半，另外则是让增量等于前一次预排序的增量的3分之1再加1。但是无论如何，最后一次预排序的增量必须为1，这样才能对序列进行完全的排序。

前面只提到了预排序却没提到预排序的排序方法是什么，实际上预排序采用的排序算法是插入排序的变种之一。插入排序是比较前一个数据，而希尔排序中的预排序是比较前增量个数据。

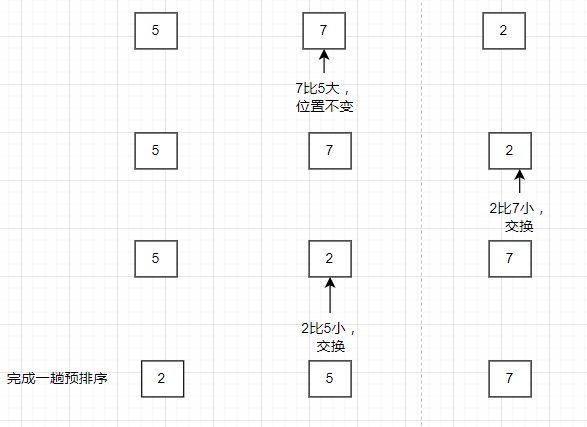
每完成一趟预排序，序列更加接近有序。与此同时逐渐减少预排序的增量，让预排序能让序列更加有序。最后一趟希尔排序增量一定要为1，此时整个序列变得有序。

这里先给出希尔排序的程序，再图解过程

void ShellSort(int* a, int n)//n是数组的元素个数
{
	int gap = n;//增量为gap
	int tmp = 0;
	while (gap > 1)
	{
		gap /= 2;//一趟希尔排序后增量变化，保证最后一趟希尔排序的增量为1.
		//也可以写成，gap=gap/3+1，各有优劣
		for (int i = 0; i < n - gap; i++)//一趟预排序
		{
			int end = i;
			while (end >= 0)
			{
				tmp = a[end + gap];
				if (a[end] > a[end + gap])
				{
					a[end + gap] = a[end];//将预排的子序列进行排序
					end -= gap;
				}
				else
				{
					break;
				}
				a[end + gap] = tmp;//插入合适的数据位置
			}
		}
	}
}

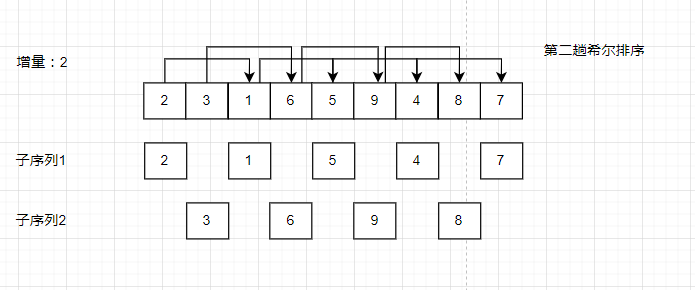
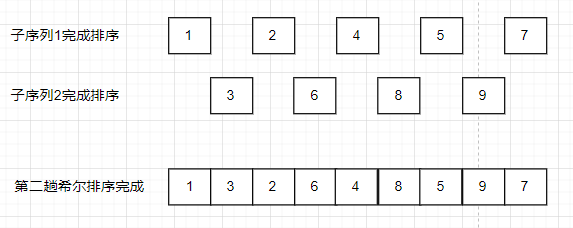
可以发现经过两趟排序之后，序列基本有序

我们对比一下增量为1的希尔排序和插入排序的代码
插入排序的代码：

for (int i = 1; i < n ; i++)
{
	end = i;//从第2个数据开始插入排序，一直到第n个数，构成排序
	int tmp = a[end];//将进行插入排序的数据进行保存，方便找到位置后进行插入
	while (end > 0)
	{
		if (tmp < a[end - 1])
		{
			a[end] = a[end - 1];//将不符合条件的数据向后移动一位，空出空间。
			end--;//继续往前比较
		}
		else//找到适合的位置就退出循环，此时end位于合适的位置
		{
			break;
		}
	}
	a[end] = tmp;
}

增量为1的希尔排序的代码

for (int i = 0; i < n - gap; i++)//一趟预排序
{
	int end = i;
	while (end >= 0)
	{
		tmp = a[end + gap];
		if (a[end] > a[end + gap])
		{
			a[end + gap] = a[end];//将预排的子序列进行排序
			end -= gap;
		}
		else
		{
			break;
		}
		a[end + gap] = tmp;//插入合适的数据位置
	}
}

将希尔排序的增量（gap）改为1，可以发现与插入排序的代码逻辑无异。