系列文章
Svg Flow Editor 原生svg流程图编辑器(一)
Svg Flow Editor 原生svg流程图编辑器(二)
Svg Flow Editor 原生svg流程图编辑器(三)
Svg Flow Editor 原生svg流程图编辑器(四)
实现Echart统计图
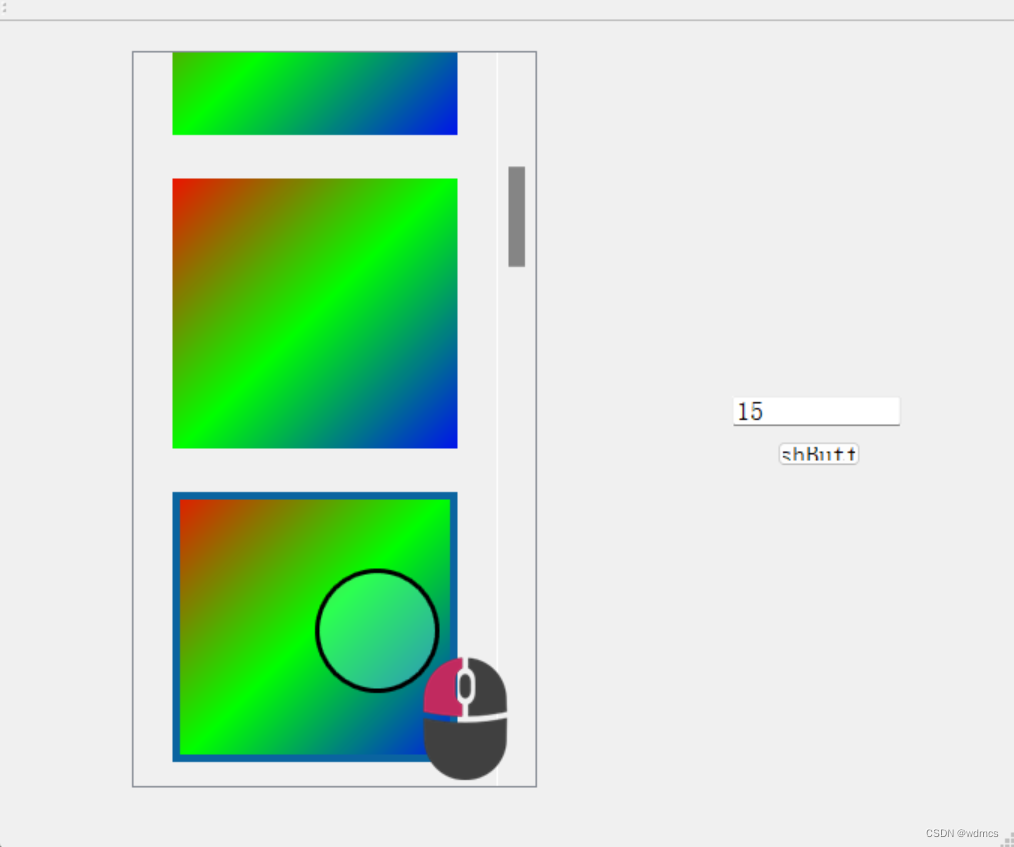
统计图的底层我们采用apache echarts 实现【Apache ECharts】,先封装GEchart,GEchart是我们的外层框架,支持形变、旋转,与Rect等svg元件类似的结构,但是内部是div实现:

同时,样式设置上与svg还是有些不同,需要单独处理下。
/**
* 需要向外暴露 setOption 方法,供数据变化后重新渲染
* @param option
*/
private setOption() {
if (!this.option) throw new Error(messageInfo.optionError);
this.myChart.setOption(this.option);
return this;
}
/**
* 向外提供 update 方法,供用户在 option 变化后更新页面内容
* 因 option 是引用地址,因此 可以不需要传递参数,从而实现数据更新
* @returns
*/
public update() {
return this.setOption();
}事件上,则是核心的 setOption 与 update 两个方法,update则是向外提供给用户更新时使用。同时,缩放会导致父节点尺寸变化,因此还需要监听尺寸变化实现动态Echart重绘,使用第三方库实现此功能【也可以使用 const ob = new ResizeObserver() 这个原生API实现哈,看自己的需求】:
import elementResizeDetectorMaker from "element-resize-detector";
var erd = elementResizeDetectorMaker();
// 监听元素尺寸变化,重新渲染echart 使得宽高自适应
erd.listenTo(this.div, () => this.myChart.resize());还需要封装一层插件,因为GEchart是核心类,不能直接提供给用户,也不便于结构管理:
// echarts 插件 多一层的原因是构建新的实例
export class SEchart {
private draw: Draw;
constructor(draw: Draw) {
this.draw = draw;
}
/**
* 初始化 Echart
* @param option
* @returns
*/
public init(option: object) {
return new GEchart(this.draw, option);
}
}
// 关键!需要注册插件,提供 echart 绘制能力
const echart = editor.plugin("echart");
// 初始化echart
const line = echart?.init(option);
// 模拟数据更新
setTimeout(() => {
data[0] = "123123mode";
line?.update();
}, 1000);

注意哈,class GEchart extends GraphCommon, GEchart 类继承了 Common 类,拥有元件的所有属性方法,包括 setWidth position 等;而 SEchart 则是隔离用户触碰核心类,同时也给用户注册多实例提供可能,也是对插件化提供支持。
Echart 的事件处理,则是基于EventBus 实现实例的 emit on 操作:
this.event = new EventBus();
// Echarts click
this.myChart.on("click", (params: object) =>
this.event.emit("click", params)
);
// Echarts 鼠标移出
this.myChart.on("mouseout", (params: object) =>
this.event.emit("mouseout", params)
);
// Echarts 鼠标移入
this.myChart.on("mouseover", (params: object) =>
this.event.emit("mouseover", params)
);
const echart = editor.plugin('echart')
const bar=echart.init(barOption)
bar.event.on('click',p=>{
// p 是回调的参数
})直角折线
以下实现思路参考logicFlow直角折线思想,连接锚点mousedown事件中,我们要记录当前锚点的位置信息:
// 1. 获取当前元素的宽高位置信息
const width = graph.getWidth();
const height = graph.getHeight();
const x = graph.getX();
const y = graph.getY();
// 2. 需要计算起点位置 -- 锚点位置受padding影响
const typeMap: { [key: string]: { sx: number; sy: number } } = {
"0": { sx: x, sy: y + height / 2 },
"1": { sx: x + width / 2, sy: y },
"2": { sx: x + width, sy: y + height / 2 },
"3": { sx: x + width / 2, sy: y + height },
};
const sx = typeMap[type].sx + 10;
const sy = typeMap[type].sy + 10;使用editorBox来接收mousemove事件以实现流程的拖动,但是在拖动过程中,可能会经过多个元素,导致 offset 值得变化,需要做优化:
/**
* 需要做位置矫正
* class='sf-editor-box-graphs' 正确
* class='sf-editor-box-graphs-main' 异常 偏移量加 offsetLeft offsetTop 值
* class='' 异常
*/ 
绘制结束后,需要根据logicFlow的思想,构建出下面这个图形:
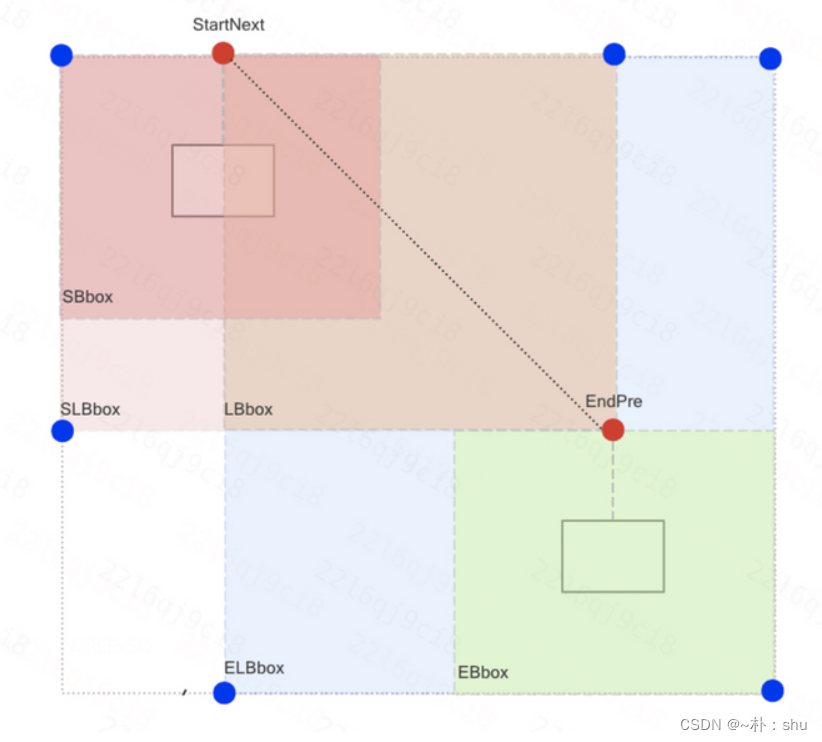
实现的思路是根据线的起点、终点关联的元件计算得出:

实现关键代码:
console.log("### 绘制最终折线,根据框的宽高位置信息获取基础数据");
const eid = this.line.getAttribute("eid") as string;
const sid = this.line.getAttribute("sid") as string;
if (!eid) return this.lineBox.remove();
// 不然处理折线的寻径算法
this.line.setAttribute("stroke-dasharray", "");
// 1. 获取 sid eid 构建 graph
const Sgraph = new Graph(this.draw, sid);
const Egraph = new Graph(this.draw, eid);
// 2. 获取start的宽高 位置信息
const sx = Sgraph.getX();
const sy = Sgraph.getY();
// 3. 获取 end 的宽高 位置信息
const ex = Egraph.getX();
const ey = Egraph.getY();
// 4. 需要知道哪个元件在最后 也就是 graph x 最大
const maxGrapg = sx > ex ? Sgraph : Egraph;
// 5. 构建 OFFSET 的矩形 --- 受padding的影响
const lx = Math.min(sx, ex) - OFFSET + 10;
const ly = Math.min(sy, ey) - OFFSET + 10;
this.setX(lx);
this.setY(ly);
this.lineBox.style.backgroundColor = "rgba(0,0,0,0.1)";
// 6. 取消直线
this.line.setAttribute("points", "");
// 7. 设置宽高
const mw = maxGrapg.getWidth();
const mh = maxGrapg.getHeight();
const mx = maxGrapg.getX();
const my = maxGrapg.getY();
// 自此,整个线的宽高= lx -> mx + mw + OFFSET
const lw = mx - lx + mw + OFFSET + 10;
const lh = my - ly + mh + OFFSET + 10;
this.setWidth(lw);
this.setHeight(lh);
根据矩形框,找出所有可能路径关键点:
// 做点的纠正-因为 计算得到的是 基于背景的 而线的绘制基于新的 div 坐标,需要做处理 【并且受 padding 的影响】
const getX = (x: number) => x - lx + 10;
const getY = (y: number) => y - ly + 10;
// 起点
const startType = typeMap[st]({ x: sx, y: sy, w: sw, h: sh });
const startPoint = { x: getX(startType.x), y: getY(startType.y) };
points.push(startPoint);
// 终点
const endType = typeMap[et]({ x: ex, y: ey, w: ew, h: eh });
const endPoint = { x: getX(endType.x), y: getY(endType.y) };
points.push(endPoint);
// 如果存在间隙,则取偏移量的点,如果不存在间隙,则不取偏移量的点
const intervalX = maxGrapg.getX() - minGraph.getX() + minGraph.getWidth();
const intervalY = maxGrapg.getY() - minGraph.getY() + minGraph.getHeight();
if (intervalX > OFFSET && intervalY > OFFSET) {
// 取偏移量
const startOffsetPoint = { x: getX(startType.ox), y: getY(startType.oy) };
points.push(startOffsetPoint);
const endOffsetPoint = { x: getX(endType.ox), y: getY(endType.oy) };
points.push(endOffsetPoint);
}轴线与边界的交点:
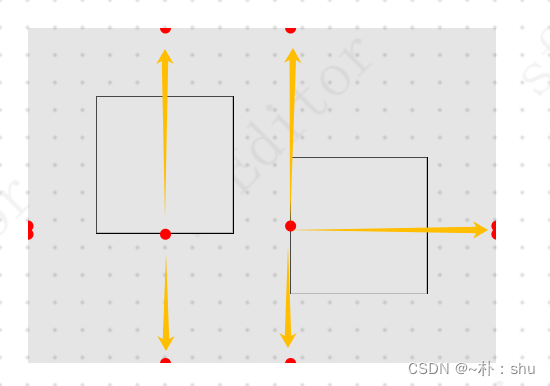
A* 算法实现:
const list: expandP[] = JSON.parse(JSON.stringify(points)); // 深拷贝简单实现
var optimal: expandP[] = []; // 记录最优解
// 计算当前点的最短路径
const computedDistance = (p: expandP) => {
console.group("开始 A* 算法");
console.log("当前点", p);
// 获取list中 x、y 相同的点,并计算最短路径
const ps = list.filter((i: expandP) => i.x === p.x || i.y === p.y);
// 循环当前可达的点,并计算距离
ps.forEach((i: expandP) => {
i.d = Infinity; // 默认无穷大
// 并且计算传入的点与当前点的向量是否穿过矩形
// 计算曼哈顿距离
i.d = Math.abs(i.x - endPoint.x) + Math.abs(i.y - endPoint.y);
});
ps.sort((a, b) => (a.d as number) - (b.d as number));
console.log("当前可达的点", ps);
this.drawPoint(ps[0], "green");
console.groupEnd();
return ps[0];
};
/**
* 【开始寻径算法】
* 1. 找到当前点的 x y 相同的点作为可达点,
* 2. 并且规定,当前点的可达距离为1,取到终点的曼哈顿距离
* 3. 还需要判断当前两点的向量是否穿过矩形
*/
const search = () => {
const point = optimal.length ? optimal[optimal.length - 1] : startPoint; // 当前的最优解
if (point.x === endPoint.x && point.y === endPoint.y)
return console.log("A* 算法结束,最优路径为 => ", optimal);
const optimalPoint = computedDistance(point);
optimal.push(optimalPoint);
};
这样会穿过元件,不符合,因此需要使用处理计算,判断是否穿过节点本身:
// 检查两个点组成的线段是否穿过起终点元素
private checkLineThroughElements(p1: p, p2: p) {
let rects = [this.Sgraph, this.Egraph];
let minX = Math.min(p1.x, p2.x);
let maxX = Math.max(p1.x, p2.x);
let minY = Math.min(p1.y, p2.y);
let maxY = Math.max(p1.y, p2.y);
// 水平线
if (p1.y === p2.y) {
for (let i = 0; i < rects.length; i++) {
let rect = rects[i];
if (
minY > rect.getY() - this.ly &&
minY < rect.getY() + rect.getHeight() - this.ly &&
minX < rect.getX() + rect.getWidth() - this.lx &&
maxX > rect.getX() - this.lx
) {
return true;
}
}
} else if (p1.x === p2.x) {
// 垂直线
for (let i = 0; i < rects.length; i++) {
let rect = rects[i];
if (
minX > rect.getX() - this.lx &&
minX < rect.getX() + rect.getWidth() - this.lx &&
minY < rect.getY() + rect.getHeight() - this.ly &&
maxY > rect.getY() - this.ly
) {
return true;
}
}
}
return false;
}推荐大家看一下该博客,我也借鉴了些思路,在点的分析,定位,算法的实现上,都看了他的代码,但是还有些部分需要根据项目实际进行优化的点。关联线探究,如何连接流程图的两个节点

最终实现效果:

这部分应该是最难的了,目前实现起来,在临界值的处理上,还是有些问题,包括距离相近时,和优化线的方向问题,还没有做兼容处理。
发布NPM
包的发布过程就不细说了,大家可以参考网上的教程,如果 npm login 报错,基本上切换淘宝镜像就可以解决问题了。目前经过 mvp 版本的升级迭代,基本具备流程图的绘制、交互功能,我们发布 1.0 版本,主要是测试应用功能模块是否正常。【worker 路径存在问题,目前版本使用同步实现,后续优化】
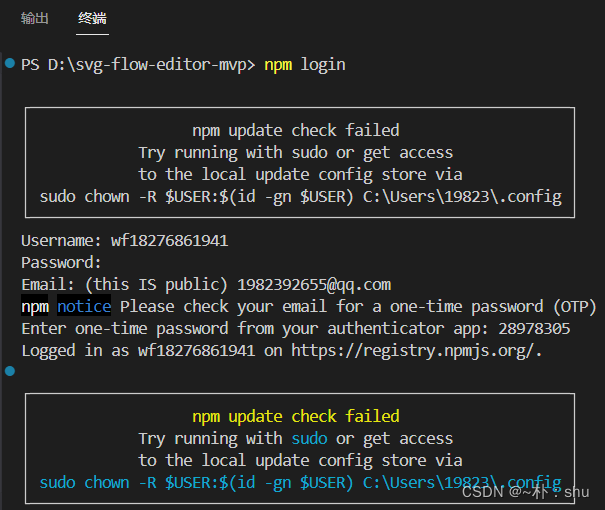
当你升级版本的时候报错,一定需要全部提交代码,才可以进行升级:
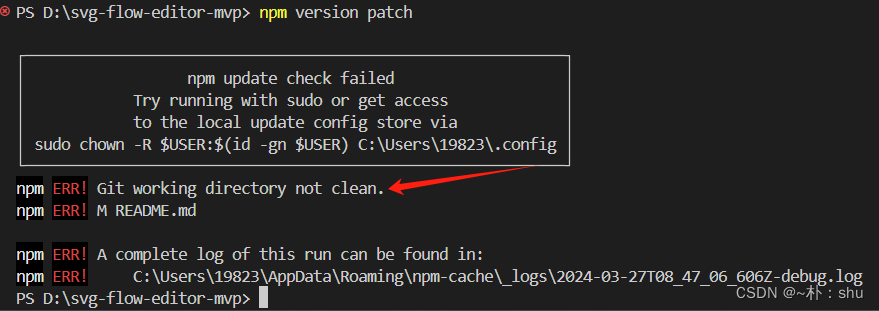
 版本升级成功,可以在 npm 官网进行查看:
版本升级成功,可以在 npm 官网进行查看:

新建空项目,进行测试:


使用过程中,发现有些静态资源请求地址有问题,我们采取base64编码的方式处理,不走请求,即可解决该问题,整体效果如下:
总结
目前已经基本实现流程图的图形绘制、自定义icon 、文本输入,剩余的优化问题包括:
1. 折线算法优化;
2. 元件库拓展;
3. 顶部菜单栏及相应 command API开发;
4. 快捷键的完善与相应功能实现。
大家可以下载包试试,有啥问题随时反馈改进哦。
npm i svg-flow-editor-mvp