蓝桥杯java组最少砝码

news2024/9/25 7:15:19

问题描述】

你有一架天平。现在你要设计一套砝码，使得利用这些砝码可以称出任意小于等于 N 的正整数重量。
那么这套砝码最少需要包含多少个砝码？
注意砝码可以放在天平两边。

【输入格式】
输入包含一个正整数 N。

【输出格式】
输出一个整数代表答案。

【样例输入】
7

【样例输出】
3

【样例说明】
3 个砝码重量是 1、4、6，可以称出 1 至 7 的所有重量。
1 = 1；
2 = 6 − 4 (天平一边放 6，另一边放 4)；
3 = 4 − 1；
4 = 4；
5 = 6 − 1；
6 = 6；
7 = 1 + 6；
少于 3 个砝码不可能称出 1 至 7 的所有重量。

代码

import java.util.Scanner;  
  
/**  
 * @author Fancier  
 * @version 1.0  
 * @description: TODO  
 * @date 2024/3/27 14:20  
 */  
public class Main {  
    public static void main(String[] args) {  
        int n = new Scanner(System.in).nextInt();    
        int maxWeight = 1, minCnt = 1;  
        while (maxWeight < n) {  
            maxWeight = maxWeight * 3 + 1;  
            minCnt++;  
        }  
        System.out.println(minCnt);  
    }  
}

题解

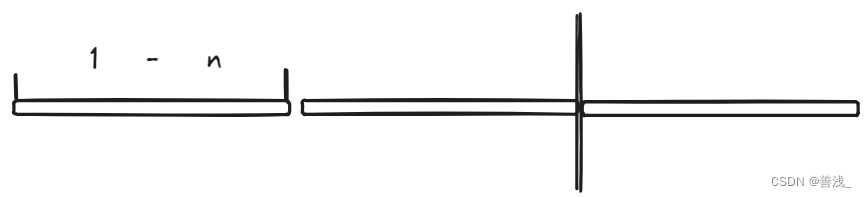
如果我们可以控制的区间范围是 [1, n] 最少砝码为x个
此时我们想扩大区间范围就只可以增加砝码
假设增加的砝码重量为 k
因为我们可以控制 [1, n] 的重量, 而且因为可以把砝码放在左右两把, 想当于我们可以进行加减操作
所以新增砝码后, 我们又可以控制[k - n, k + n] 的区间范围了

让这个新增的控制范围与我们原来的可以控制的范围相邻, 就得到了最大的可控范围

另 n + 1 = k - n k = 2n + 1
那么x + 1可以控制的最范围就是[1, 3n + 1]
在这里插入图片描述