封建迷信我嗤之以鼻，财神殿前我长跪不起
一、二叉树链式结构的实现
1.二叉树的创建
1.1 手动创建
1.2 前序递归创建
2.二叉树的遍历
2.1 前序，中序以及后序遍历概念
2.2 层序遍历概念
2.3 前序打印实现
2.4 中序打印实现
2.4 后序打印实现
2.5 层序打印实现
2.6 判断是否为完全二叉树
3. 其他功能实现
3.1 二叉树节点个数
3.2 二叉树第k层节点个数
3.3 二叉树查找值为x的节点
3.4 二叉树叶子节点个数
3.5 二叉树的销毁
二、完结撒❀
–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀-正文开始-❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–
一、二叉树链式结构的实现
再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：
1. 空树。
2. 非空：根节点，根节点的左子树、根节点的右子树组成的。
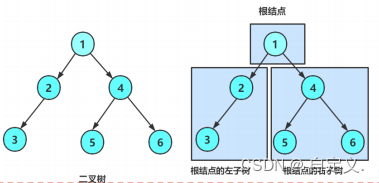
从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。
1.二叉树的创建
二叉树节点链式结构：
//对二叉树的使用链式结构（非满二叉树，非完全二叉树）
typedef int BTDataType;
typedef struct BinTreeNode
{
struct BinTreeNode* left;
struct BinTreeNode* right;
BTDataType val;
}BTNode;
1.1 手动创建
我们在一些情况下为了方便理解二叉树，我们会直接按照二叉树逻辑进行手动创建，这样更容易让人理解
代码实现：
//手搓一个二叉树
BTNode* BuyBTNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
return;
}
newnode->left = NULL;
newnode->right = NULL;
newnode->val = x;
return newnode;
}
BTNode* CreateTree()
{
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
return n1;
}
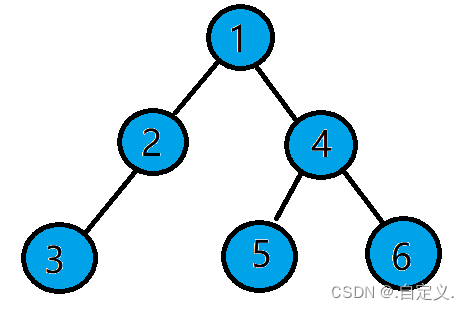
按照上面代码为例，实现的二叉树为：
1.2 前序递归创建
不清楚前序的同学可以先学习下面二叉树的遍历，再上来进行学习。
二叉树分为根，左子树，右子树，而左子树，右子树又可以分为根和左子树右子树（当然左右子树也可以为空），那么这就很符合递归的逻辑，所以我们要完成前序递归创建二叉树就需要先知道：
1.递归子问题（每次递归所要执行的操作）
2.最小子问题（终止递归返回条件）
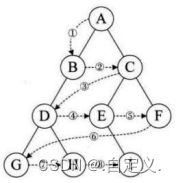
比如我们要前序递归创建下面二叉树：
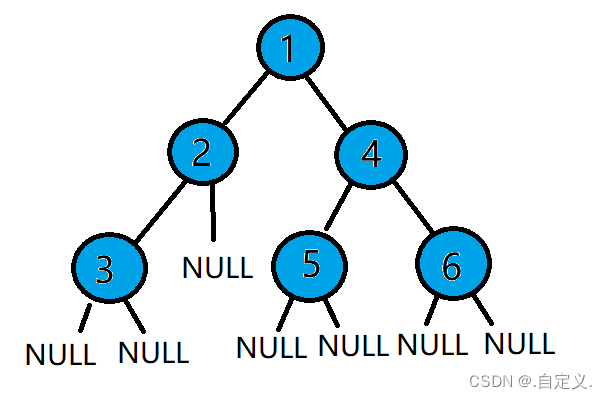
其前序遍历为：1 2 3 4 5 6
代码实现：
//创建一个二叉树（按照前序创建）
BTNode* BTCreate(BTNode* root)
{
BTDataType ret = 0;
printf("请输入该节点的值:>");
scanf("%d", &ret);
if (ret != 0)//设置结束链表创建点
{
root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
return;
}
root->val = ret;
root->left = NULL;
root->right = NULL;
root->left = BTCreate(root->left);
root->right = BTCreate(root->right);
}
return root;
}
根据代码输入：1 2 3 0 0 0 4 5 0 0 6 0 0
即可创建上面二叉树
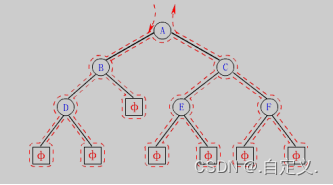
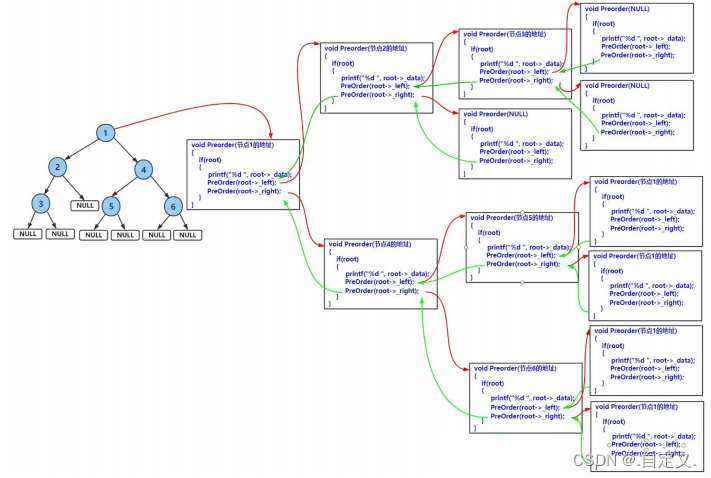
递归代码导图：
比较抽象，大家理解就行
中序和后序大家感兴趣可以下去查阅学习。
2. 二叉树的遍历
2.1 前序，中序以及后序遍历概念
学习二叉树结构，最简单的方式就是遍历。
所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。
访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。（N，L，R）
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。（L，N，R）
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。（L，R，N）
由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
下面主要分析前序递归遍历，中序与后序图解类似，同学们可自己动手绘制。
我们以下面二叉树为例：
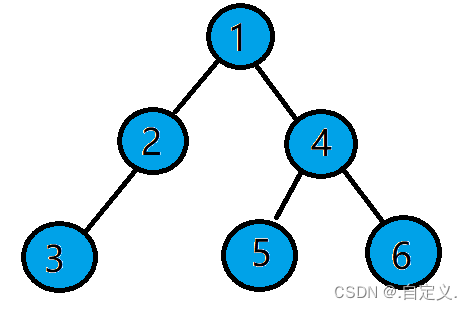
前序遍历递归图解：
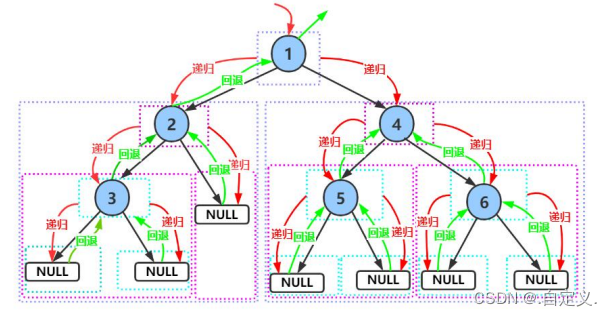
前序遍历结果：1 2 3 4 5 6
中序遍历结果：3 2 1 5 4 6
后序遍历结果：3 2 5 6 4 1
2.2 层序遍历概念
层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
2.3 前序打印实现
根据递归先打印出根节点，再递归到左子树，再打印出左子树的根节点，继续递归到左子树直到左子树为空指针，那么函数将会继续执行当前二叉树的右子树进行递归遍历，直到为空节点。
代码实现：
//前序 根 左 右
void PreOrder(BTNode* root)
{
if(root)
{
printf("%d ", root->val);
PreOrder(root->left);
PreOrder(root->right);
}
}
前序遍历递归图解：
2.4 中序打印实现
根据递归先递归到最左边第一个叶节点，再打印出其值，从左边第一个叶节点继续往右进行递归直到空节点函数回溯到上一个递归函数，再递归到右子树，直到完成整个二叉树的中序递归遍历
代码实现：
//中序 左 根 右
void InOrder(BTNode* root)
{
if(root)
{
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}
}
中序遍历递归图解：
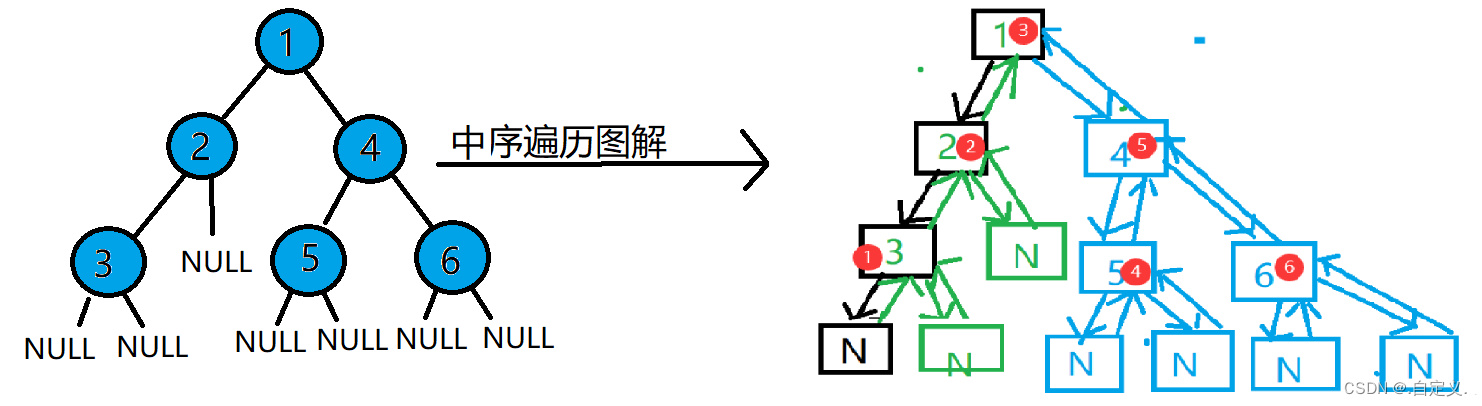
序号表示打印循序，先从黑色箭头递归下去，再从绿色箭头回溯上来，再到蓝色箭头。
2.4 后序打印实现
先递归到最左边第一个叶节点，直到递归到空节点再回溯到上一节点的右节点继续递归直到空节点，回溯到上一节点进行打印，再回溯到上一节点的右节点，继续递归直到遇到空节点回溯。
代码实现:
//后序 左 右 根
void PostOrder(BTNode* root)
{
if (root)
{
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}
}
后序遍历递归图解：
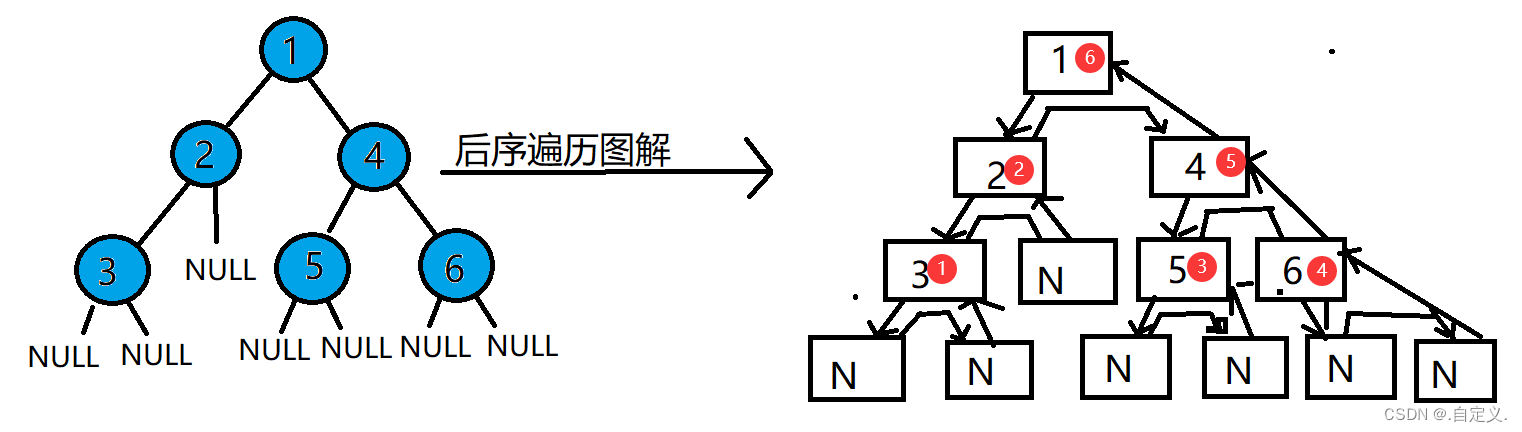序号表示打印顺序。
2.5 层序打印实现
层序打印实现需要用到队列。
实现逻辑：
从二叉树的根开始向队列中进行存储，根存储完毕后将根出队列的同时将两个左右孩子节点也存到队列当中，之后在对左孩子节点进行出队列得同时将左孩子节点的左右孩子节点存都队列中（为空不进行存储），再继续向后将右孩子出队列得同时再将右孩子得左右孩子存入队列中，以此入队列，出队列，直到队列为空为止，输出变为层序。
实现逻辑图解：
代码实现：
void TreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->val);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestroy(&q);
}
对应队列函数可以去我得博客：栈和队列进行查找学习。
2.6 判断是否为完全二叉树
实现这个功能也用到了队列，所以我们放这里进行讲解
代码实现：
//判断是否为完全二叉树
bool TreeIsComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
return false;
}
}
QueueDestroy(&q);
return true;
}
判断逻辑：
这个判断逻辑很简单，我们可以再回顾一下完全二叉树的概念：
完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
我们直接按照上面教的对二叉树进行层序遍历，当遇到空节点直接跳出第一次while循环，如果是完全二叉树那么队列中后面存储的将都为空节点，如果不是完全二叉树，那么队列中将还存有非空间点。
所以跳出第一次循环后我们判断队列中是否还有非空节点即可，若有返回fasle，若没有返回true。
3.其他功能实现
3.1 二叉树节点个数
代码实现：
//查节点数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
同样运用递归实现
其递归图解为：
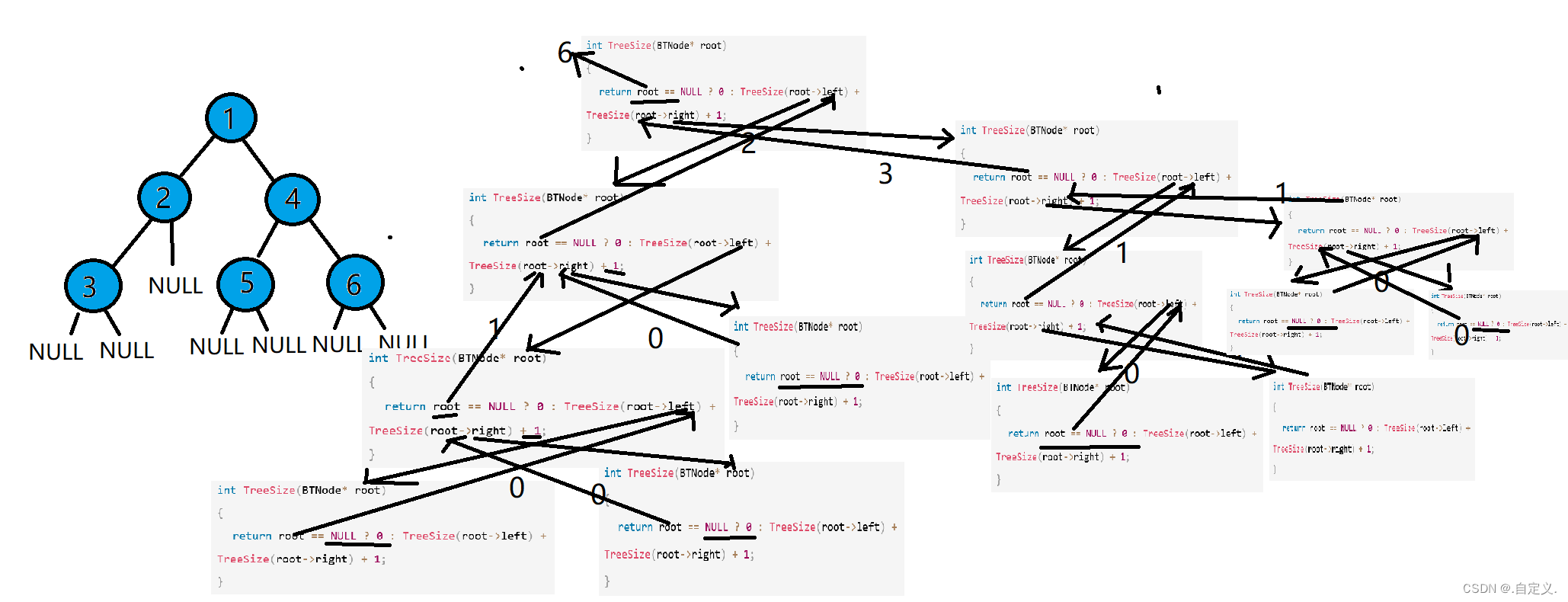大家可以跟随箭头走一遍逻辑。（我知道画的不好qaq，大家将就理解一下逻辑即可）
3.2 二叉树第k层节点个数
代码实现：
//计算第k行的节点数
int TreeKLevel(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)//必须先判断这个
{
return 0;
}
if (k == 1)//在判断这个
{
return 1;
}
return TreeKLevel(root->left, k-1)+TreeKLevel(root->right, k-1);
}
递归图解大家可以尝试画一下，有助于大家理解递归。
实现逻辑手工绘图：
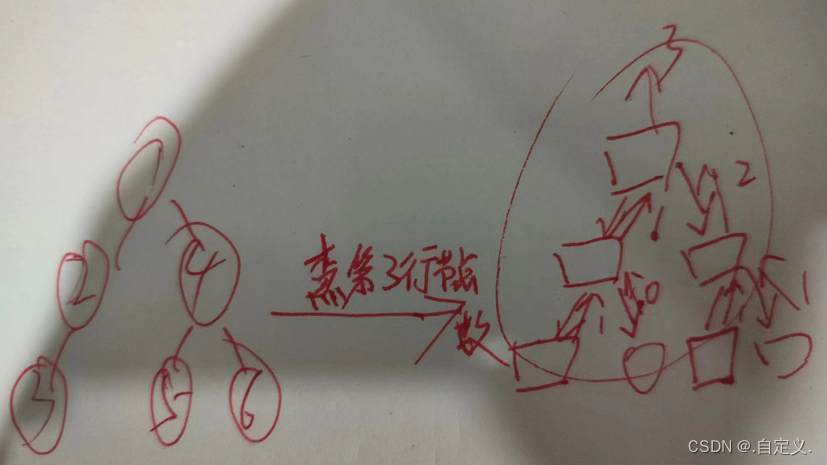
3.3 二叉树查找值为x的节点
代码实现：
//查找x所在的节点返回对应指针
BTNode* TreeFind(BTNode* root, int x)
{
if (root == NULL)
{
return NULL;
}
if (root->val == x)
{
return root;
}
BTNode* ret1 = TreeFind(root->left,x);
if (ret1)
{
return ret1;
}
BTNode* ret2 = TreeFind(root->right,x);
if (ret2)
{
return ret2;
}
return NULL;
}
实现逻辑手工绘图：
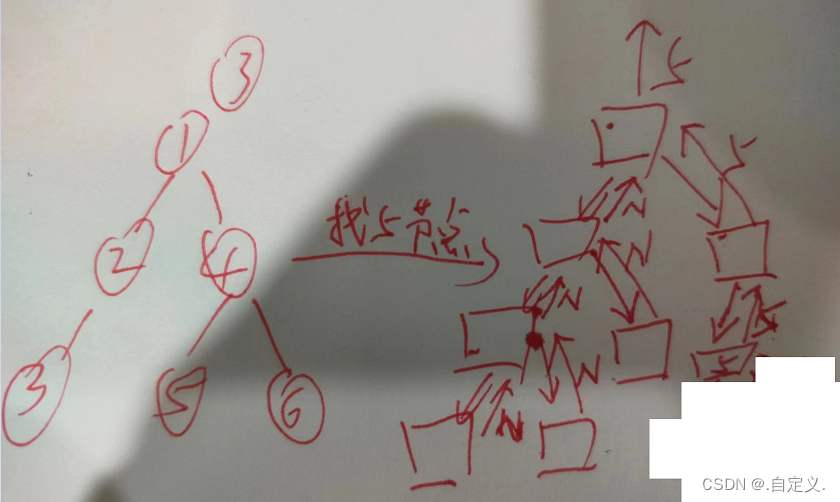
3.4 二叉树叶子节点个数
代码实现：
// 二叉树叶子节点个数
int BTLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BTLeafSize(root->left) + BTLeafSize(root->right);
}
3.5 二叉树的销毁
代码实现：
//二叉树销毁
void TreeDestroy(BTNode* root)//一级指针root在该函数内置为空指针无效
{
if (root == NULL)
{
return;
}
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
//root = NULL,需要在函数外置为空指针
}
二、完结撒❀
如果以上内容对你有帮助不妨点赞支持一下，以后还会分享更多编程知识，我们一起进步。
最后我想讲的是，据说点赞的都能找到漂亮女朋友❤
