LeetCode 每日一题 Day 109-115

news2024/9/27 21:21:13

1969. 数组元素的最小非零乘积

给你一个正整数 p 。你有一个下标从 1 开始的数组 nums ，这个数组包含范围 [1, 2p - 1] 内所有整数的二进制形式（两端都 包含）。你可以进行以下操作 任意 次：

从 nums 中选择两个元素 x 和 y 。
选择 x 中的一位与 y 对应位置的位交换。对应位置指的是两个整数 相同位置 的二进制位。
比方说，如果 x = 1101 且 y = 0011 ，交换右边数起第 2 位后，我们得到 x = 1111 和 y = 0001 。

请你算出进行以上操作 任意次 以后，nums 能得到的 最小非零 乘积。将乘积对 109 + 7 取余 后返回。

注意：答案应为取余 之前 的最小值。

示例 1：

输入：p = 1
输出：1
解释：nums = [1] 。
只有一个元素，所以乘积为该元素。

示例 2：

输入：p = 2
输出：6
解释：nums = [01, 10, 11] 。
所有交换要么使乘积变为 0 ，要么乘积与初始乘积相同。
所以，数组乘积 1 * 2 * 3 = 6 已经是最小值。

示例 3：

输入：p = 3
输出：1512
解释：nums = [001, 010, 011, 100, 101, 110, 111]

  • 第一次操作中，我们交换第二个和第五个元素最左边的数位。
    • 结果数组为 [001, 110, 011, 100, 001, 110, 111] 。
  • 第二次操作中，我们交换第三个和第四个元素中间的数位。
    • 结果数组为 [001, 110, 001, 110, 001, 110, 111] 。
      数组乘积 1 * 6 * 1 * 6 * 1 * 6 * 7 = 1512 是最小乘积。

提示：

1 <= p <= 60

贪心+快速幂:

class Solution {
    const int mod = 1'000'000'007;

    long long pow(long long x, int p) {
        x %= mod;
        long long res = 1;
        while (p--) {
            res = res * x % mod;
            x = x * x % mod;
        }
        return res;
    }

public:
    int minNonZeroProduct(int p) {
        long long k = (1LL << p) - 1;
        return k % mod * pow(k - 1, p - 1) % mod;
    }
};

(偷看灵神题解

2671. 频率跟踪器

请你设计并实现一个能够对其中的值进行跟踪的数据结构，并支持对频率相关查询进行应答。

实现 FrequencyTracker 类：

FrequencyTracker()：使用一个空数组初始化 FrequencyTracker 对象。
void add(int number)：添加一个 number 到数据结构中。
void deleteOne(int number)：从数据结构中删除一个 number 。数据结构 可能不包含 number ，在这种情况下不删除任何内容。
bool hasFrequency(int frequency): 如果数据结构中存在出现 frequency 次的数字，则返回 true，否则返回 false。

示例 1：

输入
[“FrequencyTracker”, “add”, “add”, “hasFrequency”]
[[], [3], [3], [2]]
输出
[null, null, null, true]

解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.add(3); // 数据结构现在包含 [3]
frequencyTracker.add(3); // 数据结构现在包含 [3, 3]
frequencyTracker.hasFrequency(2); // 返回 true ，因为 3 出现 2 次
示例 2：

输入
[“FrequencyTracker”, “add”, “deleteOne”, “hasFrequency”]
[[], [1], [1], [1]]
输出
[null, null, null, false]

解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.add(1); // 数据结构现在包含 [1]
frequencyTracker.deleteOne(1); // 数据结构现在为空 []
frequencyTracker.hasFrequency(1); // 返回 false ，因为数据结构为空
示例 3：

输入
[“FrequencyTracker”, “hasFrequency”, “add”, “hasFrequency”]
[[], [2], [3], [1]]
输出
[null, false, null, true]

解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.hasFrequency(2); // 返回 false ，因为数据结构为空
frequencyTracker.add(3); // 数据结构现在包含 [3]
frequencyTracker.hasFrequency(1); // 返回 true ，因为 3 出现 1 次

提示：

1 <= number <= 1e5
1 <= frequency <= 1e5
最多调用 add、deleteOne 和 hasFrequency 共计 2 * 1e5 次

双哈希：

class FrequencyTracker {
public:
    unordered_map<int, int> numToFreq;
    unordered_map<int, unordered_set<int>> freqToNums;

    FrequencyTracker() {}

    void add(int number) {
        if (numToFreq[number]) {
            freqToNums[numToFreq[number]].erase(number);
            if (freqToNums[numToFreq[number]].empty()) {
                freqToNums.erase(numToFreq[number]);
            }
        }
        numToFreq[number]++;
        freqToNums[numToFreq[number]].insert(number);
    }

    void deleteOne(int number) {
        if (numToFreq[number]) {
            freqToNums[numToFreq[number]].erase(number);
            if (freqToNums[numToFreq[number]].empty()) {
                freqToNums.erase(numToFreq[number]);
            }
            numToFreq[number]--;
            if (numToFreq[number]) {
                freqToNums[numToFreq[number]].insert(number);
            } else {
                numToFreq.erase(number);
            }
        }
    }

    bool hasFrequency(int frequency) { return freqToNums.count(frequency); }
};

/**
 * Your FrequencyTracker object will be instantiated and called as such:
 * FrequencyTracker* obj = new FrequencyTracker();
 * obj->add(number);
 * obj->deleteOne(number);
 * bool param_3 = obj->hasFrequency(frequency);
 */

2617. 网格图中最少访问的格子数(Hard)

给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。

当你在格子 (i, j) 的时候，你可以移动到以下格子之一：

满足 j < k <= grid[i][j] + j 的格子 (i, k) （向右移动），或者
满足 i < k <= grid[i][j] + i 的格子 (k, j) （向下移动）。
请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数，如果无法到达右下角格子，请你返回 -1 。

示例 1：

在这里插入图片描述

输入：grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]
输出：4
解释：上图展示了到达右下角格子经过的 4 个格子。

示例 2：

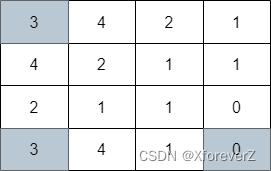
在这里插入图片描述

输入：grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]
输出：3
解释：上图展示了到达右下角格子经过的 3 个格子。

示例 3：

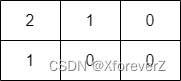
在这里插入图片描述

输入：grid = [[2,1,0],[1,0,0]]
输出：-1
解释：无法到达右下角格子。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 1e5
1 <= m * n <= 1e5
0 <= grid[i][j] < m * n
grid[m - 1][n - 1] == 0

菜鸡不会抄了灵神题解，单调栈dp：

class Solution {
public:
    int minimumVisitedCells(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size(), mn;
        vector<vector<pair<int, int>>> col_stacks(n); // 每列的单调栈
        vector<pair<int, int>> row_st;                // 行单调栈
        for (int i = m - 1; i >= 0; i--) {
            row_st.clear();
            for (int j = n - 1; j >= 0; j--) {
                int g = grid[i][j];
                auto& col_st = col_stacks[j];
                mn = i < m - 1 || j < n - 1 ? INT_MAX : 1;
                if (g) { // 可以向右/向下跳
                    // 在单调栈上二分查找最优转移来源
                    auto it = lower_bound(row_st.begin(), row_st.end(), j + g,
                                          [](const auto& a, const int b) {
                                              return a.second > b;
                                          });
                    if (it < row_st.end())
                        mn = it->first + 1;
                    it = lower_bound(col_st.begin(), col_st.end(), i + g,
                                     [](const auto& a, const int b) {
                                         return a.second > b;
                                     });
                    if (it < col_st.end())
                        mn = min(mn, it->first + 1);
                }
                if (mn < INT_MAX) {
                    // 插入单调栈
                    while (!row_st.empty() && mn <= row_st.back().first) {
                        row_st.pop_back();
                    }
                    row_st.emplace_back(mn, j);
                    while (!col_st.empty() && mn <= col_st.back().first) {
                        col_st.pop_back();
                    }
                    col_st.emplace_back(mn, i);
                }
            }
        }
        return mn < INT_MAX ? mn : -1; // 最后一个算出的 mn 就是 f[0][0]
    }
};

题解：两种方法：单调栈优化 DP / 贪心+最小堆

2549. 统计桌面上的不同数字

多带几组数据，一行解决：

class Solution {
public:
    int distinctIntegers(int n) { return max(n - 1, 1); }
};

322. 零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1
示例 2：

输入：coins = [2], amount = 3
输出：-1
示例 3：

输入：coins = [1], amount = 0
输出：0

提示：

1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 1e4

经典DP：

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount + 1, amount + 1);
        dp[0] = 0;
        for (int i = 0; i <= amount; i++) {
            for (int coin : coins) {
                if (coin <= i) {
                    dp[i] = min(dp[i], dp[i - coin] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
};

518. 零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。
示例 3：

输入：amount = 10, coins = [10]
输出：1

提示：

1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins 中的所有值 互不相同
0 <= amount <= 5000

动态规划背包问题，与上一题类似：

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount + 1);
        dp[0] = 1;
        for (int coin : coins) {
            for (int i = coin; i <= amount; i++) {
                dp[i] += dp[i - coin];
            }
        }
        return dp[amount];
    }
};

2642. 设计可以求最短路径的图类（Hard)

给你一个有 n 个节点的 有向带权 图，节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示，其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。

请你实现一个 Graph 类：

Graph(int n, int[][] edges) 初始化图有 n 个节点，并输入初始边。
addEdge(int[] edge) 向边集中添加一条边，其中 edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。
int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径 最小 代价。如果路径不存在，返回 -1 。一条路径的代价是路径中所有边代价之和。

示例 1：

输入：
[“Graph”, “shortestPath”, “shortestPath”, “addEdge”, “shortestPath”]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
输出：
[null, 6, -1, null, 6]

解释：
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示：3 -> 0 -> 1 -> 2 ，总代价为 3 + 2 + 1 = 6 。
g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。
g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边，得到第二幅图。
g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ，总代价为 2 + 4 = 6 。

提示：

1 <= n <= 100
0 <= edges.length <= n * (n - 1)
edges[i].length == edge.length == 3
0 <= fromi, toi, from, to, node1, node2 <= n - 1
1 <= edgeCosti, edgeCost <= 1e6
图中任何时候都不会有重边和自环。
调用 addEdge 至多 100 次。
调用 shortestPath 至多 100 次。

dijkstra最短路：

class Graph {
public:
    static constexpr int INF = INT_MAX / 2;
    vector<vector<pair<int, int>>> g;

    Graph(int n, vector<vector<int>>& edges) {
        g.resize(n);
        for (const auto& e : edges) {
            int u = e[0], v = e[1], w = e[2];
            g[u].emplace_back(v, w);
        }
    }

    void addEdge(const vector<int>& edge) {
        int u = edge[0], v = edge[1], w = edge[2];
        g[u].emplace_back(v, w);
    }

    int shortestPath(int start, int end) {
        int n = g.size();
        vector<int> dist(n, INF);
        dist[start] = 0;
        priority_queue<pair<int, int>, vector<pair<int, int>>,
                       greater<pair<int, int>>>
            que;
        que.emplace(0, start);
        while (!que.empty()) {
            auto [d, u] = que.top();
            que.pop();
            if (d != dist[u]) {
                continue;
            }
            for (auto [v, w] : g[u]) {
                if (dist[u] + w < dist[v]) {
                    dist[v] = dist[u] + w;
                    que.emplace(dist[v], v);
                }
            }
        }
        return dist[end] == INF ? -1 : dist[end];
    }
};

/**
 * Your Graph object will be instantiated and called as such:
 * Graph* obj = new Graph(n, edges);
 * obj->addEdge(edge);
 * int param_2 = obj->shortestPath(node1,node2);
 */

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1551171.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【贫民版】Springboot导入返回错误Excel表格 ---- 通过session存储字节数据，再获取写到响应体中。

【贫民版】Springboot导入返回错误Excel表格 ---- 通过session存储字节数据，再获取写到响应体中。

目录 前言一、需求二、需求分析三、代码 前言 在开发中会遇到导入文件后&#xff0c;失败的数据需要整理在加上导入失败原因。 按照目前主流的方法&#xff0c;要么通过流输出到response响应体中&#xff0c;或者把失败的excel上传到服务器中&#xff0c;返回url让前端下载。…
阅读更多...
pyqt 创建右键菜单栏

pyqt 创建右键菜单栏

class MainModule(QMainWindow, Ui_MainWindow):def __init__(self):super().__init__(parentNone)self.setupUi(self)# 允许出现菜单栏self.tableWidget.setContextMenuPolicy(Qt.CustomContextMenu)# 对空间添加右键菜单栏处理 self.tableWidget.customContextMenuRequested.…
阅读更多...
Redis入门到实战-第十九弹

Redis入门到实战-第十九弹

Redis实战热身Count-min-sketch篇 完整命令参考官网 官网地址 声明: 由于操作系统, 版本更新等原因, 文章所列内容不一定100%复现, 还要以官方信息为准 https://redis.io/Redis概述 Redis是一个开源的&#xff08;采用BSD许可证&#xff09;&#xff0c;用作数据库、缓存、…
阅读更多...
cuDNN——核心概念

cuDNN——核心概念

在讨论graph和legacy API的细节之前&#xff0c;这一部分先介绍两者共同的核心概念。 cuDNN Handle cuDNN库暴露了一系列主机API&#xff0c;但是假设所有用到GPU的op&#xff0c;其必要的数据都可以直接从设备上访问。 使用cuDNN的应用必须先调用cudnnCreate()来初始化句柄…
阅读更多...
【C/C++】C++中的四种强制类型转换

【C/C++】C++中的四种强制类型转换

创作不易&#xff0c;本篇文章如果帮助到了你&#xff0c;还请点赞 关注支持一下♡>&#x16966;<)!! 主页专栏有更多知识&#xff0c;如有疑问欢迎大家指正讨论&#xff0c;共同进步&#xff01; &#x1f525;c系列专栏&#xff1a;C/C零基础到精通 &#x1f525; 给大…
阅读更多...
USART发送各种数据类型数据的原理及程序实现

USART发送各种数据类型数据的原理及程序实现

硬件接线&#xff1a; 显示屏的SCA接在B11&#xff0c;SCL接在B10&#xff0c;串口的RX连接A9&#xff0c;TX连接A10。 新建Serial.c和Serial.h文件 在Serial.c文件中&#xff0c;实现初始化函数&#xff0c;等需要的函数&#xff0c;首先对串口进行初始化&#xff0c;只需要…
阅读更多...
信创实力进阶，Smartbi再获华为云鲲鹏技术认证

信创实力进阶，Smartbi再获华为云鲲鹏技术认证

日前&#xff0c;经华为技术有限公司评测&#xff0c;思迈特商业智能与数据分析软件Smartbi Insight V11与华为技术有限公司Kunpeng 920 Taishan 200完成并通过相互兼容性测试认证&#xff0c;成功再获华为云鲲鹏技术认证书&#xff0c;标志着Smartbi与华为云鲲鹏产业生态合作更…
阅读更多...
http模块—http请求练习

http模块—http请求练习

题目要求&#xff1a;搭建如下http服务&#xff1a; 1.当浏览器向我们的服务器发送请求时&#xff0c;当请求类型是get请求&#xff0c;请求的url路径地址是/login。响应体结果是登录页面 2.当浏览器向我们的服务器发送请求时&#xff0c;当请求类型是get请求&#xff0c;请求…
阅读更多...
物流智能蓝牙锁控设计方案

物流智能蓝牙锁控设计方案

一、行业背景与需求分析 物流行业作为全球贸易和供应链管理的关键环节&#xff0c;其安全性和效率对整个经济体系的运作至关重要。随着电子商务的兴起和全球市场的一体化&#xff0c;物流行业正面临着前所未有的挑战&#xff0c;尤其是在货物安全、运输效率、成本控制和信息管…
阅读更多...
C#学生信息成绩管理系统

C#学生信息成绩管理系统

一、系统功能描述 本系统包括两类用户&#xff1a;学生、管理员。管理员可以通过系统来添加管理员信息、修改管理员信息、添加学生信息、修改学生信息&#xff1b;开设课程、查询课程、录入成绩、统计成绩、修改成绩、修改个人密码等&#xff0c;而学生则可以通过系统来选择课…
阅读更多...
干货分享：品牌如何通过社媒激发年轻人消费力？

干货分享：品牌如何通过社媒激发年轻人消费力？

随着年轻人的消费愈发理性&#xff0c;年轻人在消费时更偏向于熟人种草场景下的信任决策&#xff0c;社交媒体成为品牌吸引用户的必争之地。今天媒介盒子就来和大家聊聊&#xff1a;品牌如何通过社媒激发年轻人消费力。 一、 激发用户共鸣&#xff0c;与用户产生情感连接。 虽…
阅读更多...
Midjourney辞典AIGC中英双语图文辞典+Midjourney提示关键词

Midjourney辞典AIGC中英双语图文辞典+Midjourney提示关键词

完整内容下载&#xff1a;https://download.csdn.net/download/u010564801/89042077 完整内容下载&#xff1a;https://download.csdn.net/download/u010564801/89042077 完整内容下载&#xff1a;https://download.csdn.net/download/u010564801/89042077
阅读更多...
哈希表（hash_table） 哈希存储 算法相关知识 稳定性 时间复杂度

哈希表（hash_table） 哈希存储 算法相关知识 稳定性 时间复杂度

哈希存储(散列存储) 为了快速定位数据 哈希表 哈希冲突 / 哈希矛盾 关键字不一样&#xff0c;但是映射之后结果一样 如何避免 哈希矛盾&#xff1f; 1、重新设计哈希函数&#xff0c;尽可能均匀散列分布在哈希表 2、开放定址法&#xff1a;向下寻找未存储的位置进行存放数…
阅读更多...
aardio - 【库】godking.plusSkin 设置plus样式

aardio - 【库】godking.plusSkin 设置plus样式

库名&#xff1a;godking.plusSkin 库文件下载工具&#xff1a;http://chengxu.online/show.asp?softid272 使用本库&#xff0c;可以快速设置plus样式。主要针对按钮样式进行快速批量设置。 部分用法如下&#xff1a; import win.ui; /*DSG{{*/ var winform win.form(tex…
阅读更多...
C++初学者：如何优雅地写程序

C++初学者：如何优雅地写程序

我喜欢C语言的功能强大&#xff0c;简洁&#xff0c;我也喜欢C#的语法简单&#xff0c;清晰&#xff0c;写起来又方便好用。 一、为什么不用C语言写程序。 C语言用来做题目&#xff0c;考试研究是很方便的&#xff0c;但是用来写程序做软件&#xff0c;你就会发现&#xff0c…
阅读更多...
Android中运动事件的处理

Android中运动事件的处理

1.目录 目录 1.目录 2.前言 3.程序演示 4.第二种程序示例 5.扩展 2.前言 触摸屏&#xff08;TouchScreen&#xff09;和滚动球&#xff08;TrackBall&#xff09;是 Android 中除了键盘之外的主要输入设备。如果需要使用触摸屏和滚动球&#xff0c;主要可以通过使用运动事…
阅读更多...
[DS]Polar靶场web(一)

[DS]Polar靶场web(一)

静以养心&#xff0c;宽以养气。 跟着Dream ZHO大神学专升安的一天 swp 直接dirb扫出.index.php.swp的目录 function jiuzhe($xdmtql){return preg_match(/sys.*nb/is,$xdmtql);//如果包含以 "sys" 开始&#xff0c;后跟任意字符直到 "nb" 的字符串&…
阅读更多...
[XG] HTTP

[XG] HTTP

我希望风起&#xff0c;而你好像更希望风停。 闲来无事&#xff0c;跟着Z3r4y-CSDN博客大神学一学web吧 [NewStarCTF 2023]Begin of HTTP 1.题目要求使用GET方式来给ctf参数传入任意值&#xff0c;那就传吧。 2.又让以POST方式来传递secert参数&#xff0c;并且要找一下参数…
阅读更多...
python--字符串和常见的方法

python--字符串和常见的方法

1.字符串对象 字符串 " 字符串 " """ 字符串 """ 字符串 str() #全局函数&#xff0c;将一个类型转化为字符串 len(字符串) #获取字符串长度 while 和 for 循环&#xff0c;遍历字符串 案例一&#xff1a;查看字…
阅读更多...
ubuntu系统下如何使用vscode编译和调试#小白入门#

ubuntu系统下如何使用vscode编译和调试#小白入门#

编程环境&#xff1a;ubuntu系统为18.04.1&#xff0c;vscode版本为1.66.2 一、VSCode切换中文显示&#xff1a; 1、vscode安装完成后启动,在左侧externsions中搜索“简体中文”插件&#xff0c;并完成安装&#xff1a; 2、选择右下角齿轮形状的"Manage"&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023