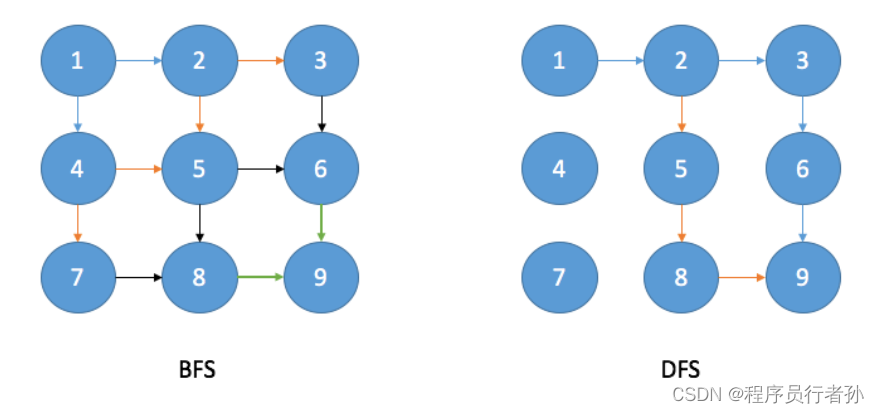
先复习一下什么是BFS和DFS,各位读者接着往下看就行
BFS算法
BFS类似于树的层次遍历过程,从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。
舍去空间换时间。
算法思路
队列(先进先出)
1、创建一个空队列queue(用来存放节点)和一个空列表visit(用来存放已访问的节点)
2、依次将起始点及邻接点加入queue和visit中
3、pop出队列中最先进入的节点,从图中获取该节点的邻接点
4、如果邻接点不在visit中,则将该邻接点加入queue和visit中
5、输出pop出的节点
6、重复3、4、5,直至队列为空
DFS算法
DFS沿着树的深度遍历树的节点,
选一条路一直走到底,回溯,遍历所有的子节点,进而达到全局搜索的目的。
算法思路
栈(先进后出)
和BFS相似,只是稍微做了一丝改变
1、创建一个空栈stack(用来存放节点)和一个空列表visit(用来存放已访问的节点)
2、依次将起始点及邻接点加入stack和visit中
3、poo出栈中最后进入的节点,从图中获取该节点的邻接点
4、如果邻接点不在visit中,则将该邻接点加入stack和visit中
5、输出pop出的节点
6、重复3、4、5,直至栈为空
接下来以LeetCode的一道经典题为背景来强化一下写法。
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1 输入:grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出:3
题目很经典的BFS和DFS都能做,遍历就行
DFS题解
我们可以将二维网格看成一个无向图,竖直或水平相邻的 1 之间有边相连。为了求出岛屿的数量,我们可以扫描整个二维网格。如果一个位置为 1,则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中,每个搜索到的 1 都会被重新标记为 0。最终岛屿的数量就是我们进行深度优先搜索的次数。
代码:
class Solution {
public:
// 深度优先搜索函数,用于将当前岛屿中所有相连的陆地标记为已访问('0')
void dfs(vector<vector<char>>& grid, int i, int j) {
int n = grid.size(); // 获取网格的行数
int m = grid[0].size(); // 获取网格的列数
grid[i][j] = '0'; // 将当前位置标记为已访问
// 检查当前位置的上、下、左、右四个方向是否有相邻的陆地,如果有,则继续深度优先搜索
if (i - 1 >= 0 && grid[i - 1][j] == '1') dfs(grid, i - 1, j); // 上
if (i + 1 < n && grid[i + 1][j] == '1') dfs(grid, i + 1, j); // 下
if (j - 1 >= 0 && grid[i][j - 1] == '1') dfs(grid, i, j - 1); // 左
if (j + 1 < m && grid[i][j + 1] == '1') dfs(grid, i, j + 1); // 右
}
// 主函数,用于计算网格中岛屿的数量
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(); // 获取网格的行数
if (!n) return 0; // 如果网格为空,则返回岛屿数量为0
int m = grid[0].size(); // 获取网格的列数
int res = 0; // 用于记录岛屿的数量
// 遍历整个网格
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 如果当前位置是陆地('1'),则进入深度优先搜索,将与之相连的所有陆地标记为已访问,并将岛屿数量加一
if (grid[i][j] == '1') {
res++; // 岛屿数量加一
dfs(grid, i, j); // 深度优先搜索,将与当前陆地相连的所有陆地标记为已访问
}
}
}
return res; // 返回岛屿的数量
}
};
BFS题解
同样地,我们也可以使用广度优先搜索代替深度优先搜索。为了求出岛屿的数量,我们可以扫描整个二维网格。如果一个位置为 1,则将其加入队列,开始进行广度优先搜索。在广度优先搜索的过程中,每个搜索到的 1 都会被重新标记为 0。直到队列为空,搜索结束。最终岛屿的数量就是我们进行广度优先搜索的次数
代码:
class Solution {
public:
// 计算岛屿数量的函数
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(); // 获取网格的行数
if (!n) return 0; // 如果网格为空,则返回岛屿数量为0
int m = grid[0].size(); // 获取网格的列数
int res = 0; // 用于记录岛屿的数量
// 遍历整个网格
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 如果当前位置是陆地('1'),则进入广度优先搜索,将与之相连的所有陆地标记为已访问,并将岛屿数量加一
if (grid[i][j] == '1') {
res++; // 岛屿数量加一
grid[i][j] = '0'; // 将当前位置标记为已访问
queue<pair<int,int>> neighbors; // 创建一个队列用于存储当前岛屿相邻的陆地
neighbors.push({i, j}); // 将当前位置加入队列
while (!neighbors.empty()) { // 循环直到队列为空
auto t = neighbors.front(); // 取出队首元素
neighbors.pop(); // 弹出队首元素
int row = t.first, col = t.second; // 获取当前位置的行和列
// 检查当前位置的上、下、左、右四个方向是否有相邻的陆地,如果有,则将其加入队列,并标记为已访问
if (row + 1 < n && grid[row + 1][col] == '1') {
neighbors.push({row + 1, col});
grid[row + 1][col] = '0';
}
if (row - 1 >= 0 && grid[row - 1][col] == '1') {
neighbors.push({row - 1, col});
grid[row - 1][col] = '0';
}
if (col + 1 < m && grid[row][col + 1] == '1') {
neighbors.push({row, col + 1});
grid[row][col + 1] = '0';
}
if (col - 1 >= 0 && grid[row][col - 1] == '1') {
neighbors.push({row, col - 1});
grid[row][col - 1] = '0';
}
}
}
}
}
return res; // 返回岛屿的数量
}
};