1 二叉树
二叉树和树都属于树形结构,但两者互不包含。即二叉树不是特殊的树。
1.1 二叉树的基本概念
1.2 二叉树的顺序存储
仅适用于完全二叉树
#define MaxSize 100
typedef int ElemType;
typedef struct TreeNode{
ElemType value;//结点中的数据元素
bool isEmpty;//结点是否为空
}TreeNode;构造结点数为MaxSize的完全二叉树t。
TreeNode t[MaxSize];1.3 二叉树的链式存储
1.3.1 二叉链表
typedef struct BiNode{
ElemType data;//数据域
struct BiNode *lchild,*rchild;//左右孩子指针
}BiNode,*BiTree; 二叉链表具体实现:
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
typedef char ElemType;
//二叉树的结点(链式存储)
typedef struct BiNode{
ElemType data;//数据域
struct BiNode *lchild,*rchild;//左右孩子指针
// struct BiTNode *parent;//父节点指针 三叉链表
}BiNode,*BiTree;
//先序遍历的顺序建立二叉链表
void CreateBiTree(BiTree &T){
char ch;
cin>>ch;
if(ch=='#') T=NULL;
else{
T=new BiNode;
T->data=ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
}
//先序遍历
void PreOrder(BiTree T){
if(T!=NULL){
cout<<T->data<<" ";
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
//中序遍历
void InOrder(BiTree T){
if(T!=NULL){
PreOrder(T->lchild);
cout<<T->data<<" ";
PreOrder(T->rchild);
}
}
//后序遍历
void AfterOrder(BiTree T){
if(T!=NULL){
PreOrder(T->lchild);
PreOrder(T->rchild);
cout<<T->data<<" ";
}
}
//非递归调用的先序遍历
void PreOrderTree(BiTree T){
stack<BiNode *> s;
while(T||!s.empty()){
while(T){
cout<<T->data;
s.push(T);
T=T->lchild;
}
if(!s.empty()){
T=s.top();
s.pop();
T=T->rchild;
}
}
cout<<endl;
}
//非递归调用的中序遍历
void InOrderTree(BiTree T){
stack<BiNode *> s;
while(T||!s.empty()){
while(T){
s.push(T);
T=T->lchild;
}
if(!s.empty()){
T=s.top();
s.pop();
cout<<T->data;
T=T->rchild;
}
}
cout<<endl;
}
//非递归调用的后序遍历
void AfterOrderTree(BiTree T){
stack<BiNode*> s;
BiNode* lastVisited = NULL; // 记录上一个访问过的结点
while (T || !s.empty()) {
while (T) {
s.push(T);
T = T->lchild;
}
if (!s.empty()) {
BiNode* topNode = s.top();
if (topNode->rchild && topNode->rchild != lastVisited) {
T = topNode->rchild;
} else {
cout << topNode->data;
lastVisited = topNode;
s.pop();
}
}
}
cout << endl;
}
//层次遍历
void LevelOrder(BiTree T){
queue<BiNode *> q;
q.push(T);
while(q.size()){
BiNode *f=q.front();
q.pop();
cout<<f->data;
if(f->lchild!=NULL){
q.push(f->lchild);
}
if(f->rchild!=NULL){
q.push(f->rchild);
}
}
cout<<endl;
}
//复制二叉树
void Copy(BiTree T,BiTree &NewT){
if(T==NULL){
NewT=NULL;
return;
}else{
NewT=new BiNode;
NewT->data=T->data;
Copy(T->lchild,NewT->lchild);
Copy(T->rchild,NewT->rchild);
}
}
//计算二叉树的深度
int Depth(BiTree T){
if(T==NULL){
return 0;
}
int m=Depth(T->lchild);
int n=Depth(T->rchild);
if(m>n){
return m+1;
}else{
return n+1;
}
}
//统计二叉树中结点的个数
int NodeCount(BiTree T){
if(T==NULL) return 0;
else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}
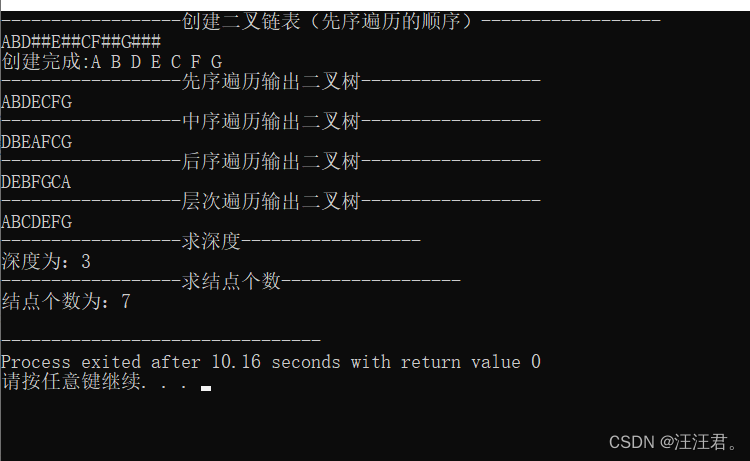
int main(){
BiTree T;
cout<<"------------------创建二叉链表(先序遍历的顺序)------------------"<<endl;
CreateBiTree(T);
cout<<"创建完成:";
PreOrder(T);//先序遍历的顺序输出二叉树
cout<<endl;
cout<<"------------------先序遍历输出二叉树------------------"<<endl;
PreOrderTree(T);
cout<<"------------------中序遍历输出二叉树------------------"<<endl;
InOrderTree(T);
cout<<"------------------后序遍历输出二叉树------------------"<<endl;
AfterOrderTree(T);
cout<<"------------------层次遍历输出二叉树------------------"<<endl;
LevelOrder(T);
cout<<"------------------求深度------------------"<<endl;
cout<<"深度为:"<<Depth(T)<<endl;
cout<<"------------------求结点个数------------------"<<endl;
cout<<"结点个数为:"<<NodeCount(T)<<endl;
return 0;
} 
求中序遍历的前驱和后继:
//找前驱
BiNode *p;//目标结点
BiNode *pre;
BiNode *final;
void visit(BiNode *q){
if(q==p){
final=pre;
}else{
pre=q;
}
// //找后继
// if(pre==p){
// final=q;
// }else{
// pre=q;
// }
}
void findPre(BiTree T){
if(T!=NULL){
T=T->lchild;
visit(T);
T=T->rchild;
}
} 1.3.2 线索链表
定义
typedef char ElemType;
typedef struct BiThrNode{
ElemType data;
struct BiThrNode *lchild,*rchild;
int LTag,RTag;//左右标志,0:指向左右孩子 1:指向前驱或后继
}BiThrNode,* BiThrTree; 先序线索化
//先序线索化(防止转圈问题)
void PreThreadTree(BiThrNode *p,BiThrNode *pre){
if(p!=NULL){
//根
if(p->lchild==NULL){
p->LTag=1;
p->lchild=pre;
}else{
p->LTag=0;
}
if(pre!=NULL&&pre->rchild==NULL){
pre->RTag=0;
pre->rchild=p;
}else{
p->RTag=0;
}
pre=p;
//左
if(p->LTag==0) PreThreadTree(p->lchild,pre);
//右
PreThreadTree(p->rchild,pre);
}
}
void CreatePreThreadTree(BiThrTree T){
BiThrNode *pre=NULL;
if(T!=NULL){
InThreadTree(T,pre);
if(pre->rchild==NULL){
pre->RTag=1;
}
}
}中序线索化
//中序线索化
void InThreadTree(BiThrNode *p,BiThrNode *pre){
if(p!=NULL){
InThreadTree(p->lchild,pre);
if(p->lchild==NULL){
p->LTag=1;
p->lchild=pre;
}else{
p->LTag=0;
}
if(pre!=NULL&&pre->rchild==NULL){
pre->RTag=0;
pre->rchild=p;
}else{
p->RTag=0;
}
pre=p;
InThreadTree(p->rchild,pre);
}
}
void CreateInThreadTree(BiThrTree T){
BiThrNode *pre=NULL;
if(T!=NULL){
InThreadTree(T,pre);
if(pre->rchild==NULL){
pre->RTag=1;
}
}
}后序线索化
//后序线索化
void PostThreadTree(BiThrTree p,BiThrNode *pre){
if(p!=NULL){
//左
PostThreadTree(p->lchild,pre);
//右
PostThreadTree(p->rchild,pre);
//根
if(p->lchild==NULL){
p->LTag=1;
p->lchild=pre;
}else{
p->LTag=0;
}
if(pre!=NULL&&pre->rchild==NULL){
pre->RTag=0;
pre->rchild=p;
}else{
p->RTag=0;
}
pre=p;
}
}
void CreatePostThreadTree(BiThrTree T){
BiThrNode *pre=NULL;
if(T!=NULL){
InThreadTree(T,pre);
if(pre->rchild==NULL){
pre->RTag=1;
}
}
} 1.3.3 三叉链表
typedef struct BiNode{
ElemType data;//数据域
struct BiNode *lchild,*rchild;//左右孩子指针
struct BiTNode *parent;//父节点指针
}BiNode,*BiTree;2 树
1.1 树的基本概念
树(Tree)是n(n>=0)个结点的有限集,它或为空树(n=0);或为非空树。
基本术语
结点:树中的一个独立单元