【数据结构】计数排序

news2024/12/25 9:20:04

大家好，我是苏貝，本篇博客带大家了解计数排序，如果你觉得我写的还不错的话，可以给我一个赞👍吗，感谢❤️

一. 基本思想

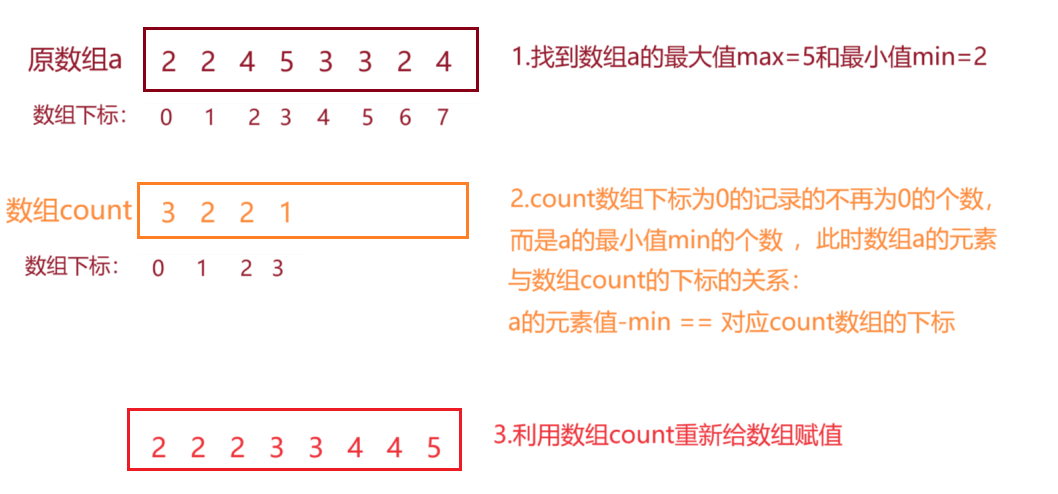
计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。操作步骤：

统计相同元素出现次数
根据统计的结果将序列回收到原来的序列中

在这里插入图片描述

发现了吗？计数排序和我们之前介绍的7个排序都不同，它不需要让数组a中的元素相互比较，所以它是非比较排序。可想而知，如果有一个数组的所有的值相差不大，那计数排序的效率是非常高的。

按照上面的思想，数组count的下标都从0开始的话，如果数组a为{1000，1111，1222，1333，1444，…，2000}，那么我们要开辟count数组，数组下标从0开始到2000结束，前1000个空间都被浪费了，所以我们还可以改进一下。这种方法叫相对映射，上面的叫绝对映射

在这里插入图片描述

二. 计数排序代码

了解了计数排序的思想，现在我们来想想代码应该怎么写

1.遍历数组a，找到最大值max和最小值min。
这样我们就能知道数组a的元素范围range，动态开辟有range个元素的数组count，为了方便，我们用calloc函数开辟，这样count的每个元素的初始值都为0

2.再遍历数组a，记录每个元素的个数。
每遇见一个元素a[i]，都让count[ a[ i ] -min]++，其中 a[ i ] -min是a[i]对应count数组的下标

3.遍历count数组，count[i]=n，就让数组a里有n个元素（i+min）

void CountSort(int* a, int n)
{
	//1.找到最大值max和最小值min
	int min = a[0], max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];
		if (a[i] > max)
			max = a[i];
	}

	//2.动态开辟有range个元素的数组count
	int range = max - min + 1;
	int* count = (int*)calloc(range, sizeof(int));
	if (count == NULL)
	{
		perror("calloc fail");
		return;
	}

	//3.记录每个元素的个数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

	//4.利用数组count重新给数组a赋值
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}

下面我们来验证一下，如果数据范围集中的话，计数排序的效率是否真的很高。我们用rand函数生成100万个随机数，看看各排序的效率（只能生成3万多个随机数，其它将近997万个随机数都是重复的）

void TestOP()
{
	srand(time(0));
	const int N = 1000000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
	}

	int begin1 = clock();
	ShellSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	HeapSort(a2, N);	
	int end2 = clock();

	int begin3 = clock();
	QuickSort1(a3, 0, N - 1);
	int end3 = clock();

	int begin4 = clock();
	MergeSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	CountSort(a5, N);
	int end5 = clock();

	printf("ShellSort:%d\n", end1 - begin1);
	printf("HeapSort:%d\n", end2 - begin2);
	printf("QuickSort1:%d\n", end3 - begin3);
	printf("MergeSort:%d\n", end4 - begin4);
	printf("CountSort:%d\n", end5 - begin5);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
}