R 生存分析3：Cox等比例风险回归及等比例风险检验

虽然Kaplan-Meier分析方法目前应用很广，但是该方法存在一下局限:

对于一些连续型变量，必须分类下可以进行生存率对比
是一种单变量分析，无法同时对多组变量进行分析
是一种非参数分析方法，必须有患者个体数据才能进行分析

英国统计学家David Cox在1972年进一步拓展了Kaplan-Meier，将性别和年龄等因素包含在内，也就是Cox Proportional Hazard Model（Cox回归），该方法可以用来预测一个或多个不同变量在某一时间对死亡率的影响。它同时适用于数值变量和类别变量，可以同时评估几种风险因素对生存时间的影响，检验特定因素如何影响特定时间点特定事件（例如，感染，死亡）的发生率因此广泛应用于生物医学的统计和分析。

(Remembering Sir David Cox, 1924–2022)

值得注意的是Cox回归的是一种半参数法，其分布本身同样也不含参数假设，只是性别、年龄等影响因素对生存概率的影响是用参数来表达的。本文主要内容是对COX回归及该方法使用前提等比例风险假设进行介绍，具体包括以下内容：

COX回归的原理及假设
如何在R语言中实现单变量COX回归
如何在R语言中实现多变量COX回归
绘制森林图展示多变量COX回归结果
如何在R语言中对生存数据进行等比例风险检验

2.原理及假设

在生存分析文献中，预测变量（或因子）通常称为协变量，发生率被称为风险率。Cox 模型核心是由h（t）表示的危险函数，可理解为在时间 t 死亡的风险，其模型算法如下：

在上述模型中称为基线风险函数，与其他形式的回归一样存在β项乘以每个预测变量。由于基线风险表示协变量值均为 0 或处于参考水平的个体的风险，所以类似于线性回归模型中的截距。另外由于基线风险函数不依赖于任何参数，并且在估计模型参数时完全消失，因此，Cox 回归输出不包括截距。在上述模型中， β 表示风险比（hazard ratio，HR），HR> 1的协变量被称为不良预后因素；HR<1的协变量被称为良好的预后因子。

目前风险比（HR）通常用于报告肿瘤学随机临床试验的结果。在肿瘤学随机临床试验（RCT）中，经常使用风险比（HR）来估计至事件发生时间终点的治疗效果，如总生存期（OS）和无进展生存期（PFS）。HR提供了整个研究期间试验组和对照组之间风险率比值的估计值，例如OS终点的HR = 0.75，意味着试验组的死亡风险相比对照组降低约25%。

3. COX回归R语言实现

本文依然采用上篇研究中的bladder1 数据集进行分析，采用患者复发作为关注的事件：

library(tidyverse)
library(survival)
library(survminer)
data(cancer, package="survival")

bladder1 <-
  bladder1 %>% 
  mutate(recurr = if_else(status == 1, 1, 0),
         time = stop - start,
         rtumor = as.numeric(na_if(rtumor, ".")),
         rsize = as.numeric(na_if(rsize, "."))) %>% 
  filter(start == 0)

单变量COX回归

使用coxph函数对干预措施进行单变量COX回归:

bladder1.cox.1 <- coxph(Surv(time, recurr) ~ treatment, data = bladder1)
summary(bladder1.cox.1)

Call:
coxph(formula = Surv(time, recurr) ~ treatment, data = bladder1)

  n= 118, number of events= 62 

                       coef exp(coef) se(coef)      z
treatmentpyridoxine -0.3532    0.7024   0.3202 -1.103
treatmentthiotepa   -0.3830    0.6818   0.3025 -1.266
                    Pr(>|z|)
treatmentpyridoxine    0.270
treatmentthiotepa      0.205

                    exp(coef) exp(-coef) lower .95
treatmentpyridoxine    0.7024      1.424    0.3750
treatmentthiotepa      0.6818      1.467    0.3769
                    upper .95
treatmentpyridoxine     1.316
treatmentthiotepa       1.234

Concordance= 0.533  (se = 0.038 )
Likelihood ratio test= 2.05  on 2 df,   p=0.4
Wald test            = 2.07  on 2 df,   p=0.4
Score (logrank) test = 2.09  on 2 df,   p=0.4

通过HR的置信区间和P值可以看出三种干预措施对减少患者转移风险上没有统计学差异。

2. 多变量COX回归

使用coxph函数对所有变量进行多变量COX回归

bladder1.cox.2 <- coxph(Surv(time, recurr) ~ treatment + number + size, data = bladder1)
summary(bladder1.cox.2)

Call:
coxph(formula = Surv(time, recurr) ~ treatment + number + size, 
    data = bladder1)

  n= 118, number of events= 62 

                        coef exp(coef) se(coef)      z
treatmentpyridoxine -0.34130   0.71085  0.32227 -1.059
treatmentthiotepa   -0.55105   0.57634  0.31257 -1.763
number               0.25249   1.28723  0.06498  3.886
size                 0.05892   1.06069  0.07414  0.795
                    Pr(>|z|)    
treatmentpyridoxine 0.289585    
treatmentthiotepa   0.077904 .  
number              0.000102 ***
size                0.426761    
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

                    exp(coef) exp(-coef) lower .95
treatmentpyridoxine    0.7108     1.4068    0.3780
treatmentthiotepa      0.5763     1.7351    0.3123
number                 1.2872     0.7769    1.1333
size                   1.0607     0.9428    0.9172
                    upper .95
treatmentpyridoxine     1.337
treatmentthiotepa       1.064
number                  1.462
size                    1.227

Concordance= 0.642  (se = 0.038 )
Likelihood ratio test= 14.94  on 4 df,   p=0.005
Wald test            = 16.55  on 4 df,   p=0.002
Score (logrank) test = 17.75  on 4 df,   p=0.001

多变量COX回归结果显示，初始肿瘤数量增加了风险，因此预后更差。

3. 森林图（forest plot）绘制

使用ggforest函数对回归结果进行森林图绘制

ggforest(bladder1.cox.2, data = bladder1)

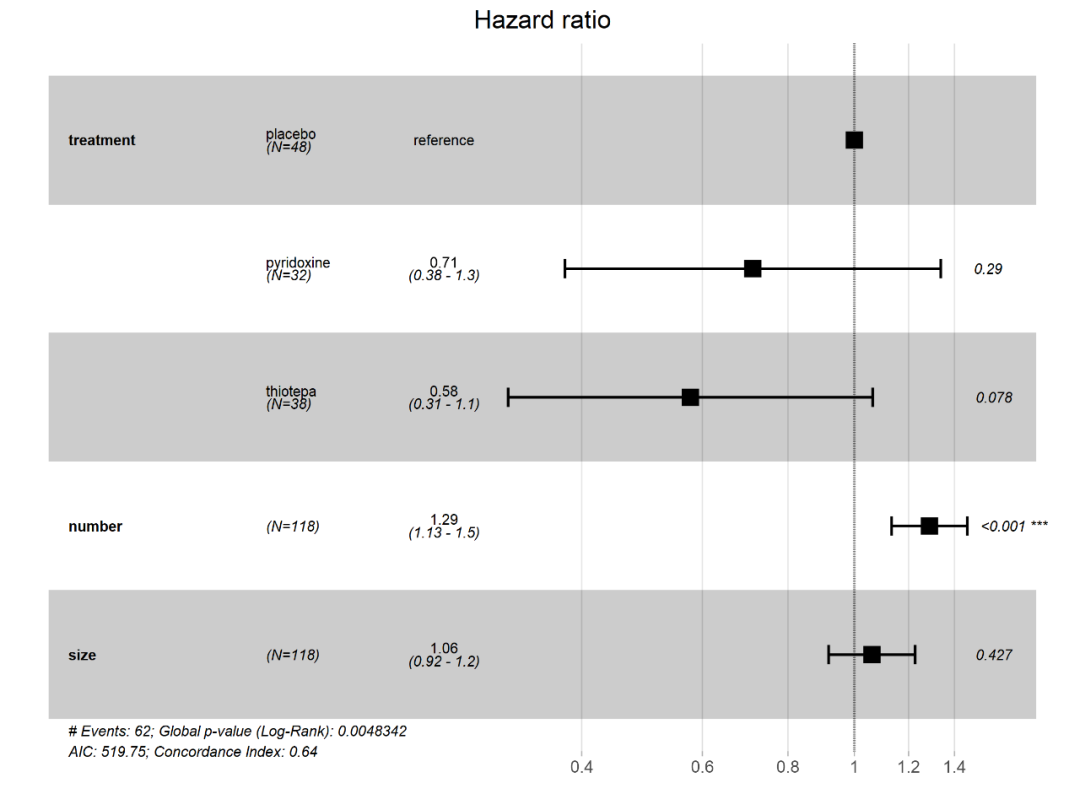
4. 等比例风险检验R语言实现

等比例风险（PH）：在任意一个时间点，两组人群发生时间的风险比例是恒定的；或者说其危险曲线应该是成比例而且是不能交叉的；也就是如果一个体在某个时间点的死亡风险是另外一个体的两倍，那么在其他任意时间点的死亡风险也同样是2倍，但是有时在研究过程中会遇到延迟反应、假性进展，从而导致生存曲线（如PFS）早期就纠缠在一起，几个月后才分开，这时Cox模型的假设就不成立了。

在进行COX回归前，通常需要进行以下三种检验：

使用Schoenfeld residuals 检查等比例风险（proportional hazards）；
使用Deviance residual 检查异常值（outliers）;
使用Martingale residual检查风险与协变量之间的非线性关系（ non-linearity）

使用Schoenfeld residuals进行等比例风险检验

test.ph.2 <- cox.zph(bladder1.cox.2)
print(test.ph.2)

           chisq df    p
treatment 1.0940  2 0.58
number    0.0865  1 0.77
size      1.1794  1 0.28
GLOBAL    2.4600  4 0.65

从上述输出来看，对每个协变量的检验都没有统计学意义，而全局检验也没有统计学差异,因此，我们可以假设成比例的风险。同时可以使用ggcoxzph函数绘制各变量scaled Schoenfeld residuals残差图。

ggcoxzph(test.ph.2)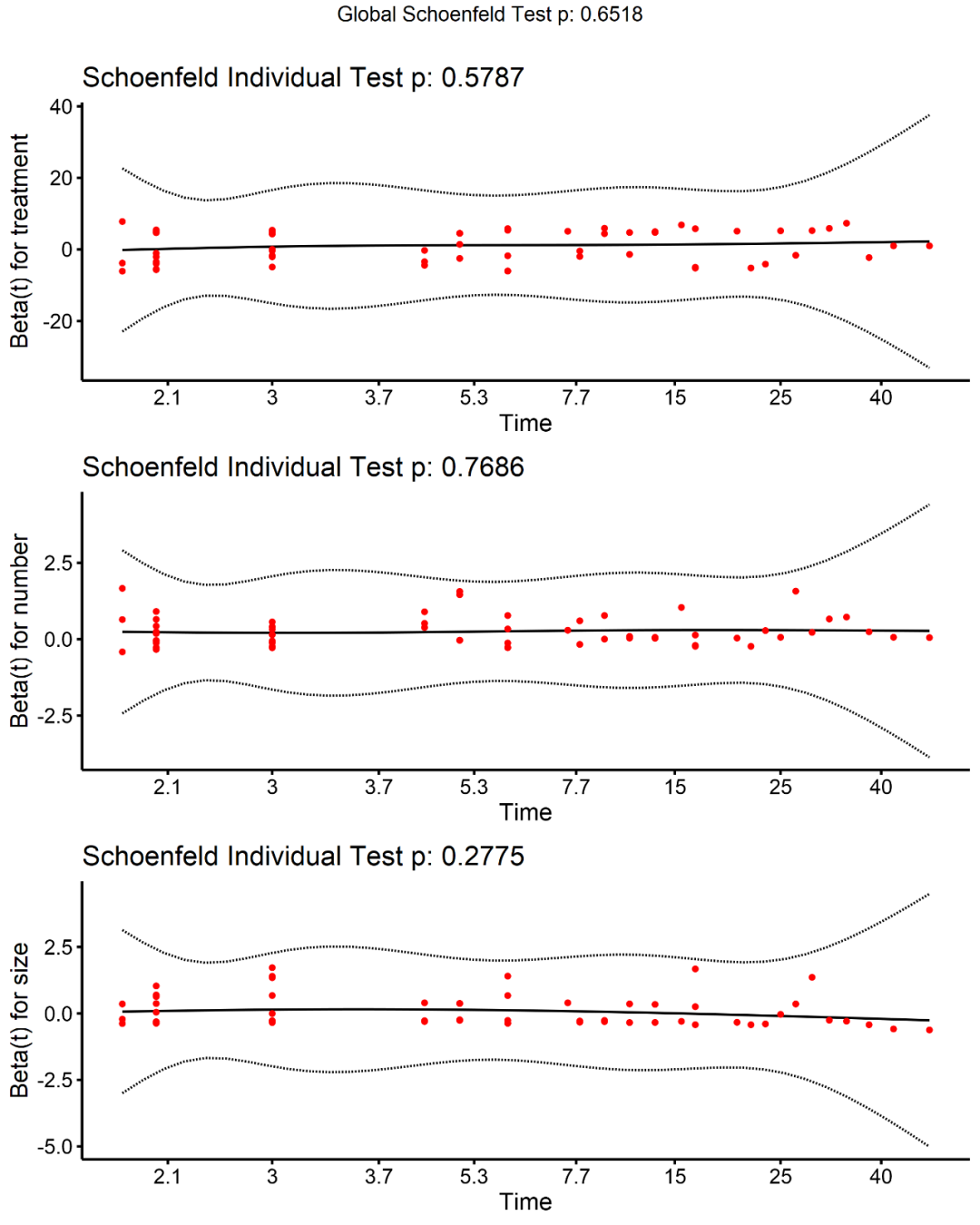

如果图片中的红点系统偏离水平线则表明存在非等比例风险，而等比例风险假设估计值不会随时间变化很大。

2.使用deviance残差图检测是否有异常值

可通过ggcoxdiagnostics函数展示deviance residuals或者dfbeta values图形来检查异常值。其中type指y轴展示的误差项，c(“martingale”, “deviance”, “score”, “schoenfeld”, “dfbeta”, “dfbetas”, “scaledsch”, “partial”)

ggcoxdiagnostics(
  bladder1.cox.2,
  type = "dfbeta"
)

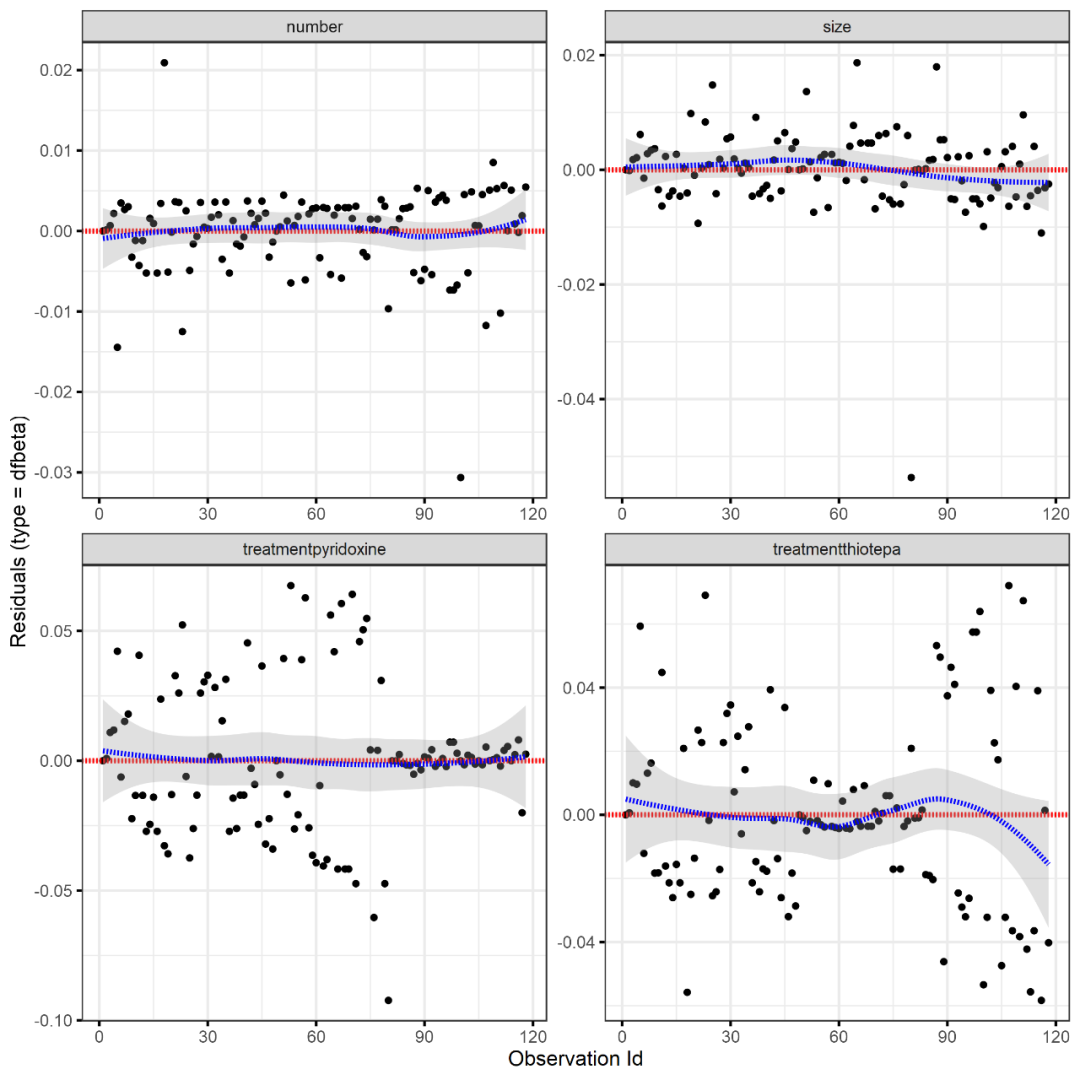
上述图片展示了删除每个观察结果后回归系数的估计变化，上面的图片表明，没有一个观察结果本身有特别的影响。

3.使用Martingale residual检测非线性关系

通过绘制Martingale残差与协变量的散点图来检验非线性。

ggcoxfunctional(Surv(time, recurr) ~  number + log(number) + sqrt(number), 
data = bladder1)

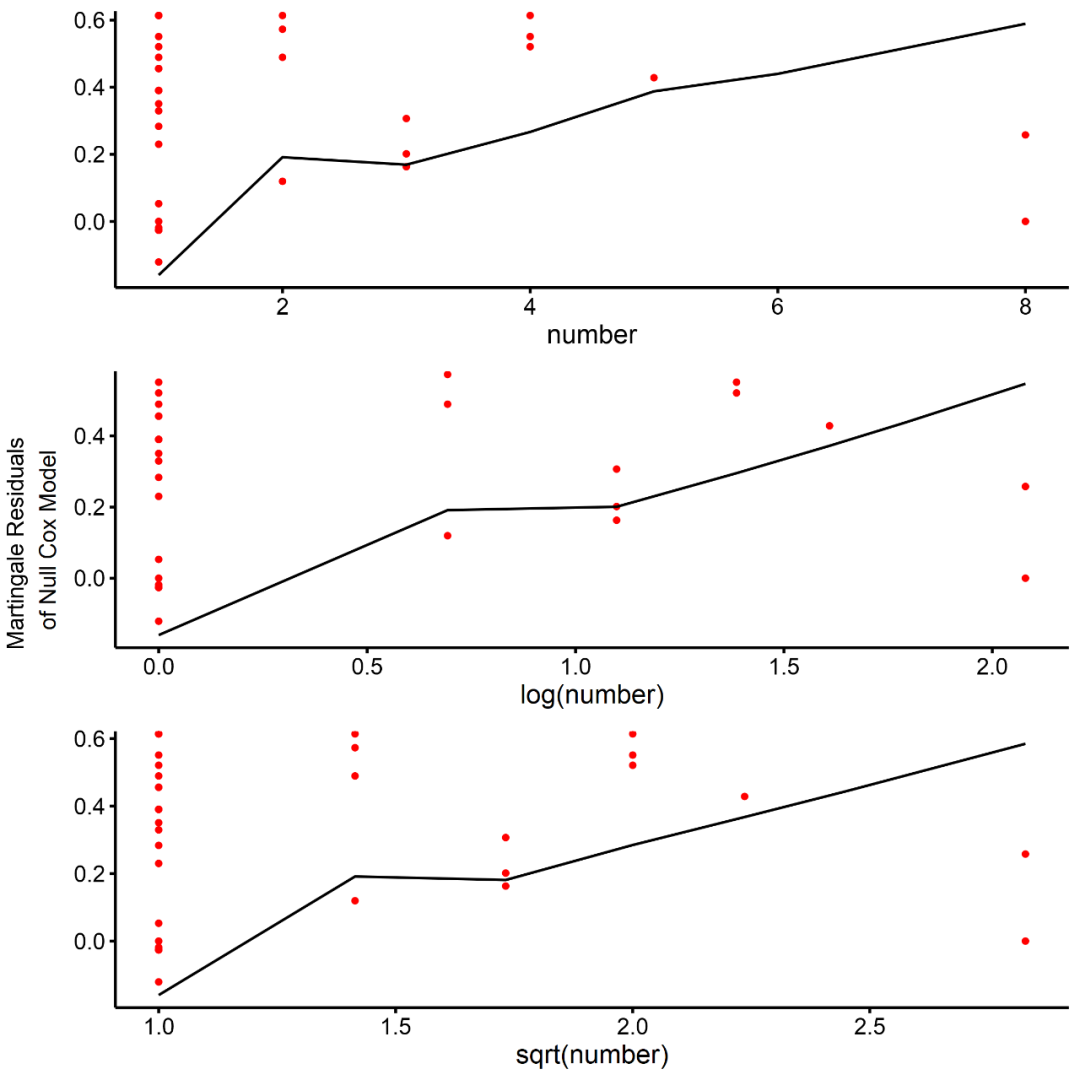
上述图片显示了连续协变量与cox比例风险模型的残差的关系，上图表示初始肿瘤数量有轻微的非线性。

5. 优点和局限

相较于K-M分析，COX回归方法存在以下优点：首先，HR囊括了整个KM生存曲线中的所有信息，因此总结了RCT整个持续时间内的治疗效果。相比之下，中位生存期仅关注治疗组生存曲线上的一个点，最多代表“组平均年龄”，作为个体患者疾病控制持续时间或OS的指标过于简单。其次，HR提供了治疗组之间相对疗效的估计值（例如，OS终点的HR = 0.75，意味着试验组的死亡风险相比对照组降低约25%）。

但是该方法运用的前提是等比例风险（PH）假设：研究期间每个时间间隔的风险率比值近似恒定。因而如果生存数据严重违反等比例风险假设，则该方法的结果便难以解释，此时需要采用其他方法进行分析（后续文章更新）：