谱峭度SK的本质是计算每根谱线峭度值的高阶统计量，谱峭度对信号中的瞬态冲击成分十分敏感，能有效的从含有背景噪声信号中识别瞬态冲击及其在频带中的分布。由于谱峭度的复杂性、缺少一个正式的定义和一个容易理解的计算过程使其在很长时间内都未能引入到工程应用中，直到Antoni为谱峭度做了详细的定义，并提出了基于短时傅里叶变换的SK估计器，将理论概念与实际应用联系起来，提出了Kurtogram算法，并阐述了该算法在旋转机械故障特征提取领域的具体应用过程。

为了简化Kurtogram的操作过程，提高算法的处理效率，使其满足实际工业监测的要求，Antoni又提出了快速谱峭度的概念作为Kurtogram的快速算法应用于解决非平稳信号。Kurtogram能够通过检测和表征信号的非平稳性，自适应的选择最佳带通滤波频带作为包络谱分析的前置处理。其过程是在整个频带平面内搜索频率/频率分辨率组合的最优解，从而确定瞬态冲击成分的频带位置和区间。该算法的第一层将信号分解为二叉树结构，第二层将信号分解为1/3树结构，其余的由类推得到。

众多学者对Kurtogram算法进行了改进，这些改进主要针对算法的两个方面，一方面是提升频带分割能力，通过选择优异的频带划分方法使得频率/频率分辨率趋于最优解，从而更加准确地识别和判定循环冲击成分所处于的共振频带及带宽。另一方面是改进累积统计量计算指标，用以取代峭度，从而克服峭度指标在处理某些问题时的局限性。比如为了提升频带划分精度，可以利用二进制小波包分解代替传统Kurtogram算法中的傅里叶分解和FIR滤波器。基于小波包变换的滤波器能够有效滤除噪声，精准匹配含噪声信号中故障特征区间。考虑到对时域信号计算峭度对低信噪比和存在非高斯噪声干扰时的局限性，还可以对基于小波包划分的谱峭度图算法做进一步的改进，计算各小波包子带包络信号的功率谱峭度作为统计指标的改进谱峭度图。还可以采用小波包分解作为频带划分算法，通过计算不同层度的小波包系数包络信号的功率谱稀疏度作为统计指标构建稀疏图，通过检查从所有小波包节点获得的小波包系数的最大稀疏值，可以选择最佳的小波包节点，从而确定最优频带区间。此外可以利用包络谱相关峭度代替传统的时域峭度作为统计指标，针对小波包变换中节点与频带对应关系中的频率折叠问题采用频率排序方法，进而修正小波包划分频带方法。

Antoni大佬在2016年将熵的概念引入到对Kurtogram算法的改进中，综合考虑振动信号序列中存在的冲击成分和周期性成分，提出了众多改进算法，基于Antoni变革性的理论基础，众多学者展开了对谱峭度算法的改进。比如利用多尺度聚类方法，将两个负熵进行灰度组合，同时考虑时域和频域的谱负熵，同时兼顾了信号序列中的冲击成分和周期成分。

鉴于此，提出一种新的类谱峭度算法的旋转机械故障诊断模型，该算法以较低的参数调整实现了自适应滤波频带搜索，运行环境为Python。

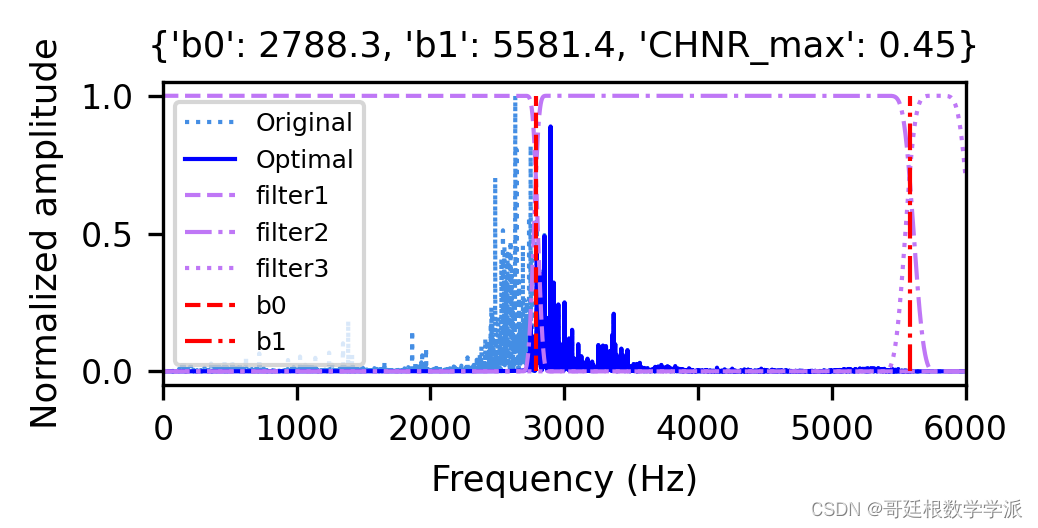
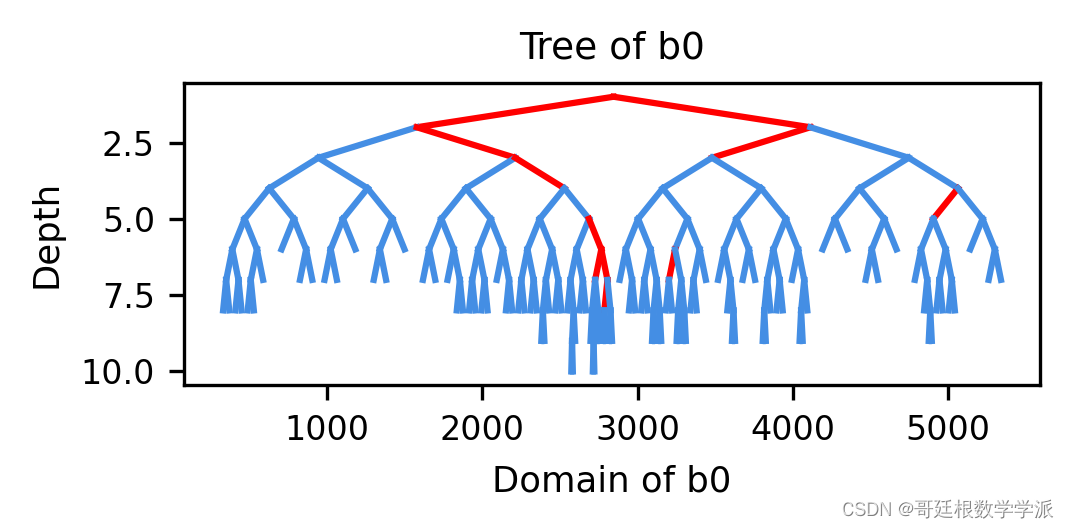
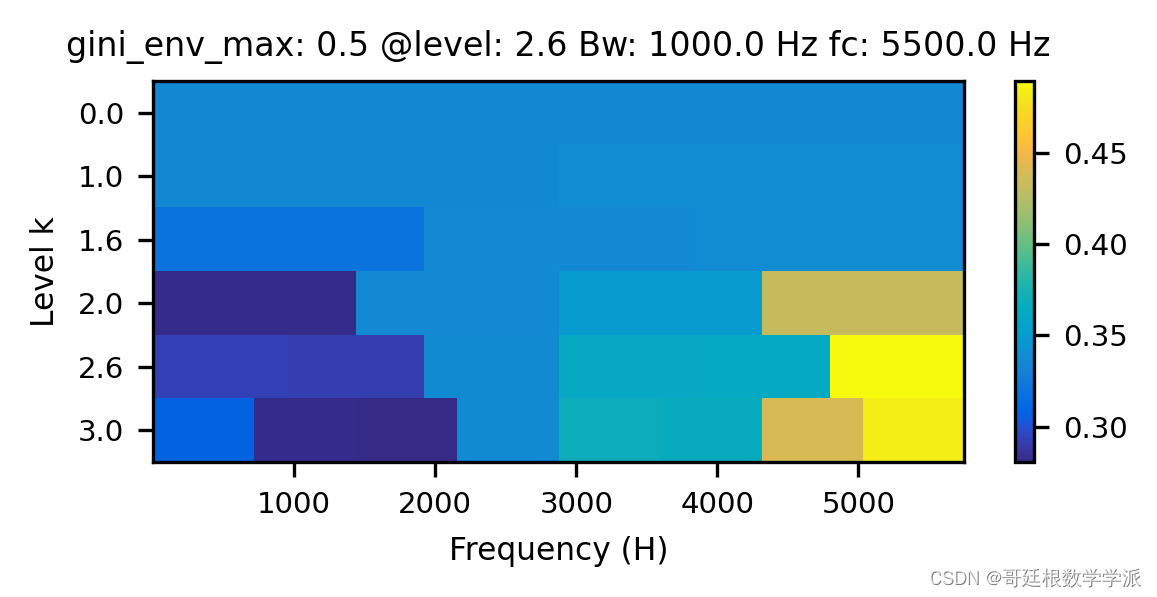
完整代码可由知乎学术咨询获得：

Python环境下一种新的类谱峭度算法的旋转机械故障诊断模型

工学博士，担任《Mechanical System and Signal Processing》审稿专家，担任《中国电机工程学报》优秀审稿专家，《控制与决策》，《系统工程与电子技术》，《电力系统保护与控制》，《宇航学报》等EI期刊审稿专家。

擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。