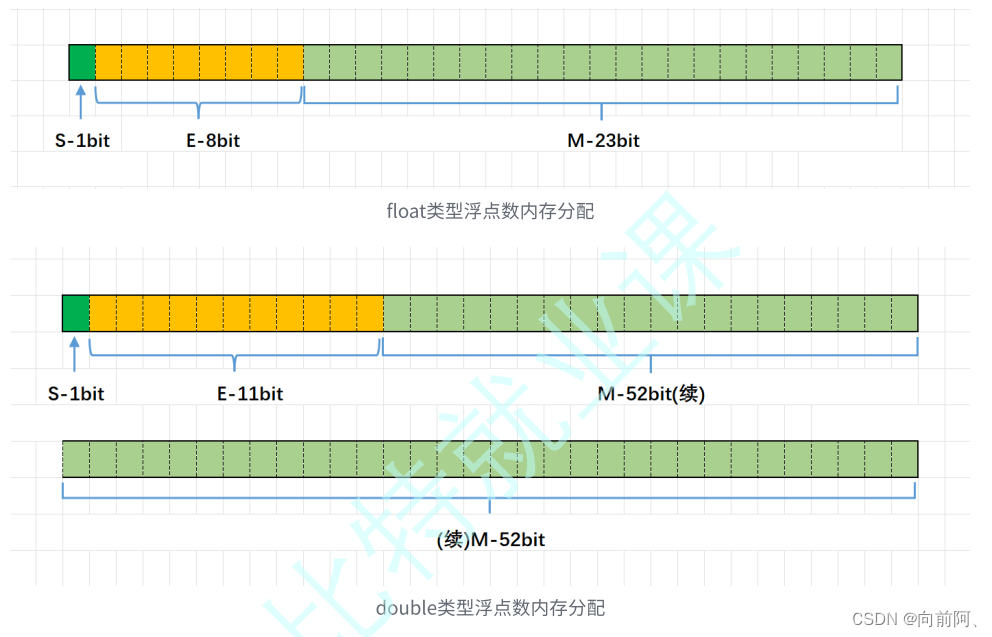
KMP:
最浅显易懂的 KMP 算法讲解_哔哩哔哩_bilibili
该视频使用python书写代码,不会python的小伙伴也可以看看了解kmp的大致思路。
问题描述:
kmp:字符串匹配算法,用来找一个长字符串中出现了几次小字符串,并找到小字符串开始的位置
1.暴力匹配:
#include<iostream>
using namespace std;
const int N=100010,M=1000010;
int n,m;// n表示小字符串的长度,m表示长字符串的长度
char p[N],s[M];//p表示小字符串,s表示大字符串
int main()
{
cin>>n>>p;
cin>>m>>s;
for(int i=0;i<m;i++)
{
int t=i;
int flag=1;
for(int j=0;j<n;j++)
{
if(s[i++]!=p[j])
{
flag=0;
break;
}
}
if(flag) cout<<i-n<<' ';
i=t;
}
return 0;
}2.kmp基本思路:(视频01:41)
当发现某一个字符串不匹配时由于已经知道之前遍历过的字符,那么我们就利用这些信息来避免暴力算法中的“回退”步骤 => 不希望 i 递减(i=t 操作)
3.kmp算法中next数组的功能(视频02:37)
在匹配失败时,会看最后一个与长字符串匹配的字符的数值:next [ j-1 ],比如next [ j-1 ]=2,则直接跳过子串的前2个字符 => 2表示可以“跳过匹配”的字符个数
4.程序实现:
#include<iostream>
using namespace std;
const int N = 100010, M = 1000010;
int n, m;//n为子长,m为母长
char p[N], s[M];//p为子串,s为母串
int ne[N];
int main()
{
cin >> n >> p + 1 >> m >> s + 1;
//求next数组的过程
//ne的第一的数为0,则i从2开始,i表示开始存哪个数的ne,j表示有多少个相同的字符,p[j+1]表示将和ne[i]匹配的字符
for (int i = 2, j = 0; i <= n; i++)
{
while (j && p[i] != p[j + 1]) j = ne[(j + 1) - 1];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
//KMP匹配过程
for (int i = 1, j = 0; i <= m; i++)//i遍历母串,j+1遍历子串,j表示要跳过几个字符
{
while (j && p[j + 1] != s[i]) j = ne[(j + 1) - 1];//j没有退回起点,且当前的s[ i ]不能和p[j+1]的位置匹配=》更新要跳过的字符
if (p[j + 1] == s[i]) j++;//匹配,则检查下一个字符
if (j == n)//匹配成功
{
printf("%d ", i - n);
j = ne[j];
}
}
return 0;
}
trie:
1.概念:
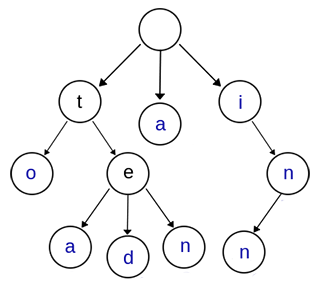
Trie树,又叫字典树、前缀树(Prefix Tree)、单词查找树 或 键树,是一种多叉树结构。如下图:
一棵Trie树,表示了关键字集合{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”} 。
作用:快速储存和查找字符串集合的数据结构
2.代码实现:
创建树,询问树
#include<iostream>
using namespace std;
const int N = 100010;
int son[N][26];//每个子节点最多连26个字母
int cnt[N];//以当前字母为结点的单词有多少个
int idx;//当前用到了那个下标,下标是0的点,既是根节点,又是空节点(给整棵树的每个结点赋予一个全局唯一的编号)
char str[N];
void insert(char str[])
{
int p = 0;
for (int i = 0; str[i]; i++)
{
int u = str[i] - 'a';
if (!son[p][u]) son[p][u] = ++idx;//头结点p的儿子中是否有26个字母中的u,没有就新建一个儿子,给他一个id(x)
p = son[p][u];//更新根节点
}
cnt[p]++;//以该结点为结尾的字符串多了一个
}
int query(char str[])
{
int p = 0;
for (int i = 0; str[i]; i++)
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
int main()
{
int n;
cin >> n;
while (n--)
{
char op[2];
cin >> op >> str;
if (op[0] == 'I') insert(str);
else cout << query(str) << endl;
}
return 0;
}