难度:中等
题目:
给定两个以 升序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v) ,其中第一个元素来自 nums1 ,第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u1,v1) , (u2,v2) ... (uk,vk) 。
示例 1:
输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数:
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
示例 2:
输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释: 返回序列中的前 2 对数:
[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]
示例 3:
输入: nums1 = [1,2], nums2 = [3], k = 3
输出: [1,3],[2,3]
解释: 也可能序列中所有的数对都被返回:[1,3],[2,3]
提示:
1 <= nums1.length, nums2.length <= 105
-109 <= nums1[i], nums2[i] <= 109
nums1 和 nums2 均为升序排列
1 <= k <= 1000
Related Topics
数组
堆(优先队列)
重点!!!解题思路
第一步:
求集合最值问题均可使用堆(优先队列)来解决
由于题中要求求出最小的k个数对
故可采用大顶堆来解决此题
第二步:
将给定的两个数组来重组一下,数组中相加的值存在大顶堆中
第三步:
最后将堆中的值转化为二维数组的方式来输出即可
源码+讲解:
class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<int[]> priorityQueue = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o2[2]-o1[2];//数组中第三位为重组数组的两个值的和
}
});
for (int i=0;i<nums1.length;i++){
for (int j=0;j<nums2.length;j++){
if (priorityQueue.size()<k ||(nums1[i]+nums2[j])<priorityQueue.peek()[2]){//比堆顶元素小才能进入堆中,这样可以少运算几次
priorityQueue.offer(new int[]{nums1[i],nums2[j],nums1[i]+nums2[j]});
if (priorityQueue.size()>k) priorityQueue.poll();
}else break;//这一步是因为两个给定数组都是升序排列,如果有一个和比堆顶大,那么后续就不用进行运算了,加快程序速度
}
}
List<List<Integer>> result = new ArrayList<>();
while (!priorityQueue.isEmpty()){
int[] ints = priorityQueue.poll();
result.add(new ArrayList<Integer>(){{
this.add(ints[0]);
this.add(ints[1]);
}});
}
return result;
}
}运行结果:
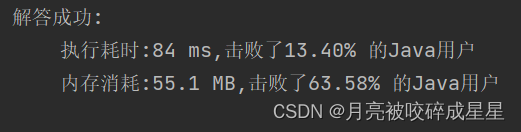
如果您还有什么疑问或解答有问题,可在下方评论,我会及时回复。
系列持续更新中,点个订阅吧